Содержание
- 2. Содержание: 1. Определение вневписанной окружности. Основные теоремы и формулы. Определение вневписанной окружности. Центр вневписанной окружности. Касательная
- 3. 1. Определение вневписанной окружности. Основные теоремы и формулы.
- 4. Вневписанная окружность. Окружность называется вневписанной для треугольника, если она касается одной стороны треугольника и продолжений двух
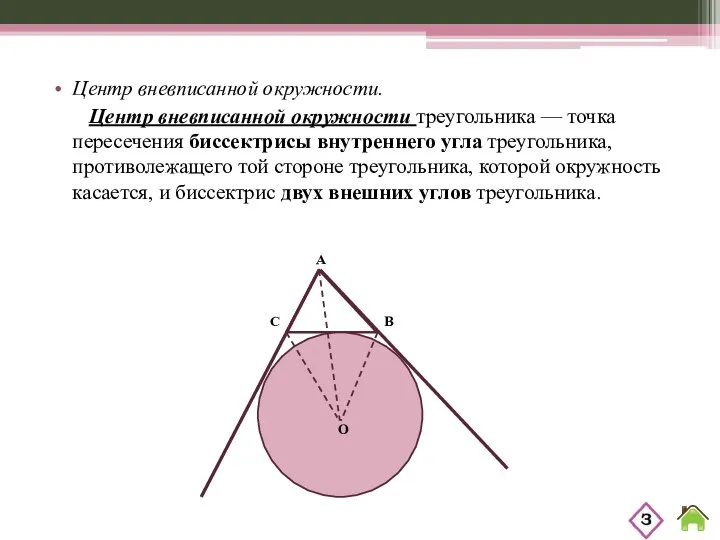
- 5. Центр вневписанной окружности. Центр вневписанной окружности треугольника — точка пересечения биссектрисы внутреннего угла треугольника, противолежащего той
- 6. Дано: ΔABC; Вневписанная окр. (Оа;rа) Доказать: Док-во: Т.к. касательные, проведенные из одной точки, равны ,то ВВ1=ВА1,
- 7. Дано: ΔABC; Вневписанная окр. (Оа;rа) Доказать: Док-во: В прямоугольном треугольнике ΔАОаС1 ra и – длины катетов,
- 8. III. Радиус вневписанной окружности, касающейся данной стороны треугольника, равен отношению площади треугольника к разности полупериметра и
- 9. Задачи на свойства касательной к вневписанной окружности и ее радиусов:
- 10. Задача№1. Найдите периметр треугольника АВС, если расстояние от вершины А до точки касания с вневписанной окружностью
- 11. Решение №2: 1) Т.к АВ1 = АС1 = ( по теореме о касательной вневписанной окружности), то
- 12. Задача№2. РЕШЕНИЕ Задача№2. Найдите радиус вневписанной окружности треугольника со сторонами 13, 13, 10. (ЕГЭ-2015, система задач
- 13. Решение 1: Дано: Окр(Оа;rа);ΔАВС;AB=13, AC=13, BC=10. Найти: rа -?. Решение (1 случай) : 1. Пусть стороны
- 14. Решение 2: Дано: Окр(Оc;rc);ΔАВС;AB=13, AC=13, BC=10. Найти: rc -?. Решение (2 случай): 1. Пусть Oc —
- 15. Задача№3. Найдите радиус вневписанной окружности, если расстояние от вершины А до точки касания с окружностью равно
- 16. Дано: AB1=21, AB=14, AC=13, BC=15. Найти: ra-?. Решение : 1) Рассмотрим ΔABC : 2) 3) По
- 17. 2. Соотношения с радиусами вневписанных окружностей.
- 18. Выражение суммы радиусов вневписанных окружностей через радиус вписанной окружности и радиус описанной окружности. Дано: ΔABC; Вневписанная
- 19. Выражение суммы величин, обратных радиусам вневписанных окружностей, через величину обратную радиусу вписанных окружностей. Выражение суммы всех
- 20. Выражение произведения радиусов вневписанных окружностей через произведение радиуса вписанной окружности и квадрат полупериметра треугольника. Дано: ΔABC;
- 21. 1 следствие: Площадь треугольника равна отношению произведения всех трех радиусов вневписанных окружностей к полупериметру треугольника. Дано:
- 22. 2 следствие: Площадь треугольника равна квадратному корню из произведения всех трех радиусов вневписанных окружностей и радиуса
- 23. Задачи на соотношения с радиусов вневписанных окружностей:
- 24. Задачи: Задача№4. Найдите радиус вневписанной окружности треугольника, если радиусы двух других вневписанных окружностей равны 2002 и
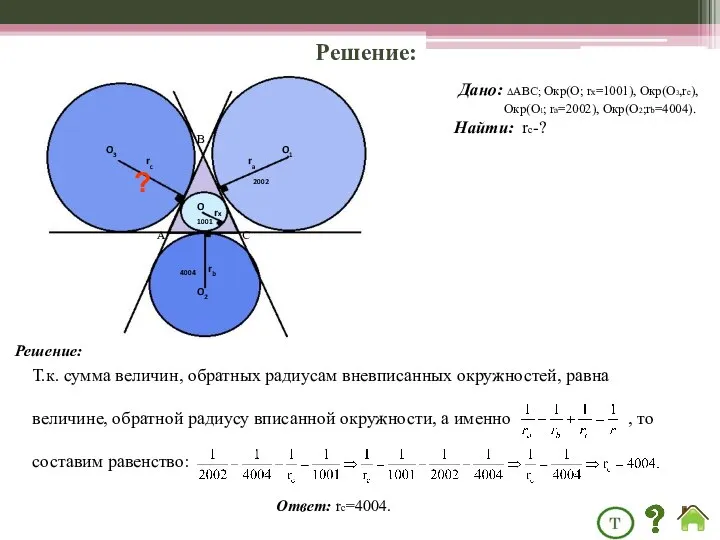
- 25. Решение: Дано: ΔABC; Окр(О; rх=1001), Окр(О3,rс), Окр(О1; rа=2002), Окр(О2;rb=4004). Найти: rс-? Т.к. сумма величин, обратных радиусам
- 26. Задачи: Задача №5. Найдите произведение сторон треугольника, если известно, что радиусы его вневписанных окружностей равны 9,18
- 27. Решение: Дано: ΔABC; ra=9, rb=18, rc=21;Окр(О, rс), Окр(О; rа), Окр(О; rb), Окр(О; R). Найти: , следовательно
- 28. Задачи: Задача №6. Найдите произведение радиусов всех вневписанных окружностей треугольника со сторонами 4,5,6. (сборник «Подготовка к
- 29. Решение: Дано: ΔABC; a=4, b=5, c=6;Окр(О, rс), Окр(О; rа), Окр(О; rb) Найти: 2. Так как ,
- 30. Задачи: Задача№7. Основание АС равнобедренного треугольника равно 10. Окружность радиуса 7,5 с центром вне этого треугольника
- 31. 3. АК – высота, проведенная к гипотенузе => AK²=FK*KO ( по теореме о высоте прямоугольного Δ)
- 33. Скачать презентацию




























 Применение средств ЭВМ при обработке данных активного эксперимента
Применение средств ЭВМ при обработке данных активного эксперимента Свойства определенного интеграла
Свойства определенного интеграла Построение диаграмм и графиков
Построение диаграмм и графиков Урок математики 2 класс Шаршукова В.А., учитель начальных классов МАОУСОШ № 8 г.Старая Русса
Урок математики 2 класс Шаршукова В.А., учитель начальных классов МАОУСОШ № 8 г.Старая Русса Умножение обыкновенных дробей. 6 класс
Умножение обыкновенных дробей. 6 класс Проверка статистических гипотез (лекция 8)
Проверка статистических гипотез (лекция 8) Симметрия в окружающем мире. Симметрия в человеческом творчестве. Орнаменты
Симметрия в окружающем мире. Симметрия в человеческом творчестве. Орнаменты Урок - морское путешествие. Дробные выражения
Урок - морское путешествие. Дробные выражения Путешествие в сказку математика
Путешествие в сказку математика Различие треугольников по длинам сторон и по видам углов
Различие треугольников по длинам сторон и по видам углов Линейность изображений
Линейность изображений ПРОБЛЕМЫ СИСТЕМАТИЧЕСКИХ И СЛУЧАЙНЫХ ОШИБОК
ПРОБЛЕМЫ СИСТЕМАТИЧЕСКИХ И СЛУЧАЙНЫХ ОШИБОК  Презентация по математике "Системы исчисления" - скачать бесплатно
Презентация по математике "Системы исчисления" - скачать бесплатно Презентация по математике "Тригонометрические функции числового аргумента" - скачать
Презентация по математике "Тригонометрические функции числового аргумента" - скачать  «Преобразование целого выражения в многочлен» Подготовила учитель математики Гомонова Галина Васильевна
«Преобразование целого выражения в многочлен» Подготовила учитель математики Гомонова Галина Васильевна Квадратные уравнения. 8 класс
Квадратные уравнения. 8 класс Игры Мудрой Совы
Игры Мудрой Совы Статистическая обработка вариационного ряда
Статистическая обработка вариационного ряда Центральные и вписанные углы
Центральные и вписанные углы Числовая окружность
Числовая окружность Метрические пространства
Метрические пространства Круг и отрезок
Круг и отрезок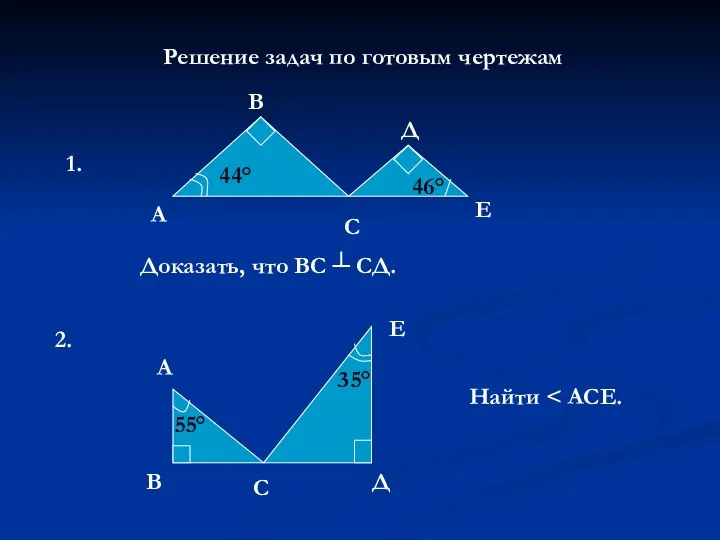 Прямоугольные треугольники. Решение задач по готовым чертежам
Прямоугольные треугольники. Решение задач по готовым чертежам Задачи на построение треугольника. Урок геометрии в 7 классе
Задачи на построение треугольника. Урок геометрии в 7 классе Вимірювальні прибори
Вимірювальні прибори Система однородных линейных уравнений
Система однородных линейных уравнений Тренажёр. Таблица умножения. «Юные водители»
Тренажёр. Таблица умножения. «Юные водители» Обернена тригонометрична функція y=arcsinx
Обернена тригонометрична функція y=arcsinx