Вневписанная окружность Геометрия является самым могущественным средством для изощрения наших умственных способностей и дает

Август 25, 2022

Главная
Математика
Вневписанная окружность Геометрия является самым могущественным средством для изощрения наших умственных способностей и дает

Содержание

2. Вневписанная окружность Простейший из многоугольников — треугольник — играет в геометрии особую роль. За несколько тысячелетий
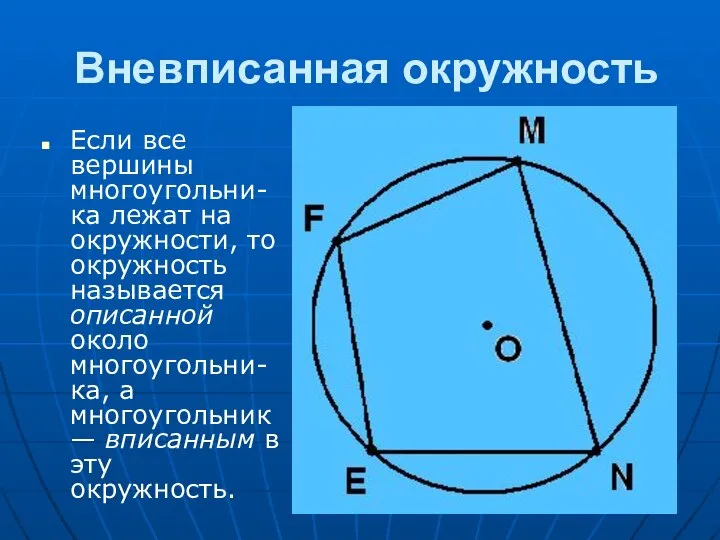
3. Вневписанная окружность Если все вершины многоугольни-ка лежат на окружности, то окружность называется описанной около многоугольни-ка, а
4. Вневписанная окружность Если все стороны многоугольника касаются окружности, то окружность называется вписанной в многоугольник, а многоугольник
5. Вневписанная окружность Три серединных перпендикуля-ра к сторонам треугольника пересекаются в одной точке — центре описанной около
6. Вневписанная окружность Биссектрисы внутренних углов треугольника пересекаются в одной точке- центре вневписанной в этот треугольник окружности.
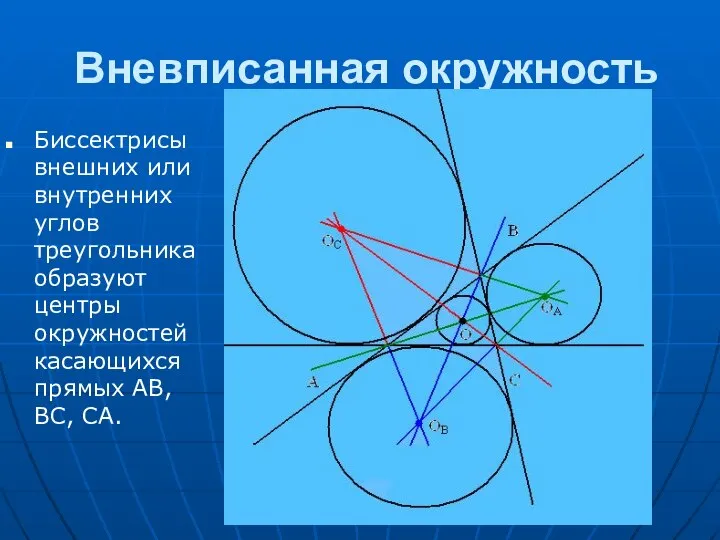
7. Вневписанная окружность Биссектрисы внешних или внутренних углов треугольника образуют центры окружностей касающихся прямых АВ, ВС, СА.
8. Вневписанная окружность В итоге получаем четыре окружности с центрами О, Оа, Ob, Oc, касающиеся трех данных
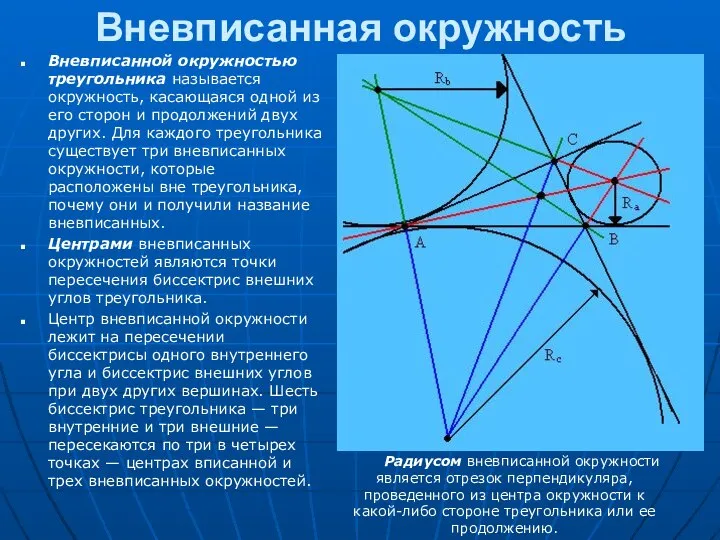
9. Вневписанная окружность Вневписанной окружностью треугольника называется окружность, касающаяся одной из его сторон и продолжений двух других.
10. Вневписанная окружность Свойство вневписанной окружности и ее связь с основными элементами треугольника Теорема. Пусть К1 —
11. Вневписанная окружность Доказательство: 1). Пусть точки К2 и К3 — точки касания вневписанной окружности с прямыми
12. Вневписанная окружность Интересно, что отрезки, соединяющие центр вписанной в треугольник окружности с центрами вневписанных окружностей, делятся
14. Скачать презентацию

Слайд 2

Вневписанная окружность
Простейший из многоугольников — треугольник — играет в геометрии особую

роль. За несколько тысячелетий геометры столь подробно изучили треугольник, что иногда говорят о «геометрии треугольника» как о самостоятельном разделе элементарной геометрии.
Первые упоминания о треугольнике и его свойствах можно найти в египетских папирусах, которым более 4000 лет. Через 2000 лет в Древней Греции изучение свойств треугольника достигает высокого уровня — достаточно вспомнить теорему Пифагора и формулу Герона.
Центральное место в геометрии треугольника занимают свойства так называемых замечательных точек и линий.

Слайд 3

Вневписанная окружность
Если все вершины многоугольни-ка лежат на окружности, то окружность называется

описанной около многоугольни-ка, а многоугольник — вписанным в эту окружность.

Слайд 4

Вневписанная окружность

Если все стороны многоугольника касаются окружности, то окружность называется

вписанной в многоугольник, а многоугольник — описанным около этой окружности.

Слайд 5

Вневписанная окружность
Три серединных перпендикуля-ра к сторонам треугольника пересекаются в одной точке

— центре описанной около треугольника окружности.

Слайд 6

Вневписанная окружность
Биссектрисы внутренних углов треугольника пересекаются в одной точке- центре вневписанной

в этот треугольник окружности.

Если рассмотреть дополнительно биссектрисы трех пар внешних углов треугольника, то получаются еще три замечательных точки — центры вневписанных окружностей.

Слайд 7

Вневписанная окружность
Биссектрисы внешних или внутренних углов треугольника образуют центры окружностей касающихся

прямых АВ, ВС, СА.

Слайд 8

Вневписанная окружность
В итоге получаем четыре окружности с центрами О, Оа, Ob,

Oc, касающиеся трех данных несовпадающих прямых. При этом одна из них будет вписанной в треугольник окружностью, а три других — вневписанными окружностями.

Слайд 9

Вневписанная окружность
Вневписанной окружностью треугольника называется окружность, касающаяся одной из его сторон

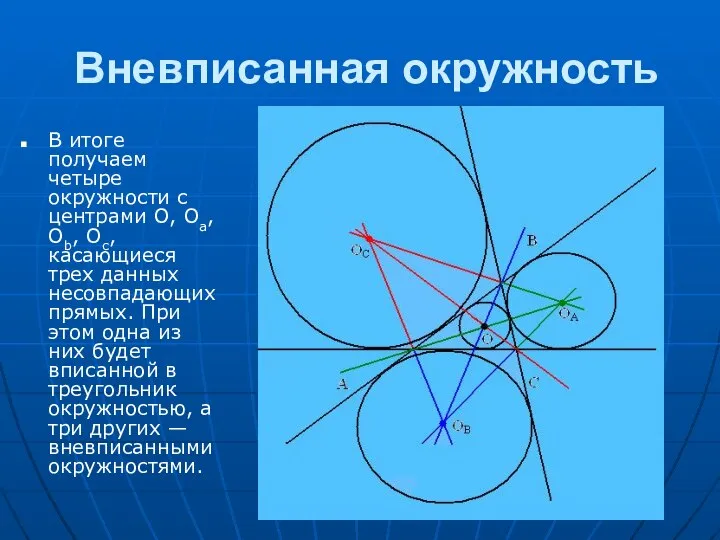
и продолжений двух других. Для каждого треугольника существует три вневписанных окружности, которые расположены вне треугольника, почему они и получили название вневписанных.
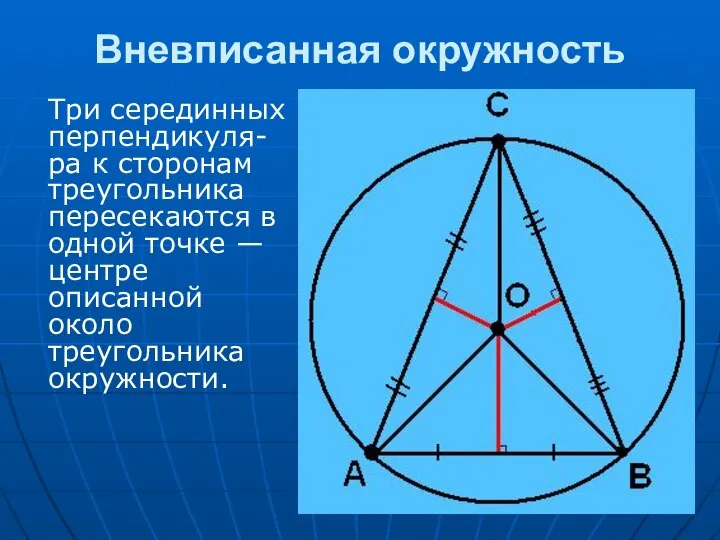
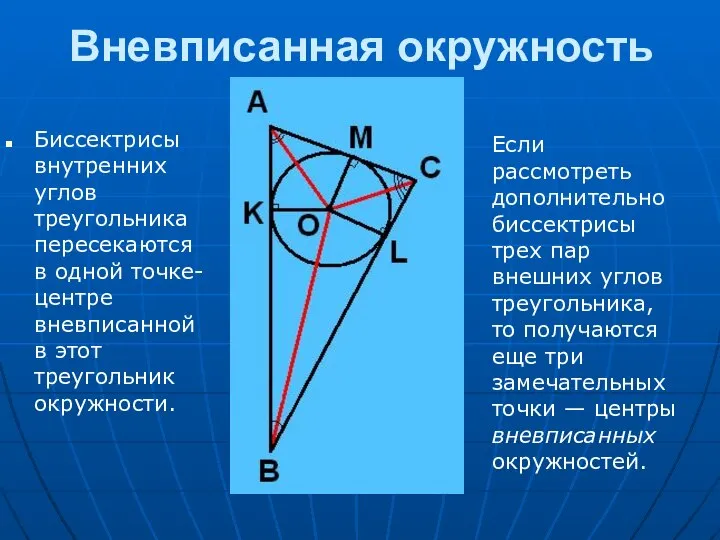
Центрами вневписанных окружностей являются точки пересечения биссектрис внешних углов треугольника.
Центр вневписанной окружности лежит на пересечении биссектрисы одного внутреннего угла и биссектрис внешних углов при двух других вершинах. Шесть биссектрис треугольника — три внутренние и три внешние — пересекаются по три в четырех точках — центрах вписанной и трех вневписанных окружностей.

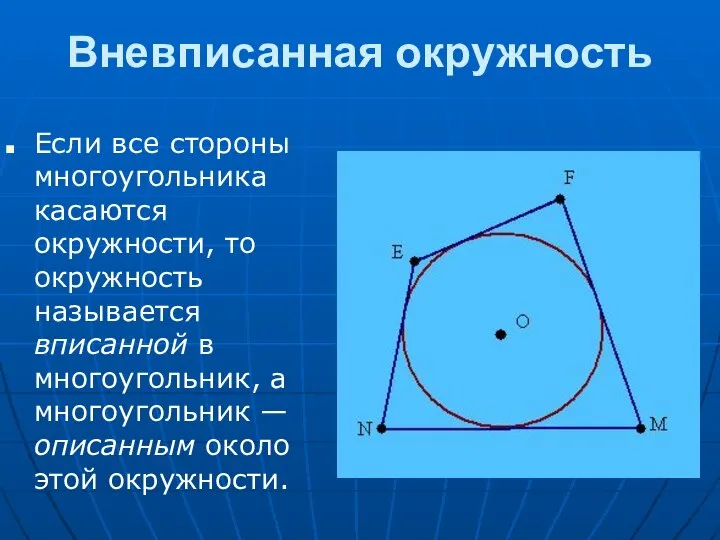
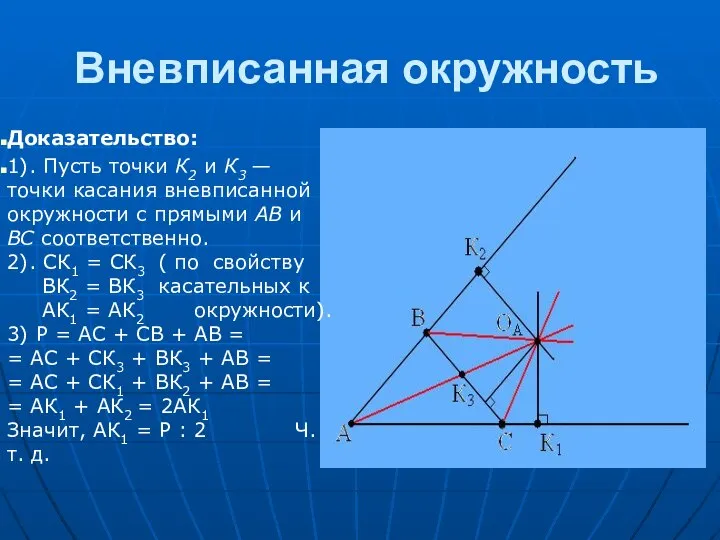
Радиусом вневписанной окружности является отрезок перпендикуляра, проведенного из центра окружности к какой-либо стороне треугольника или ее продолжению.

Слайд 10

Вневписанная окружность
Свойство вневписанной окружности и ее связь с основными элементами треугольника
Теорема.

Пусть К1 — точка касания вневписанной окружности с продолжением стороны АС треугольника ABC. Тогда длина отрезка АК1 равна полупериметру треугольника ABC.

Слайд 11

Вневписанная окружность
Доказательство:
1). Пусть точки К2 и К3 — точки касания

вневписанной окружности с прямыми АВ и ВС соответственно.
2). СК1 = СК3 ( по свойству
ВК2 = ВК3 касательных к
АК1 = АК2 окружности).
3) Р = АС + СВ + АВ =
= АС + СК3 + ВК3 + АВ =
= АС + СК1 + ВК2 + АВ =
= АК1 + АК2 = 2АК1
Значит, АК1 = Р : 2 Ч. т. д.

Слайд 12

Вневписанная окружность
Интересно, что отрезки, соединяющие центр вписанной в треугольник окружности с

центрами вневписанных окружностей, делятся пополам окружностью, описанной вокруг этого треугольника

Вневписанная окружность Геометрия является самым могущественным средством для изощрения наших умственных способностей и дает

Содержание

Вневписанная окружностьПростейший из многоугольников — треугольник — играет в геометрии особую

Вневписанная окружностьЕсли все вершины многоугольни-ка лежат на окружности, то окружность называется

Вневписанная окружность Если все стороны многоугольника касаются окружности, то окружность называется

Вневписанная окружность Три серединных перпендикуля-ра к сторонам треугольника пересекаются в одной точке

Вневписанная окружностьБиссектрисы внутренних углов треугольника пересекаются в одной точке- центре вневписанной

Вневписанная окружностьБиссектрисы внешних или внутренних углов треугольника образуют центры окружностей касающихся

Вневписанная окружностьВ итоге получаем четыре окружности с центрами О, Оа, Ob,

Вневписанная окружностьВневписанной окружностью треугольника называется окружность, касающаяся одной из его сторон

Вневписанная окружностьСвойство вневписанной окружности и ее связь с основными элементами треугольникаТеорема.

Вневписанная окружностьДоказательство: 1). Пусть точки К2 и К3 — точки касания

Вневписанная окружностьИнтересно, что отрезки, соединяющие центр вписанной в треугольник окружности с

Похожие презентации