Содержание
- 2. Воспользуемся формулой где m – любое действительное число. В нашем случае: бинома Ньютона:
- 4. Видно, что с ростом n увеличивается число положительных слагаемых, которых всего будет n+1, и растет величина
- 5. Теперь каждую дробь в правой части заменяем большей дробью с двойкой в знаменателе: Получаем:
- 6. Сумма есть сумма n-1 членов геометрической прогрессии, где первый член и знаменатель По формуле суммы членов
- 7. Т.к. Sn-1 Действительно, данная последовательность является ограниченной.
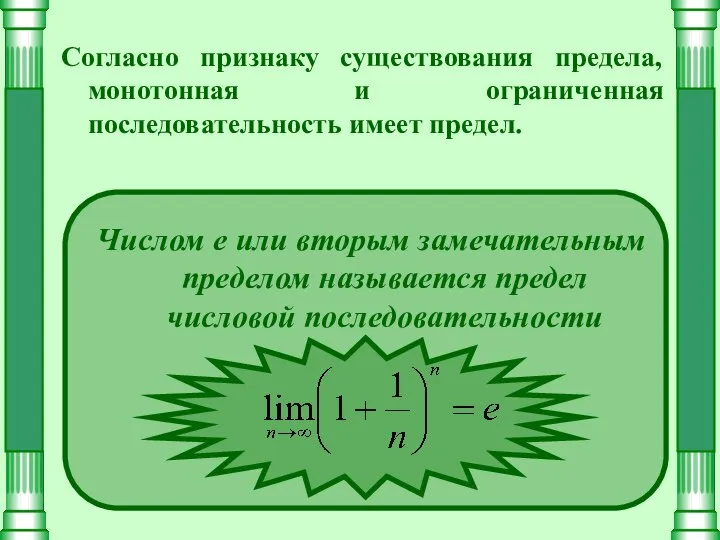
- 8. Согласно признаку существования предела, монотонная и ограниченная последовательность имеет предел. Числом е или вторым замечательным пределом
- 9. е – число Эйлера е=2,718281… Можно показать, что функция при где х пробегает все значения, а
- 10. Второй замечательный предел
- 11. Пусть , тогда Второй замечательный предел
- 12. Примеры. 1 Вычислить
- 13. Решение:
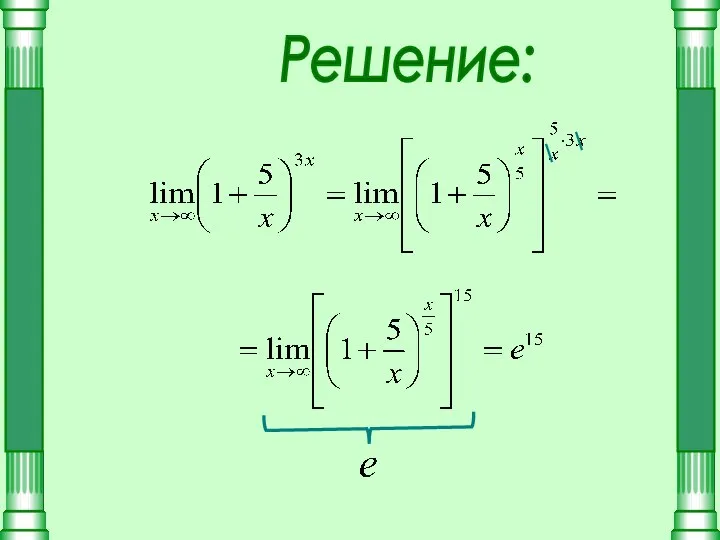
- 14. 2 Вычислить
- 15. Решение:
- 16. 3 В качестве еще одного примера рассмотрим задачу о непрерывном начислении процентов. Первоначальный вклад в банк
- 17. То есть На практике часто применяются сложные проценты. В этом случае размер вклада ежегодно будет увеличиваться
- 18. Если начислять проценты не один, а n раз в году, то при ежегодном приросте Р %,
- 19. Будем полагать, что проценты по вкладу начисляются каждое полугодие (n=2), ежеквартально (n=4), ежемесячно (n=12), каждый день
- 21. Скачать презентацию

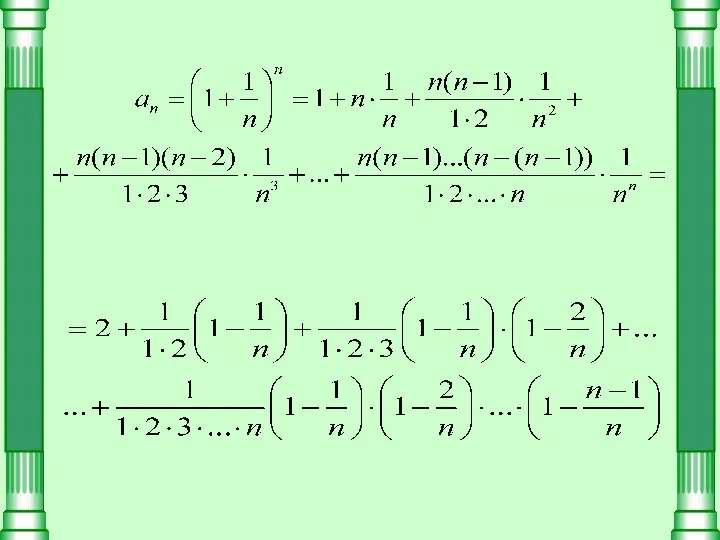














 Свойства степени с целым показателем
Свойства степени с целым показателем Бихроматические графы
Бихроматические графы Степень числа. Квадрат и куб числа. 5 класс
Степень числа. Квадрат и куб числа. 5 класс Сокращение дробей
Сокращение дробей Многоугольники, описанные около окружности
Многоугольники, описанные около окружности Локальные степени вершин графа
Локальные степени вершин графа Презентация по математике "Математические развлечения" - скачать
Презентация по математике "Математические развлечения" - скачать  Тема урока: «Закрепление умений сложения и вычитания в пределах .» Класс, для которого разработан урок или рекомендуемый возрас
Тема урока: «Закрепление умений сложения и вычитания в пределах .» Класс, для которого разработан урок или рекомендуемый возрас Решение систем линейных неравенств с одной переменной (9 класс)
Решение систем линейных неравенств с одной переменной (9 класс) Пак Наталья Николаевна Пак Наталья Николаевна Учитель математики ГБОУ лицей 179 Урок геометрии в 8 классе
Пак Наталья Николаевна Пак Наталья Николаевна Учитель математики ГБОУ лицей 179 Урок геометрии в 8 классе  Тела вращения
Тела вращения Дискретные случайные величины
Дискретные случайные величины Область определения функции
Область определения функции Презентация на тему Все профессии с математикой дружны
Презентация на тему Все профессии с математикой дружны  Упрощение выражений (5 класс)
Упрощение выражений (5 класс) Деление десятичной дроби на десятичную дробь
Деление десятичной дроби на десятичную дробь Математические модели. Текстовые задачи по математике
Математические модели. Текстовые задачи по математике Комплексные числа
Комплексные числа Каркасы графа. (Лекция 6)
Каркасы графа. (Лекция 6) Математика для малышей Один много
Математика для малышей Один много Здоровьесберегающие технологии на уроках математики
Здоровьесберегающие технологии на уроках математики Радианная мера угла
Радианная мера угла Презентация по математике "Решение задач" - скачать бесплатно
Презентация по математике "Решение задач" - скачать бесплатно Пропорции
Пропорции Решение уравнения. (Задание 13)
Решение уравнения. (Задание 13) Задачи на движение. Часть 2
Задачи на движение. Часть 2 Презентация по математике "Множество. Операции над множествами" - скачать бесплатно
Презентация по математике "Множество. Операции над множествами" - скачать бесплатно Лозунговый шифр
Лозунговый шифр