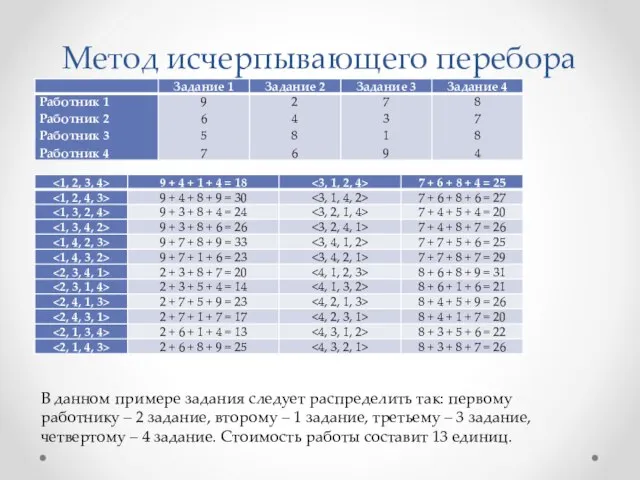
Задачей является распределение всех подлежащих назначению единиц в клетки с нулевой
стоимостью.
Этап 2. Выбираем строку с одним нулем (строка №1), выделяем нуль жирным и зачеркиваем (выделено серым) оставшиеся нулевые значения этого столбца (столбца №3).
Выбираем строку с одним нулевым значением (строка №5), выделяем нуль.
Выбираем строку с одним нулем (строка №3), выделяем нуль жирным и зачеркиваем (выделено серым) оставшиеся нулевые значения этого столбца (столбца №4).
Выбираем строку с одним нулем (строка №4), выделяем нуль жирным и зачеркиваем (выделено серым) оставшиеся нулевые значения этого столбца (столбца №1). Выбираем строку с одним нулевым значением (строка №2), выделяем нуль.
Получаем оптимальную матрицу назначений:
Минимальное значение целевой функции: 1+2+2+1+2=8.






 Матрицы и действия над ними
Матрицы и действия над ними Статистические методы обработки медико-биологических данных. Нормальный закон распределения
Статистические методы обработки медико-биологических данных. Нормальный закон распределения Упрощение выражений
Упрощение выражений Цилиндр. Цилиндрическая поверхность. Площадь полной поверхности и объем цилиндра
Цилиндр. Цилиндрическая поверхность. Площадь полной поверхности и объем цилиндра Кривые второго порядка на плоскости
Кривые второго порядка на плоскости Архитектура и геометрия
Архитектура и геометрия Развитие творческой деятельности учащихся в процессе составления задач по историческим данным краеведческого характера
Развитие творческой деятельности учащихся в процессе составления задач по историческим данным краеведческого характера Площадь параллелограмма, треугольника и трапеции. Урок 18
Площадь параллелограмма, треугольника и трапеции. Урок 18 Параллелограмм. Свойства. Признаки
Параллелограмм. Свойства. Признаки Осевая и центральная симметрия
Осевая и центральная симметрия Математика в реальной жизни
Математика в реальной жизни Цилиндр. Правильный круглый цилиндр. Эллиптический цилиндр
Цилиндр. Правильный круглый цилиндр. Эллиптический цилиндр Площадь треугольника
Площадь треугольника Симметрия. Виды симметрии
Симметрия. Виды симметрии Перпендикулярность прямой и плоскости
Перпендикулярность прямой и плоскости Счёт предметов. Цифра 5
Счёт предметов. Цифра 5 Методы численного дифференцирования. Алгоритмы методов Эйлера
Методы численного дифференцирования. Алгоритмы методов Эйлера Презентация на тему Немного о дробях
Презентация на тему Немного о дробях  Метапредметные результаты. Компетентностноориентированные задания. 9 класс
Метапредметные результаты. Компетентностноориентированные задания. 9 класс Одночлен и его стандартный вид. 7 класс
Одночлен и его стандартный вид. 7 класс Статистические исследования
Статистические исследования Выделение целой части из неправильной дроби
Выделение целой части из неправильной дроби Деление рациональных дробей (Урок алгебры 8 класс)
Деление рациональных дробей (Урок алгебры 8 класс) Functions of Random Variables 2. Method of Distribution Functions
Functions of Random Variables 2. Method of Distribution Functions Презентация "Математики"
Презентация "Математики" Учитель: Зимина Марина Евгеньевна МОУ СОШ№8 г. Саранск Урок-путешествие к острову Натуральных чисел
Учитель: Зимина Марина Евгеньевна МОУ СОШ№8 г. Саранск Урок-путешествие к острову Натуральных чисел Подобие треугольников. Задачи
Подобие треугольников. Задачи Оформлення геометричних задач
Оформлення геометричних задач