Содержание
- 2. Copyright © Cengage Learning. All rights reserved. Functions Defined on General Sets SECTION 7.1
- 3. Functions Defined on General Sets We have already defined a function as a certain type of
- 4. Arrow Diagrams
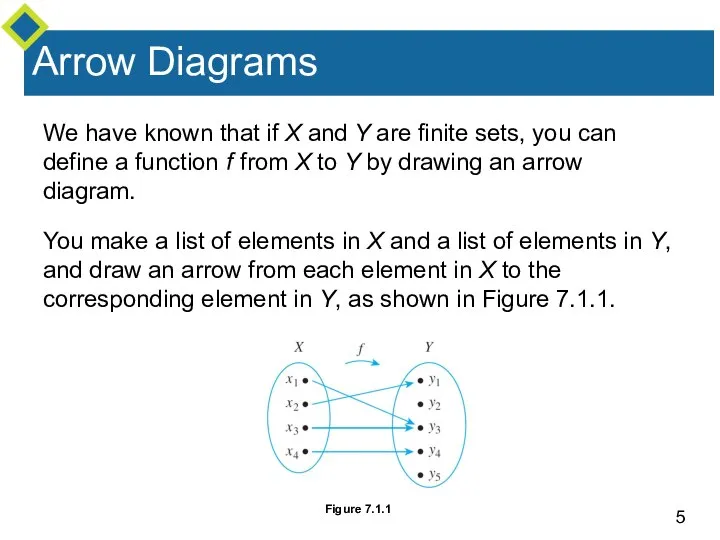
- 5. Arrow Diagrams We have known that if X and Y are finite sets, you can define
- 6. Arrow Diagrams This arrow diagram does define a function because 1. Every element of X has
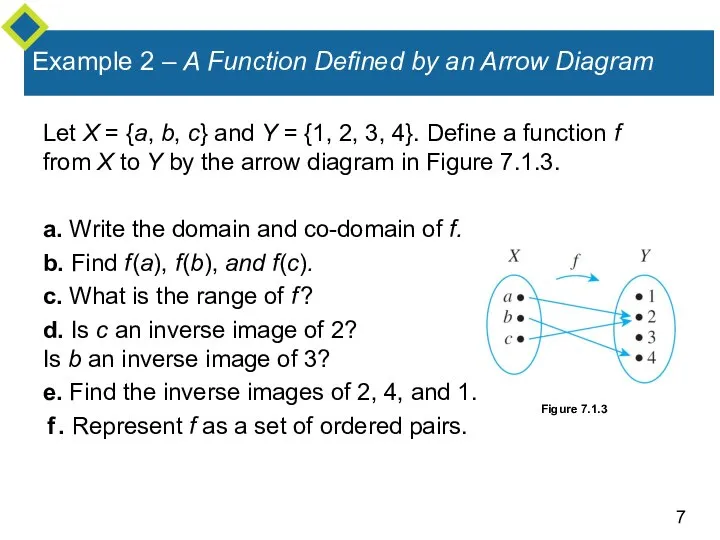
- 7. Example 2 – A Function Defined by an Arrow Diagram Let X = {a, b, c}
- 8. Example 2 – Solution a. domain of co-domain of b. c. range of d. Yes, No
- 9. Arrow Diagrams In Example 2 there are no arrows pointing to the 1 or the 3.
- 10. Arrow Diagrams Earlier we have given a test for determining whether two functions with the same
- 11. Example 3 – Equality of Functions a. Let J3 = {0, 1, 2}, and define functions
- 12. Example 3 – Solution a. Yes, the table of values shows that f (x) = g(x)
- 13. Examples of Functions
- 14. Example 4 – The Identity Function on a Set Given a set X, define a function
- 15. Example 4 – Solution Whatever is input to the identity function comes out unchanged, so and
- 16. Examples of Functions
- 17. Example 8 – The Logarithmic Function with Base b Find the following: a. b. c. d.
- 18. Example 8 – Solution d. because the exponent to which 2 must be raised to obtain
- 19. Examples of Functions We have known that if S is a nonempty, finite set of characters,
- 20. Example 9 – Encoding and Decoding Functions Digital messages consist of finite sequences of 0’s and
- 21. Example 9 – Encoding and Decoding Functions The receiver of the message decodes it by replacing
- 22. Example 9 – Encoding and Decoding Functions The encoding function E is the function from A
- 23. Example 9 – Encoding and Decoding Functions The advantage of this particular coding scheme is that
- 24. Boolean Functions
- 25. Boolean Functions We have discussed earlier that how to find input/output tables for certain digital logic
- 26. Boolean Functions
- 27. Example 11 – A Boolean Function Consider the three-place Boolean function defined from the set of
- 28. Example 11 – Solution The rest of the values of f can be calculated similarly to
- 29. Checking Whether a Function Is Well Defined
- 30. Checking Whether a Function Is Well Defined It can sometimes happen that what appears to be
- 31. Checking Whether a Function Is Well Defined For instance, when x = 2, there is no
- 32. Example 12 – A Function That Is Not Well Defined We know that Q represents the
- 33. Example 12 – Solution The function f is not well defined. The reason is that fractions
- 34. Example 12 – Solution But applying the formula for f, you find that and so This
- 35. Checking Whether a Function Is Well Defined Note that the phrase well-defined function is actually redundant;
- 36. Functions Acting on Sets
- 37. Functions Acting on Sets Given a function from a set X to a set Y, you
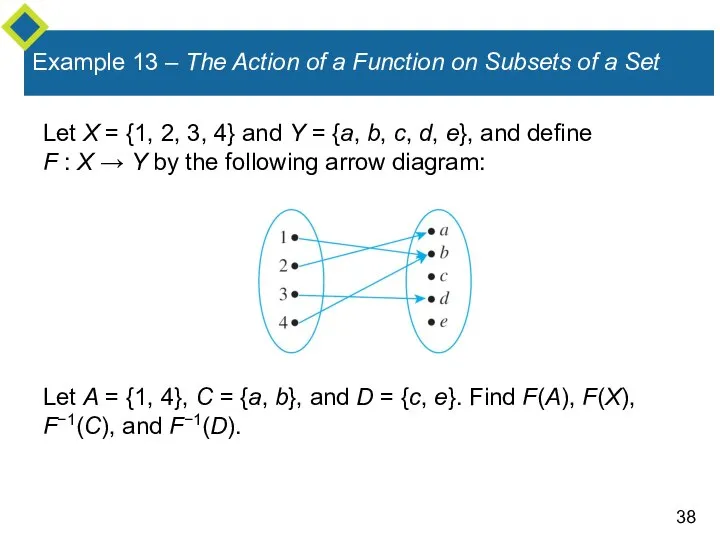
- 38. Example 13 – The Action of a Function on Subsets of a Set Let X =
- 40. Скачать презентацию


































 Szaty Liturgiczne
Szaty Liturgiczne Creation of the Kalevala Epic
Creation of the Kalevala Epic Контроллеры для систем автоматизации
Контроллеры для систем автоматизации Изуальный осмотр помещений, проводимый для выявления возможно внедрённых средств съёма информации
Изуальный осмотр помещений, проводимый для выявления возможно внедрённых средств съёма информации Советы по энергосбережению от фиксиков
Советы по энергосбережению от фиксиков Christmas Tree
Christmas Tree Станок рейсмусовый СР3-6А
Станок рейсмусовый СР3-6А Паспорт проекта: Фестиваль декоративно-прикладного творчества Новогоднее чудо
Паспорт проекта: Фестиваль декоративно-прикладного творчества Новогоднее чудо polina
polina Железобетонные фундаменты
Железобетонные фундаменты кл - алгоритм
кл - алгоритм 20130724_istoriya_konkurs
20130724_istoriya_konkurs Коды ошибок Павлова
Коды ошибок Павлова 20171119_moi_prava
20171119_moi_prava Проектирование технологического процесса изготовления детали зубчатое колесо в условиях массового типа производства
Проектирование технологического процесса изготовления детали зубчатое колесо в условиях массового типа производства Использование УЗВ для целей пресноводной и морской аквакультуры в Крыму
Использование УЗВ для целей пресноводной и морской аквакультуры в Крыму Технология плетения бисером и пайетками. Изготовление веточки вербы
Технология плетения бисером и пайетками. Изготовление веточки вербы стандарты общения
стандарты общения Емхана мен аурухананың әр түрлі бөлімдерінде емдеу- қорғау тәртібін жүргізу ерекшеліктері
Емхана мен аурухананың әр түрлі бөлімдерінде емдеу- қорғау тәртібін жүргізу ерекшеліктері Мій найкращий 4-Б
Мій найкращий 4-Б Проектирование системы электроснабжения коттеджа
Проектирование системы электроснабжения коттеджа Использование коряг, веток, коры деревьев в составлении композиций из природного материала
Использование коряг, веток, коры деревьев в составлении композиций из природного материала 20140530_svatko
20140530_svatko vrach
vrach Основы канализации
Основы канализации 3д моделирование из бумаги
3д моделирование из бумаги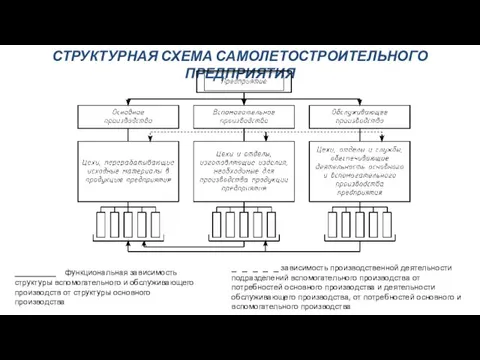 Структурная схема самолетостроительного предприятия
Структурная схема самолетостроительного предприятия Технология холодной сварки. (Лекция 14)
Технология холодной сварки. (Лекция 14)