Содержание
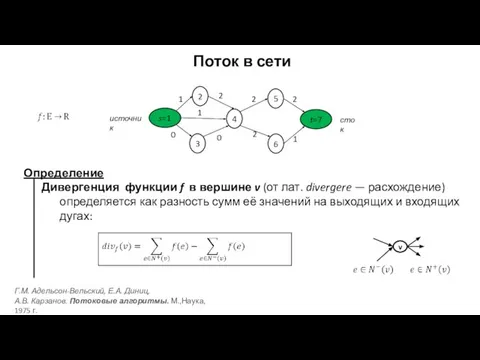
- 2. Поток в сети Определение Дивергенция функции f в вершине v (от лат. divergere — расхождение) определяется
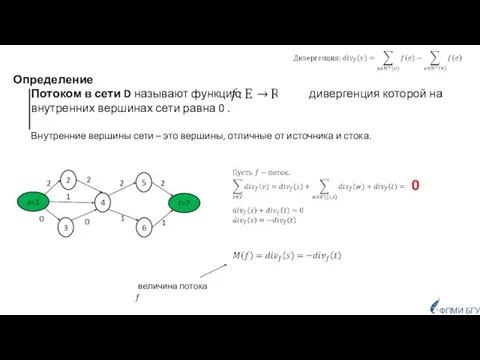
- 3. Определение Потоком в сети D называют функцию дивергенция которой на внутренних вершинах сети равна 0 .
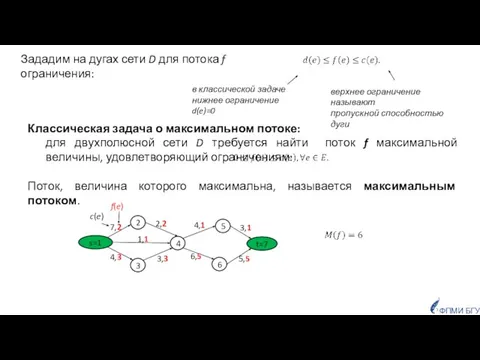
- 4. Зададим на дугах сети D для потока f ограничения: верхнее ограничение называют пропускной способностью дуги в
- 5. Замечания В дальнейшем мы будем работать с целочисленными потоками, то есть все ограничения – целые числа.
- 6. Максимальный поток и минимальный разрез X ФПМИ БГУ c f
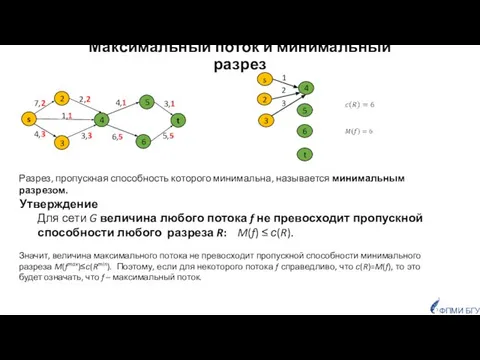
- 7. Максимальный поток и минимальный разрез Разрез, пропускная способность которого минимальна, называется минимальным разрезом. Утверждение Для сети
- 8. Лестер Рэндольф Форд младший англ. Lester Randolph Ford, Jr. 1927 – 2017 США Научная сфера -
- 9. Лестер Рэндольф Форд младший Метод Форда-Фалкерсона Делберт Рей Фалкерсон ФПМИ БГУ
- 10. Пусть f некоторый поток в сети D, тогда следующие утверждения эквивалентны: f – максимальный поток; для
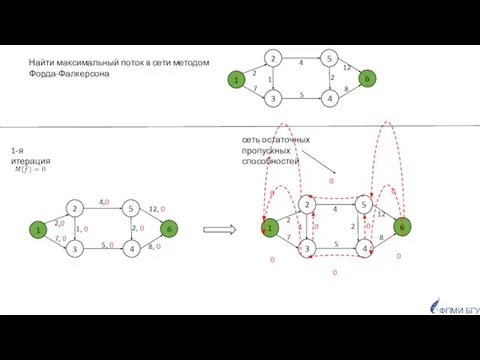
- 11. сеть остаточных пропускных способностей ФПМИ БГУ Найти максимальный поток в сети методом Форда-Фалкерсона 1-я итерация
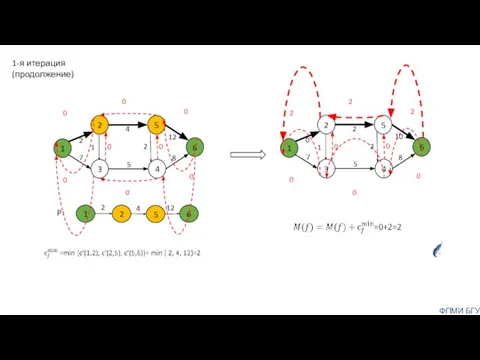
- 12. 1-я итерация (продолжение) ФПМИ БГУ
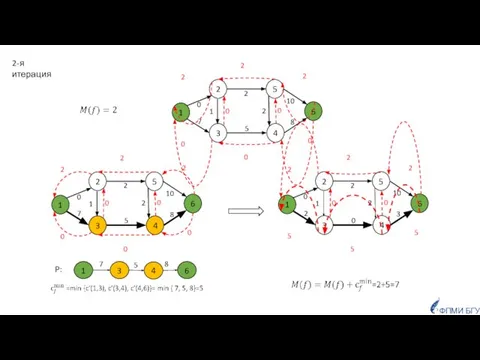
- 13. 2-я итерация ФПМИ БГУ
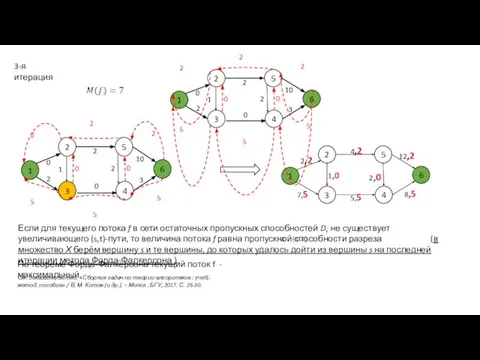
- 14. 3-я итерация См. доказательство: «Сборник задач по теории алгоритмов : учеб.-метод. пособие» / В. М. Котов
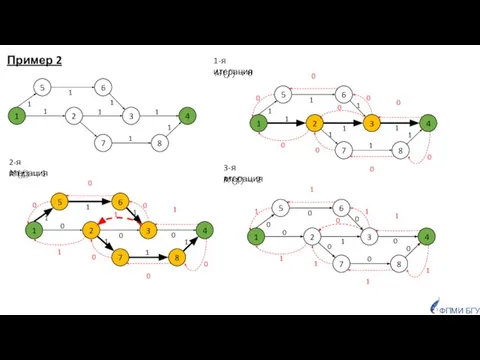
- 15. 1-я итерация 2-я итерация 3-я итерация ФПМИ БГУ Пример 2
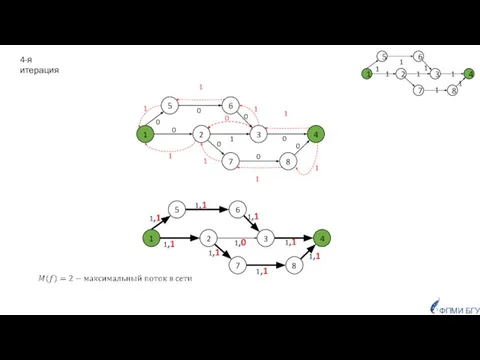
- 16. 4-я итерация ФПМИ БГУ
- 17. ФПМИ БГУ Метод Форда ̶ Фалкерсона Поэтому, если на итерациях метода Форда-Фалкерсона используется поиск в глубину,
- 18. ФПМИ БГУ Алгоритми Эдмондса ̶ Карпа полиномиальный алгоритм O(n+m) – время работы поиска в ширину; O(n·m)
- 19. работает для сетей с целочисленными пропускными способностями дуг O(сmax·n ·m) O(n · m2) ФПМИ БГУ Метод
- 20. 1: [ (2,2) , (5,3) ] cuv u v g 2: [ (9,3) , (3,4) ]
- 21. https://github.com/larandaA/alg-ds-snippets Псевдокод функций для работы с сетью остаточных пропускных способностей
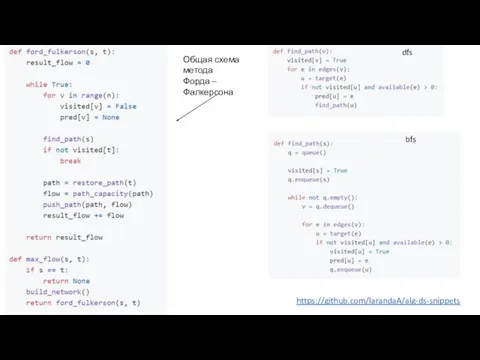
- 22. https://github.com/larandaA/alg-ds-snippets dfs bfs Общая схема метода Форда – Фалкерсона
- 23. Приложения ФПМИ БГУ
- 24. Наибольшее число попарно различных путей ФПМИ БГУ
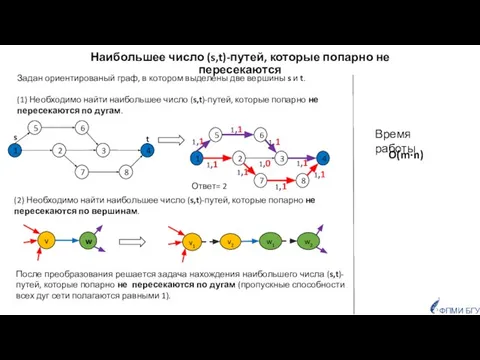
- 25. Наибольшее число (s,t)-путей, которые попарно не пересекаются Ответ= 2 Задан ориентированый граф, в котором выделены две
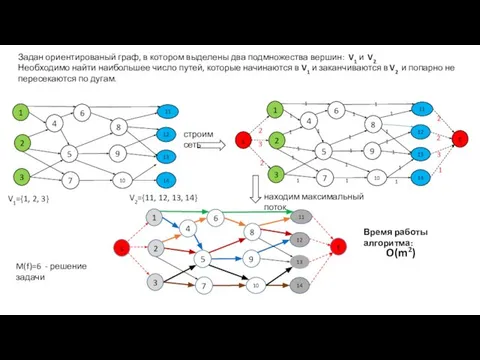
- 26. 2 3 1 2 3 2 2 M(f)=6 - решение задачи V1={1, 2, 3} V2={11, 12,
- 27. Наибольшее паросочетание в двудольном графе (англ. maximum matching) ФПМИ БГУ
- 28. Задан двудольный граф. Необходимо найти: наибольшее паросочетание; наибольшее паросочетание минимального веса (взвешенный граф). 1 2 4
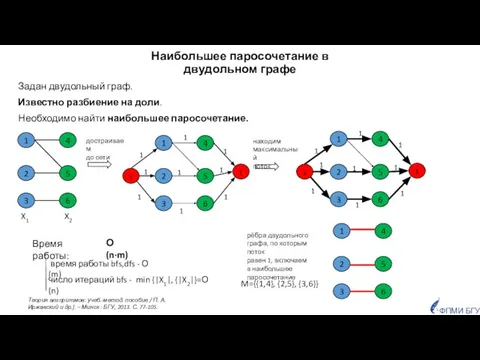
- 29. Наибольшее паросочетание в двудольном графе Задан двудольный граф. Известно разбиение на доли. Необходимо найти наибольшее паросочетание.
- 30. Наибольшее паросочетание минимального веса в двудольном графе ФПМИ БГУ
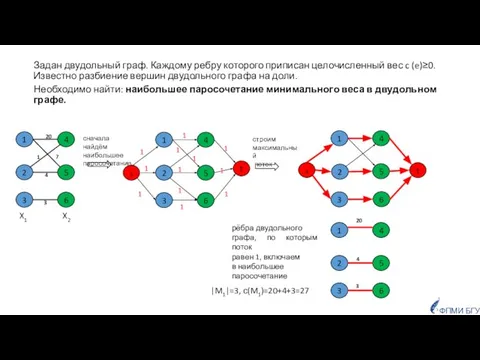
- 31. Задан двудольный граф. Каждому ребру которого приписан целочисленный вес c (e)≥0. Известно разбиение вершин двудольного графа
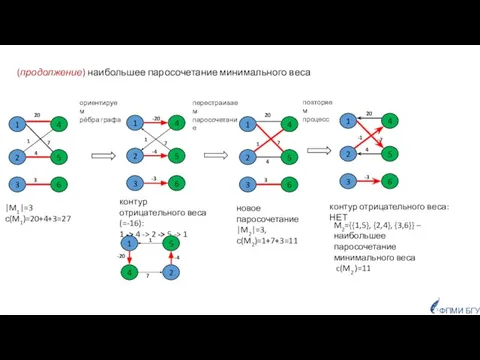
- 32. (продолжение) наибольшее паросочетание минимального веса контур отрицательного веса (=-16): 1 -> 4 -> 2 -> 5
- 33. ( O(n·m) + О(m)) Время работы алгоритма поиск наибольшего паросочетания в двудольном графе; О(cmax ·m ·
- 34. Максимальный поток минимальной стоимости (англ. max flow min cost) ФПМИ БГУ
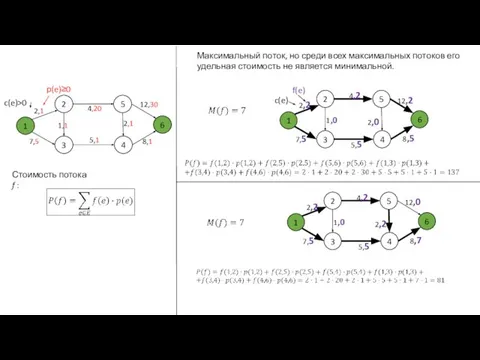
- 35. Стоимость потока f : Максимальный поток, но среди всех максимальных потоков его удельная стоимость не является
- 36. Максимальный поток минимальной стоимости Метод устранения отрицательных циклов ФПМИ БГУ
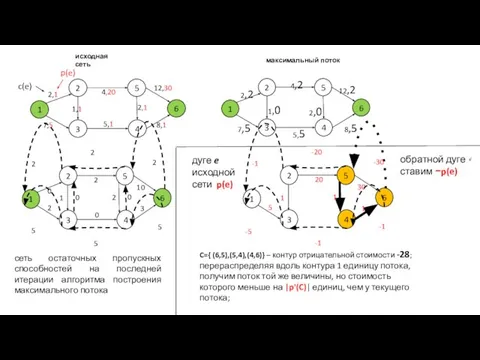
- 37. C={ (6,5),(5,4),(4,6)} – контур отрицательной стоимости -28; перераспределяя вдоль контура 1 единицу потока, получим поток той
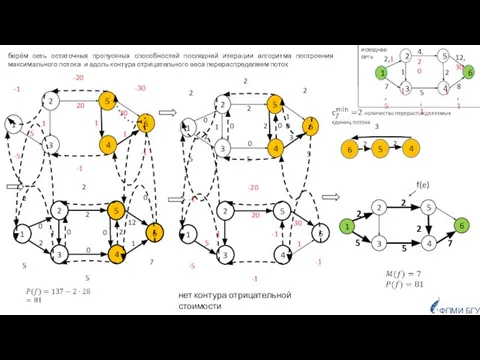
- 38. f(e) берём сеть остаточных пропускных способностей последней итерации алгоритма построения максимального потока и вдоль контура отрицательного
- 39. О(cmax · n · pmax) · Время работы: О(n·m2) – поиск максимального потока, например, алгоритмом Эдмондса
- 40. Максимальный поток минимальной стоимости Метод минимальных путей ФПМИ БГУ
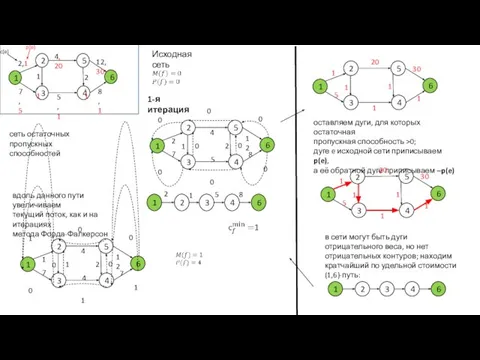
- 41. Исходная сеть сеть остаточных пропускных способностей 1-я итерация оставляем дуги, для которых остаточная пропускная способность >0;
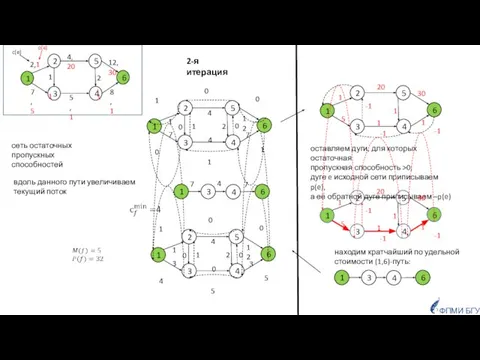
- 42. сеть остаточных пропускных способностей 2-я итерация оставляем дуги, для которых остаточная пропускная способность >0; дуге e
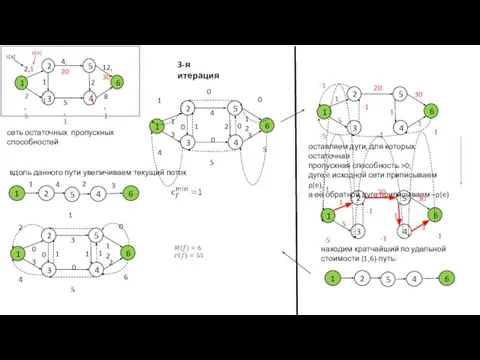
- 43. сеть остаточных пропускных способностей 3-я итерация оставляем дуги, для которых остаточная пропускная способность >0; дуге e
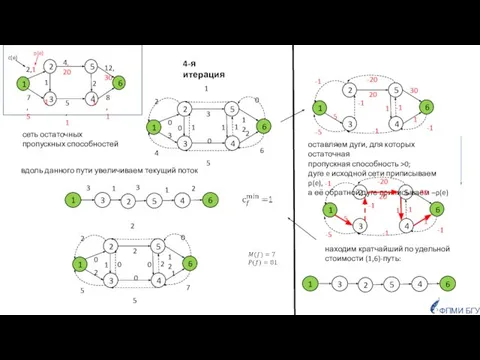
- 44. сеть остаточных пропускных способностей 4-я итерация оставляем дуги, для которых остаточная пропускная способность >0; дуге e
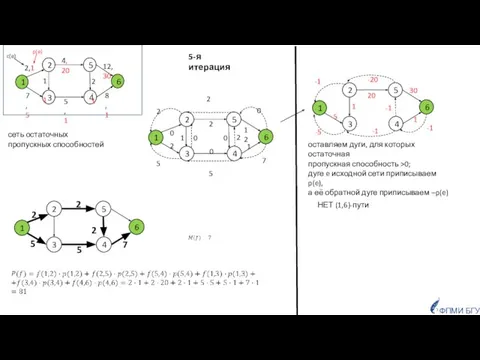
- 45. сеть остаточных пропускных способностей 5-я итерация оставляем дуги, для которых остаточная пропускная способность >0; дуге e
- 46. О(cmax · n) · (О(n·m) + О(m) ) Время работы О (cmax · m · n2)
- 47. Максимальный поток минимальной стоимости О(cmax · m · n2) Метод минимальных путей Метод устранения отрицательных циклов
- 48. Общие задачи в iRunner для закрепления навыков 0.11 Максимальный поток в сети (простая версия) 0.12 Максимальный
- 50. Скачать презентацию







![1: [ (2,2) , (5,3) ] cuv u v g 2:](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/557896/slide-19.jpg)














 Как величественны дела Твои, Господи, всё премудростью Ты сотворил
Как величественны дела Твои, Господи, всё премудростью Ты сотворил Пищевая и легкая промышленность
Пищевая и легкая промышленность Характерный портрет сказочного героя
Характерный портрет сказочного героя Обследование зданий и сооружений (продолжение)
Обследование зданий и сооружений (продолжение) Владимир Алексеевич Гиляровский
Владимир Алексеевич Гиляровский Электромагнитные колебания. Колебательный контур
Электромагнитные колебания. Колебательный контур Транзистор
Транзистор Остров Иммануаила Канта в г. Калининград
Остров Иммануаила Канта в г. Калининград Формирование выводов молекулярно-генетической экспертизы
Формирование выводов молекулярно-генетической экспертизы 20131020_povtorenie_dat_7_klass
20131020_povtorenie_dat_7_klass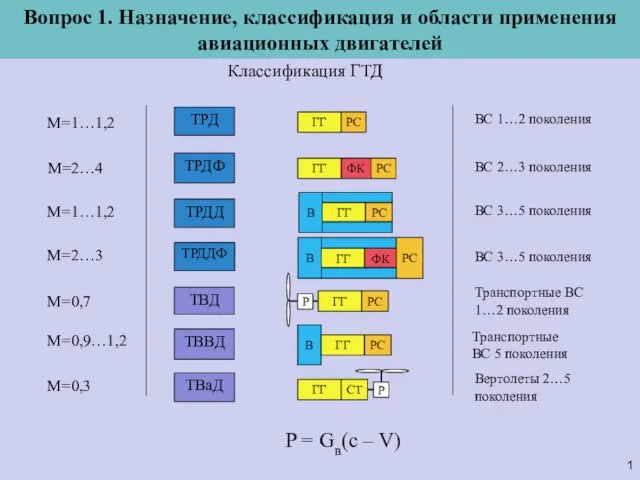 Классификация ГТД
Классификация ГТД Puzat.ru-RomanPuzat-Marafon2013-Ves
Puzat.ru-RomanPuzat-Marafon2013-Ves Ты мое счастье
Ты мое счастье Сортировка и поиск данных в электронных таблицах
Сортировка и поиск данных в электронных таблицах Совещание по проекту образование через интернет для детей инвалидов
Совещание по проекту образование через интернет для детей инвалидов Введение в управление проектами
Введение в управление проектами 364291
364291 Алгоритмы траекторной обработки данных
Алгоритмы траекторной обработки данных 20120116_yanvar
20120116_yanvar Привычки хорошие и плохие
Привычки хорошие и плохие Клоунский грим
Клоунский грим Природа и здоровье
Природа и здоровье Święty Mateusz Apostoł
Święty Mateusz Apostoł 20120506_riskuy-igra_po_istorii_-_2chast
20120506_riskuy-igra_po_istorii_-_2chast Ленточные конвейеры, виды и назначение
Ленточные конвейеры, виды и назначение 20171218_ovoshchi
20171218_ovoshchi Символика архитектуры православного храма
Символика архитектуры православного храма 20130318_religiya
20130318_religiya