Содержание
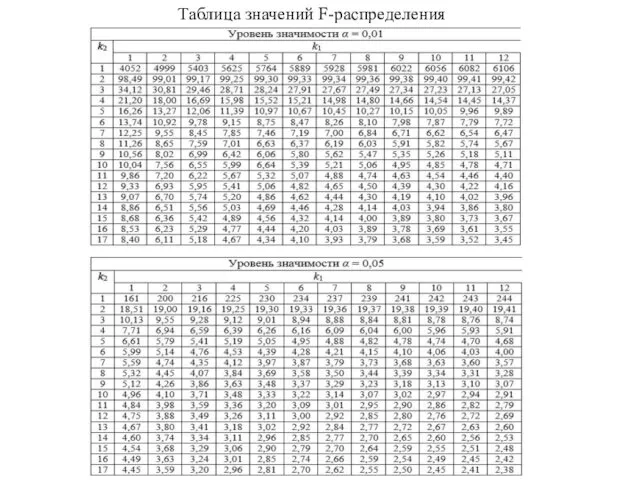
- 2. Таблица значений F-распределения
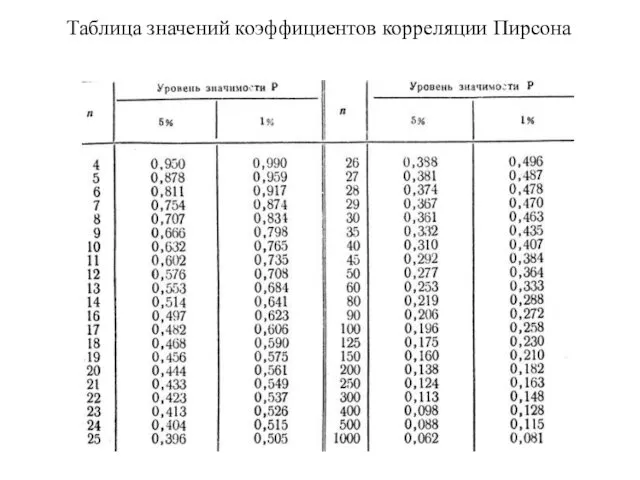
- 6. Таблица значений коэффициентов корреляции Пирсона
- 7. Проверка гипотез о равенстве дисперсий для нескольких выборок. Критерии Бартлетта и Кохрена
- 11. Примеры По четырем независимым выборкам объемами n1 = 17, n2 = 20, n3 = 15, n4
- 12. Примеры По четырем независимым выборкам объема n = 17, извлеченными из нормально распределенных генеральных совокупностей, найдены
- 13. Примеры 11. По трем независимым выборкам, объемы которых п1 = 9, п2 = 13, п3 =
- 14. Регрессионный и корреляционный анализ
- 15. Статистической зависимостью называется такая зависимость, при которой изменение одной из величин влечет за собой изменение распределения
- 16. Задача корреляционного анализа - установить, являются ли данные случайные величины взаимосвязанными. Задача регрессионного анализа - описать
- 17. Коэффициенты корреляции 1. Для порядковых данных используются следующие коэффициенты корреляции: • ρ - коэффициент ранговой корреляции
- 18. Коэффициент ранговой корреляции Спирмена Допустим, что объекты генеральной совокупности обладают двумя качественными признаками. Под качественным подразумевается
- 21. Преимущество коэффициента корреляции рангов Спирмена состоит в том, что ранжировать можно и по таким признакам, которые
- 22. Недостатки: одинаковым разностям рангов могут соответствовать совершенно отличные разности значений признаков (в случае количественных признаков); характер
- 23. Пример Два преподавателя оценили знания 12 учащихся по стобалльной системе и выставили им следующие оценки (в
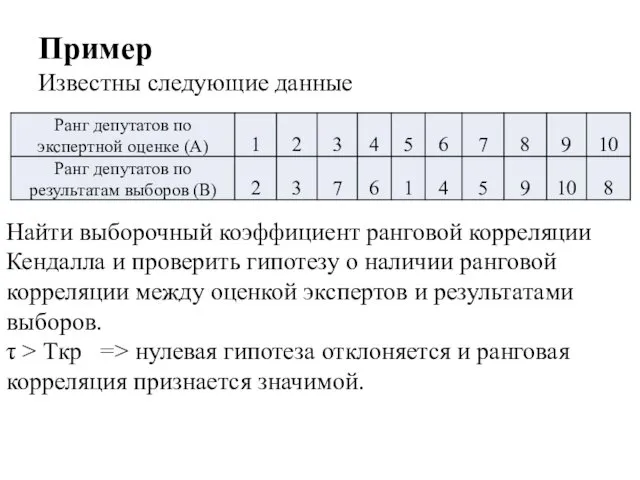
- 28. Пример Известны следующие данные Найти выборочный коэффициент ранговой корреляции Кендалла и проверить гипотезу о наличии ранговой
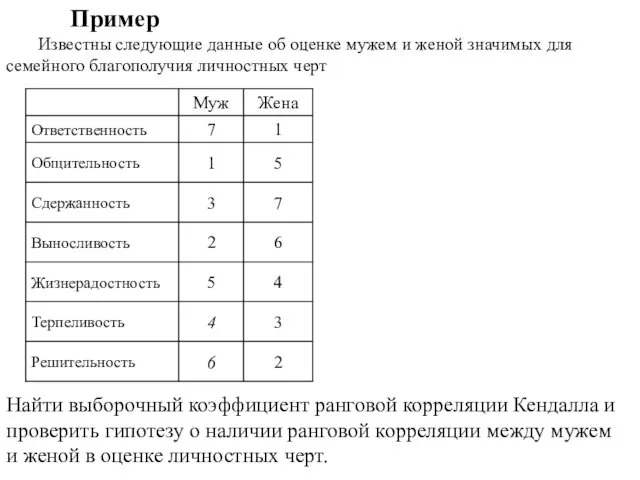
- 29. Пример Известны следующие данные об оценке мужем и женой значимых для семейного благополучия личностных черт Найти
- 30. Коэффициент корреляции Пирсона Для применения коэффициента корреляции Пирсона, необходимо соблюдать следующие условия: Сравниваемые переменные должны быть
- 33. Пример При уровне значимости 0,05
- 34. Пример В некоторой стране годовой доход каждого индивида у определяется по формуле: у = 10000+500s +
- 35. Коэффициент частной корреляции
- 36. Парный регрессионный анализ.
- 37. Модель парной линейной регрессии y = α + βx + u Величина у, рассматриваемая как зависимая
- 38. Основные причины наличия случайной составляющей в модели парной регрессии. Невключение объясняющих переменных. Агрегирование переменных. Неправильное описание
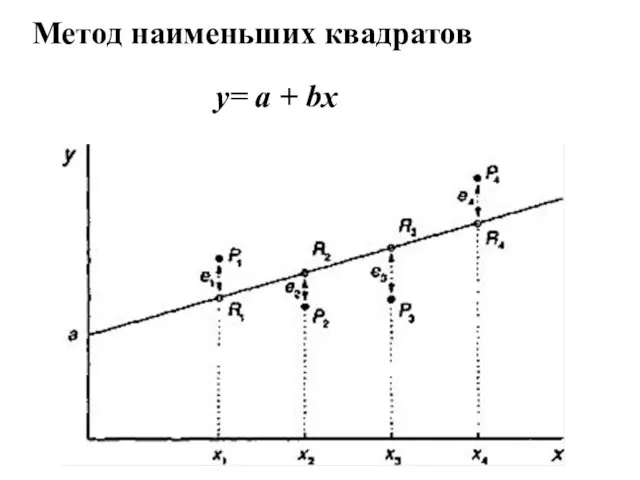
- 39. Метод наименьших квадратов y= a + bx
- 42. Скачать презентацию


































 Основы тепловидения
Основы тепловидения Что такое комбинаторика?
Что такое комбинаторика? Международный день леса
Международный день леса Родительское собрание. Календарный учебный график
Родительское собрание. Календарный учебный график Электронный журнал по дисциплине Информатика
Электронный журнал по дисциплине Информатика Prezentatsia_Lebedev
Prezentatsia_Lebedev Мамонты
Мамонты Осетровая рыба
Осетровая рыба Основные темы и герои Библии
Основные темы и герои Библии Наименование вашей темы (строго по приказу)
Наименование вашей темы (строго по приказу) мы за онлайн Татэнергосбыт
мы за онлайн Татэнергосбыт Заповеди Божии
Заповеди Божии 20111012_applikaciya_transport
20111012_applikaciya_transport Католицизм. Урок 12
Католицизм. Урок 12 Выступление Протасова
Выступление Протасова ПРЕЗЕНТАЦИЯ НЕПОСРЕДСТВЕННО ОБРАЗОВАТЕЛЬНОЙ ДЕЯТЕЛЬНОСТИВ ПОДГОТОВИТЕЛЬНОЙ ГРУППЕ НЕПОСЕДЫ
ПРЕЗЕНТАЦИЯ НЕПОСРЕДСТВЕННО ОБРАЗОВАТЕЛЬНОЙ ДЕЯТЕЛЬНОСТИВ ПОДГОТОВИТЕЛЬНОЙ ГРУППЕ НЕПОСЕДЫ Искусство на кончиках пальцев. Развитие мелкой моторики и функциональности рук у детей: традиционные и инновационные подходы
Искусство на кончиках пальцев. Развитие мелкой моторики и функциональности рук у детей: традиционные и инновационные подходы Физико-механические свойства горных пород
Физико-механические свойства горных пород Диадок. Презентация по своим типам документов
Диадок. Презентация по своим типам документов 20131210_professiya_krovelshchik_0
20131210_professiya_krovelshchik_0 Стропальщик. Федеральные нормы и правила в области промышленной безопасности
Стропальщик. Федеральные нормы и правила в области промышленной безопасности Логические основы ЭВМ
Логические основы ЭВМ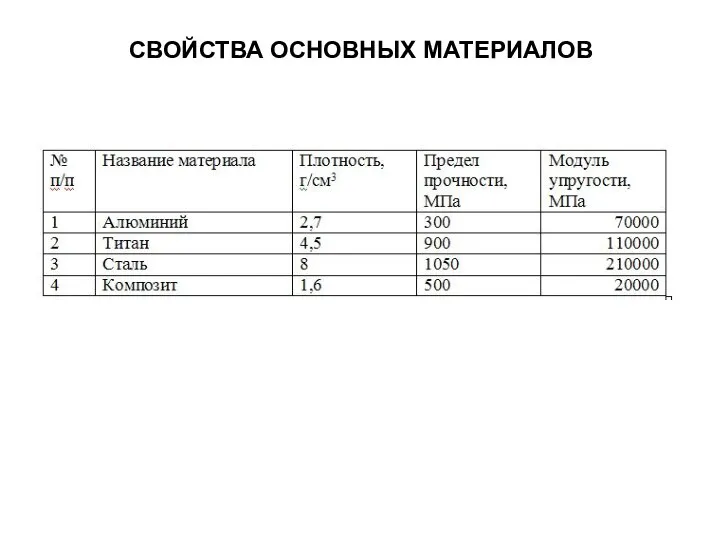 Свойства основных материалов
Свойства основных материалов Розробка та дослідження екструзійного преса з стабілізованою швидкістю бруса для виробництва будівельної кераміки
Розробка та дослідження екструзійного преса з стабілізованою швидкістю бруса для виробництва будівельної кераміки Основы рационального выбора и использования электрооборудования
Основы рационального выбора и использования электрооборудования Поэт Козлов С.Н
Поэт Козлов С.Н Скребковые конвейеры
Скребковые конвейеры сайт - копия
сайт - копия