Содержание
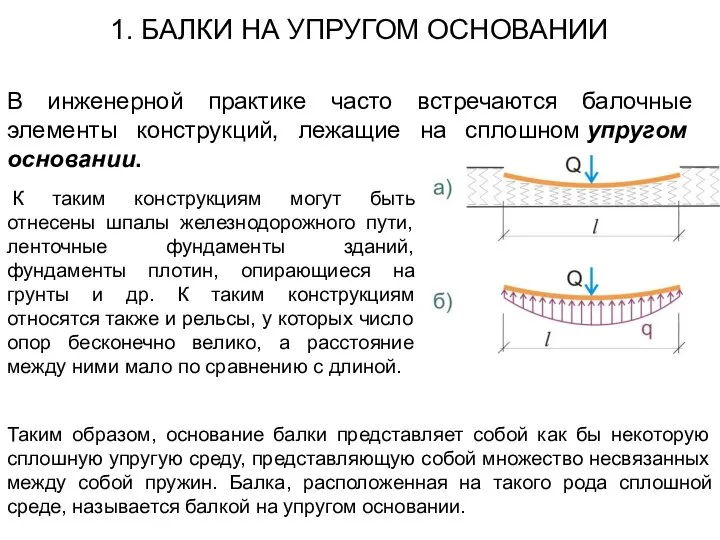
- 2. К таким конструкциям могут быть отнесены шпалы железнодорожного пути, ленточные фундаменты зданий, фундаменты плотин, опирающиеся на
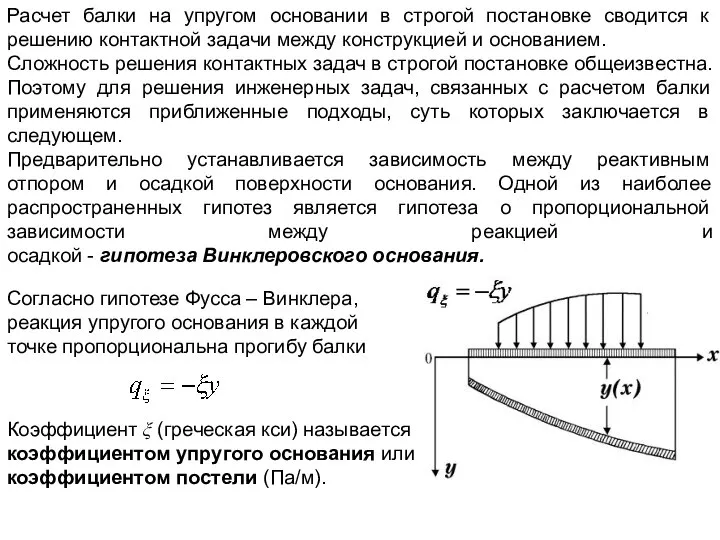
- 3. Расчет балки на упругом основании в строгой постановке сводится к решению контактной задачи между конструкцией и
- 4. Простое предположение, что непрерывная реакция основания пропорциональна прогибу, приводит к вполне удовлетворительным результатам во многих практических
- 5. 2. Расчет бесконечных балок на упругом основании Дифференциальное уравнение упругой линии балки – линейное неоднородное ДУ
- 6. Рассмотрим решение однородного дифференциального уравнения : Решаем через характеристическое уравнение: Корни характеристического уравнения: где i –
- 7. Анализируя полученный результат, приходим к выводу, что общее решение включает выражения для затухающей и возрастающей гармоник
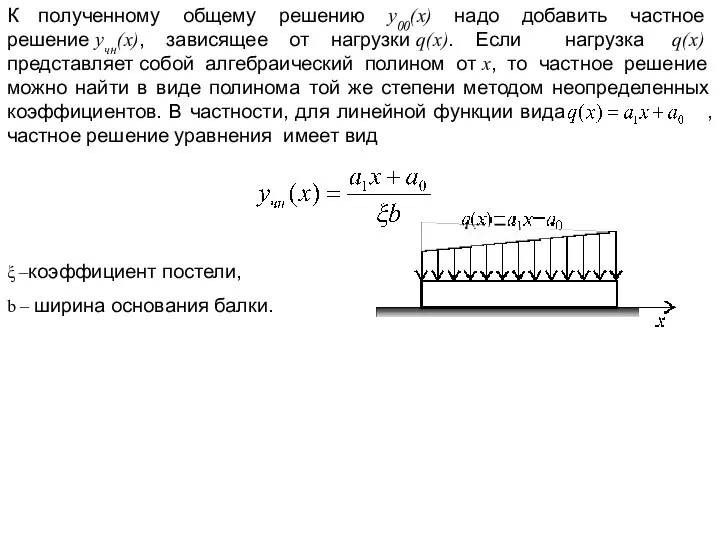
- 8. К полученному общему решению y00(x) надо добавить частное решение yчн(x), зависящее от нагрузки q(x). Если нагрузка
- 9. Рассмотрим расчет бесконечно длинной балки на упругом основании, загруженной одной силой Р Начало координат расположим под
- 10. Для определения постоянной С воспользуемся начальными условиями по центру балки, согласно им поперечная сила в правом
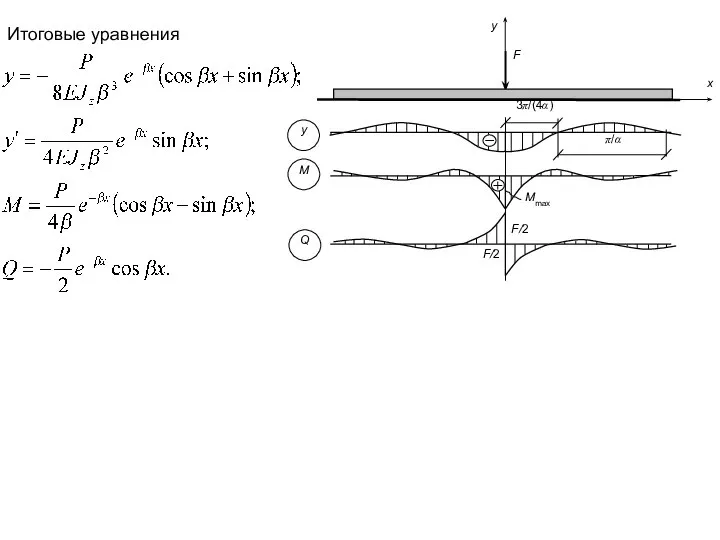
- 11. Итоговые уравнения
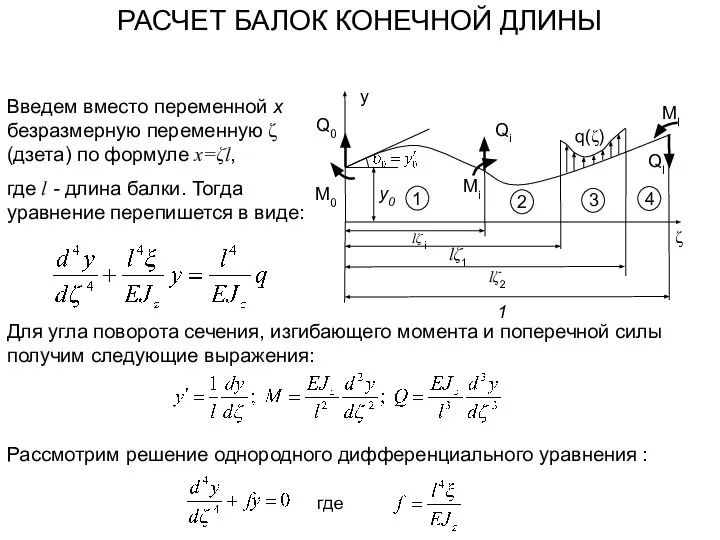
- 12. Введем вместо переменной x безразмерную переменную ζ (дзета) по формуле x=ζl, где l - длина балки.
- 13. его характеристическое уравнение: Корни характеристического уравнения: Введем обозначения: Тогда формулы для корней характеристического уравнения перепишутся в
- 14. Третья форма решения удобна для балок ограниченной длины. В данном случае возможно получение формул метода начальных
- 15. Метод начальных параметров для балок на упругом основании Исходная система уравнений будет иметь вид: При постановке
- 16. Из НУ определяем постоянные интегрирования Для упрощения записи введем функции Крылова: Функции Крылова обладают свойствами С
- 17. Для балок с несколькими приложенными сосредоточенными силами, моментами и грузовыми площадками соотношения проще записать в матричной
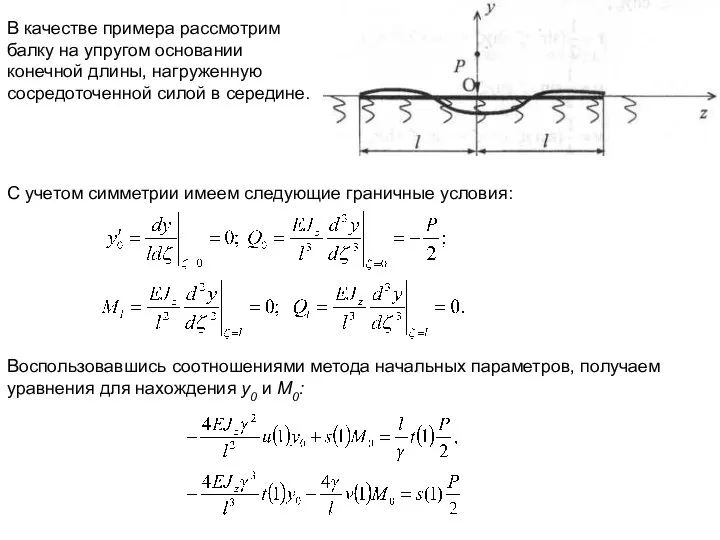
- 18. В качестве примера рассмотрим балку на упругом основании конечной длины, нагруженную сосредоточенной силой в середине. С
- 20. Скачать презентацию











 Три фактора распространения болезней
Три фактора распространения болезней  МКОУ «Кулунская оош» Акция « Я выбираю спорт как альтернативу пагубным привычкам»
МКОУ «Кулунская оош» Акция « Я выбираю спорт как альтернативу пагубным привычкам»  Разминка по экологическому праву. Подготовила студентку 2 курса юридического факультета группы Ю124Б Тужилова Л.В.
Разминка по экологическому праву. Подготовила студентку 2 курса юридического факультета группы Ю124Б Тужилова Л.В. Технология обучения в сотрудничестве на уроке английского языка (ТОСУА) Основная идея ТОСУА – создание условий для активной учеб
Технология обучения в сотрудничестве на уроке английского языка (ТОСУА) Основная идея ТОСУА – создание условий для активной учеб «Проектная деятельность учащихся» Семинар учителей МОУ СОШ № 27 пгт Смоляниново
«Проектная деятельность учащихся» Семинар учителей МОУ СОШ № 27 пгт Смоляниново Презентация "Стили и направления изобразительного искусства. ХХ век" - скачать презентации по МХК
Презентация "Стили и направления изобразительного искусства. ХХ век" - скачать презентации по МХК Строительство универсальной спортивной площадки на территории микрорайона «Южный-2» в с. Завьялово
Строительство универсальной спортивной площадки на территории микрорайона «Южный-2» в с. Завьялово Презентация на тему "Профессиональная компетентность учителя" - скачать презентации по Педагогике
Презентация на тему "Профессиональная компетентность учителя" - скачать презентации по Педагогике Қайта даму дəуірінің костюмі
Қайта даму дəуірінің костюмі армения старшая группа
армения старшая группа Презентация«Аудит документов по оформлению импортных операций»
Презентация«Аудит документов по оформлению импортных операций»  Табличка на стол (только для CI Дилеров)
Табличка на стол (только для CI Дилеров) Эволюция ЕСТЕСТВЕННОНАУЧНОЙ КАРТИНЫ МИРА. Подготовили: Кондратьев Александр Акинбани Виктория
Эволюция ЕСТЕСТВЕННОНАУЧНОЙ КАРТИНЫ МИРА. Подготовили: Кондратьев Александр Акинбани Виктория Инструкция по использованию инфомата для записи к врачу в порядке электронной очереди с помощью портала пациента
Инструкция по использованию инфомата для записи к врачу в порядке электронной очереди с помощью портала пациента Полевые транзисторы. Основные сведения и классификация
Полевые транзисторы. Основные сведения и классификация Ватутин Николай Фёдорович
Ватутин Николай Фёдорович Архитектурная климатология
Архитектурная климатология Serial Communications
Serial Communications Техническая диагностика подвижного состава
Техническая диагностика подвижного состава Тема : «Классный руководитель – архитектор классного коллектива»
Тема : «Классный руководитель – архитектор классного коллектива» Растревоженная душа В. Шукшина. К 90 – летию писателя
Растревоженная душа В. Шукшина. К 90 – летию писателя 29 ноября - День матери
29 ноября - День матери Презентация ЖК “Лефортово Парк”
Презентация ЖК “Лефортово Парк” Презентация Безопасность продовольственных и непродовольственных товаров
Презентация Безопасность продовольственных и непродовольственных товаров В мире головоломок - презентация для начальной школы_
В мире головоломок - презентация для начальной школы_ Общественный строй в виде тест-тренинга
Общественный строй в виде тест-тренинга Презентация Режим пограничной зоны, территориальных и внутренних вод
Презентация Режим пограничной зоны, территориальных и внутренних вод Степень с целым показателем. 8 класс 1.04.13
Степень с целым показателем. 8 класс 1.04.13