Содержание
- 2. «Показательная функция Неслучайно родилась В жизнь органически влилась И движением прогресса занялась!» Б.Слуцкий.
- 3. Цели и задачи: - исследовать историю числа е и расширить знания об иррациональном числе е. Задачи:
- 4. История числа е Число е иногда называют неперовым в честь шотландского учёного Непера, автора работы «Описание
- 5. Саму же константу впервые вычислил швейцарский математик Бернулли при анализе следующего предела: Первое известное использование этой
- 6. Способы определения числа е Число е можно определить несколькими способами. Рассмотрим числовую последовательность с общим членом
- 7. Подробнее о пределе Этот предел называется вторым замечательным пределом. Число е приблизительно равно 2,718281828459045…(приложение 1) Эйлеру
- 8. Для быстрого вычисления большого числа знаков удобнее использовать другое разложение: Число е можно записать в виде
- 9. Число e играет огромную роль в математике, физике, астрономии и других науках. Вот некоторые вопросы, при
- 10. Рассмотрим пример Рост клеток Число Эйлера действительно имеет огромное значение как в математике, так и в
- 12. Скачать презентацию
«Показательная функция
Неслучайно родилась
В жизнь органически влилась
И движением прогресса занялась!»
Б.Слуцкий.
«Показательная функция
Неслучайно родилась
В жизнь органически влилась
И движением прогресса занялась!»
Б.Слуцкий.
Цели и задачи:
- исследовать историю числа е и расширить знания об иррациональном
Цели и задачи:
- исследовать историю числа е и расширить знания об иррациональном
История числа е
Число е иногда называют неперовым в честь шотландского учёного Непера, автора работы
История числа е
Число е иногда называют неперовым в честь шотландского учёного Непера, автора работы
Саму же константу впервые вычислил швейцарский математик Бернулли при анализе следующего предела:
Первое
Саму же константу впервые вычислил швейцарский математик Бернулли при анализе следующего предела: Первое
Способы определения числа е
Число е можно определить несколькими способами.
Рассмотрим числовую последовательность
Способы определения числа е
Число е можно определить несколькими способами. Рассмотрим числовую последовательность
Подробнее о пределе
Этот предел называется вторым замечательным пределом.
Число е приблизительно равно
Подробнее о пределе
Этот предел называется вторым замечательным пределом. Число е приблизительно равно
Для быстрого вычисления большого числа знаков удобнее использовать другое разложение:
Число
Для быстрого вычисления большого числа знаков удобнее использовать другое разложение: Число
Число e играет огромную роль в математике, физике, астрономии и других науках. Вот
Число e играет огромную роль в математике, физике, астрономии и других науках. Вот
Рассмотрим пример
Рост клеток Число Эйлера действительно имеет огромное значение как
Рассмотрим пример
Рост клеток Число Эйлера действительно имеет огромное значение как









 Презентация "Питер Пауль Рубенс (1577-1640)" - скачать презентации по МХК
Презентация "Питер Пауль Рубенс (1577-1640)" - скачать презентации по МХК Бухгалтерский учет процессов Выделяют три процесса работы предприятия: Снабжение (заготовки, закупки) → сырье и материалы как часть материально-производственных запасов (МПЗ) Производство → себестоимость (затраты) Продажа (реализация) → готовая проду
Бухгалтерский учет процессов Выделяют три процесса работы предприятия: Снабжение (заготовки, закупки) → сырье и материалы как часть материально-производственных запасов (МПЗ) Производство → себестоимость (затраты) Продажа (реализация) → готовая проду Презентация "Возникновение барокко" - скачать презентации по МХК
Презентация "Возникновение барокко" - скачать презентации по МХК 10 самых красивых мечетей мира
10 самых красивых мечетей мира Философия Допетровской Руси Выполнили: СТУДЕНТЫ 1 КУРСА фтд ГРУППЫ Тс 02/1407 Алексеева Дарья АГафонов Сергей
Философия Допетровской Руси Выполнили: СТУДЕНТЫ 1 КУРСА фтд ГРУППЫ Тс 02/1407 Алексеева Дарья АГафонов Сергей Философия управления персоналом
Философия управления персоналом Моя история в Medialab
Моя история в Medialab Introduction to graphs
Introduction to graphs ОФИЦИЈАЛНА ПРОМОЦИЈА
ОФИЦИЈАЛНА ПРОМОЦИЈА Welcome To Medland
Welcome To Medland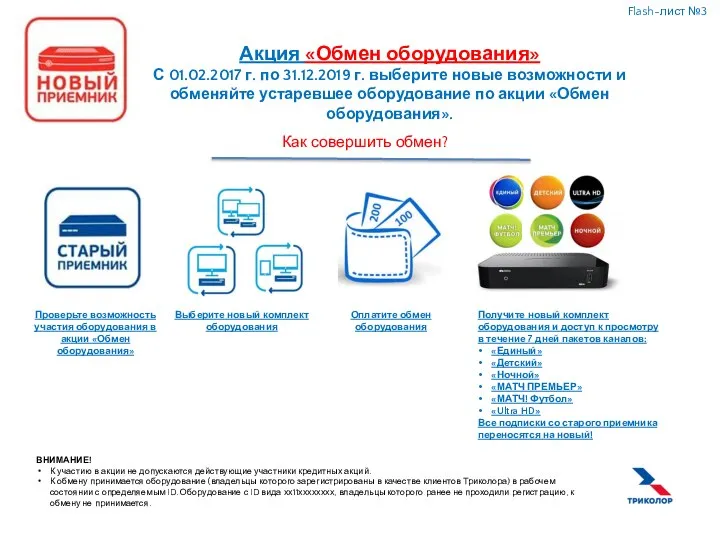 Акция «Обмен оборудования»
Акция «Обмен оборудования» Рождественская елка Tannenbaum
Рождественская елка Tannenbaum Способы пломбирования при лечении пульпита
Способы пломбирования при лечении пульпита  критерии оценки заключения: допустимость, относительность, достоверность и доказательность Терешкова М. ДС5 ФТД 5
критерии оценки заключения: допустимость, относительность, достоверность и доказательность Терешкова М. ДС5 ФТД 5 Коренные народы России
Коренные народы России Архитектурные конструкции малоэтажных зданий
Архитектурные конструкции малоэтажных зданий Религиозное сознание
Религиозное сознание Интегрированный урок по чтению и письму в 1 классе Учитель начальных классов МОУ «Подолешенская СОШ» Стрельникова Галина Ивано
Интегрированный урок по чтению и письму в 1 классе Учитель начальных классов МОУ «Подолешенская СОШ» Стрельникова Галина Ивано Classification of computer
Classification of computer Монархическая форма правления
Монархическая форма правления Презентация "Снежинки" - скачать презентации по МХК
Презентация "Снежинки" - скачать презентации по МХК How did we make the biggest game on Defold in 1 year
How did we make the biggest game on Defold in 1 year Unix/Linux commands and shell programming
Unix/Linux commands and shell programming Формы и виды социальной ответственности современного бизнеса
Формы и виды социальной ответственности современного бизнеса DeVita Energy mini - цифровое устройство оздоровления
DeVita Energy mini - цифровое устройство оздоровления Методы. Синтаксис метода
Методы. Синтаксис метода Фразеология
Фразеология ОТКРЫТКА ДЛЯ ПАПЫ Работа с бумагой
ОТКРЫТКА ДЛЯ ПАПЫ Работа с бумагой