Содержание
- 2. Математическое ожидание д.сл.в. Определение Математическим ожиданием Mξ сл. вел. ξ с дискретным распределением, задаваемым законом распределения
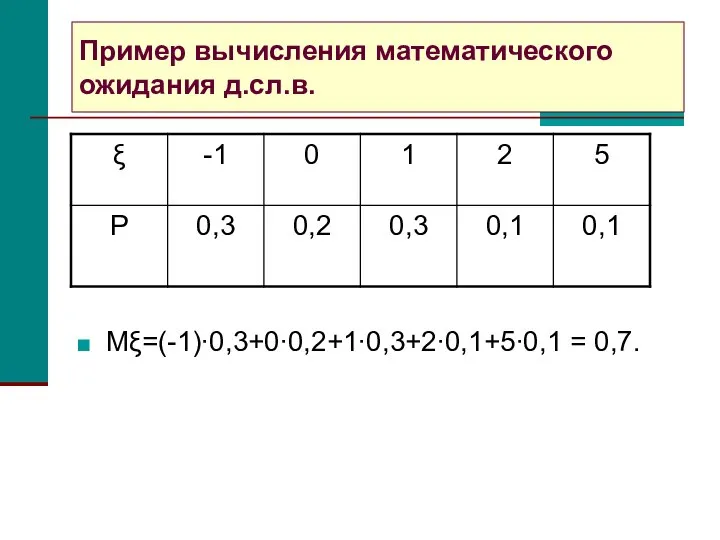
- 3. Пример вычисления математического ожидания д.сл.в. Mξ=(-1)∙0,3+0∙0,2+1∙0,3+2∙0,1+5∙0,1 = 0,7.
- 4. Математическим ожиданием Mξ сл. в. ξ с абсолютно непрерывным распределением с плотностью распределения fξ(x) называется число
- 5. Замечание Если то говорят, что математическое ожидание не существует.
- 6. Математическое ожидание функции дискретной случайной величины Математическим ожиданием функции φ(ξ) дискретной случайной величины ξ, имеющей распределение
- 7. Математическое ожидание функции непрерывной случайной величины Математическое ожидание функции непрерывной случайной величины с плотностью вероятностей fξ
- 8. Свойства матожидания 1. MC = C, (С = const ) 2. M(Cξ) = C∙Mξ, 3. M(ξ
- 9. Дисперсия случайной величины Определение. Если случайная величина ξ имеет математическое ожидание M ξ , то дисперсией
- 10. Свойства дисперсии Дисперсия любой случайной величины неотрицательна, Dξ ≥ 0; Дисперсия константы равна нулю, Dc =
- 11. Свойства дисперсии Еще одно важное свойство дисперсии
- 12. Вычисление дисперсии Для вычисления дисперсии надо найти Mξ2 и отнять квадрат математического ожидания, Dξ = Mξ2
- 13. Вычисление Mξ2
- 14. Пример вычисления дисперсии Mξ2=(-1)2∙0,3+02∙0,2+12∙0,3+22∙0,1+52∙0,1 = 3,5. Mξ = 0,7. Dξ = 3,5 – (0,7)2 = 3,01.
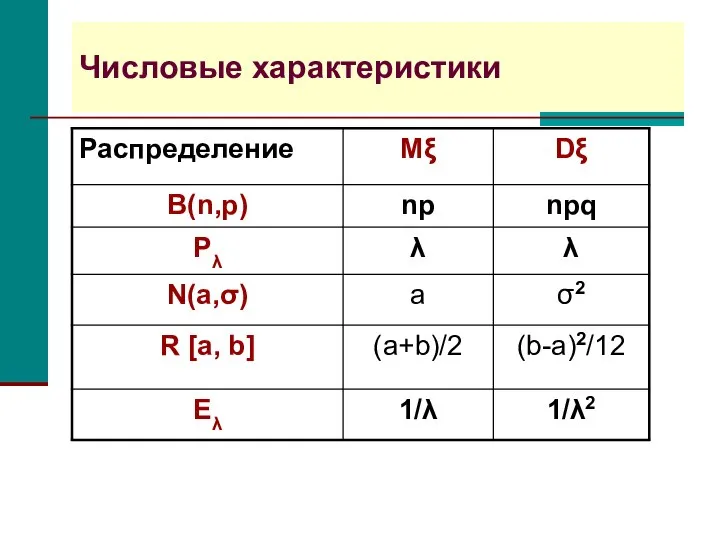
- 15. Числовые характеристики
- 16. Пример
- 17. Начальные и центральные моменты Определение. Начальным моментом k-го порядка случайной величины ξ называется математическое ожидание k-й
- 18. Среднеквадратичное отклонение Для определения меры разброса значений случайной величины часто используется среднеквадратичное отклонение σξ, связанное с
- 19. Замечания 1. Математическое ожидание случайной величины - начальный момент первого порядка, α1 = Mξ1. 2. Дисперсия
- 20. Коэффициент асимметрии Определение. Коэффициентом асимметрии называется число A, которое определяется формулой где μ3 - центральный момент
- 21. Замечания У симметричного распределения асимметрия равна 0. Асимметрия распределения с длинным правым хвостом положительна. Если распределение
- 22. Пример: A
- 23. Пример: A > 0
- 24. Коэффициент эксцесса Определение. Коэффициентом эксцесса называется число Е, которое определяется формулой
- 25. Замечания Коэффициент эксцесса указывает на «островершинность» или «плосковершинность» графика плотности. Если Е > 0, то это
- 26. Пример: E > 0
- 27. Мода Определение. Модой непрерывной случайной величины ξ называется значение m0, при котором плотность fξ(x) достигает максимума.
- 28. Пример Мода m0 дискретной случайной величины ξ равна значению ξ = 1, т.к. p(ξ = 1)=
- 29. Медиана Определение. Медианой непрерывной случайной величины ξ называется значение me, при котором F(me) = 1/2. Замечание.
- 30. Чтобы найти медиану, надо решить уравнение Корень этого уравнения и есть медиана. (Если корней несколько, выберите
- 31. Пример. Найти медиану показательного р-я E4
- 32. Пример: мода, медиана и Mξ m0 = 8; me = 9,34; Mξ = 10.
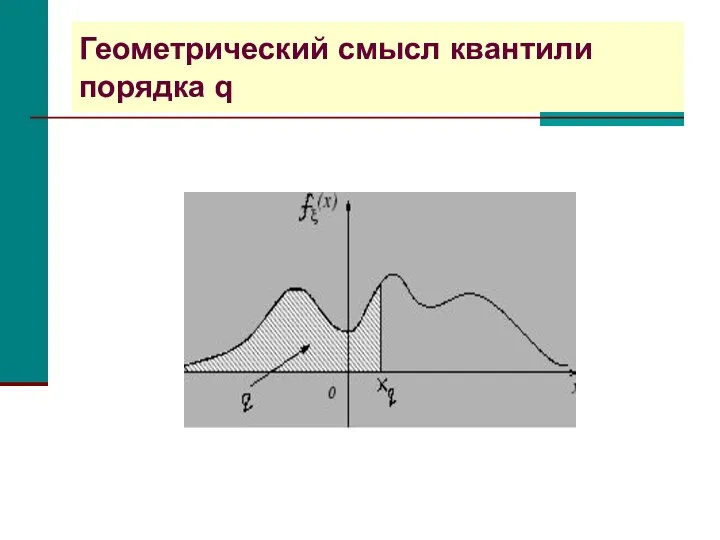
- 33. Квантиль порядка q Определение. Квантилью порядка q, 0 случайной величины ξ называется значение xq, при котором
- 34. Геометрический смысл квантили порядка q
- 35. Чтобы найти квантиль xq, надо решить уравнение Корень этого уравнения и есть квантиль порядка q. (Если
- 37. Скачать презентацию






























 Малинина Алена Викторовна Учитель черчения и изобразительного искусства МОУ « СОШ № 12» город Усолье-Сибирс
Малинина Алена Викторовна Учитель черчения и изобразительного искусства МОУ « СОШ № 12» город Усолье-Сибирс Прием документации и зачисление в организации образования
Прием документации и зачисление в организации образования Ваш праздник
Ваш праздник Компьютерные сети
Компьютерные сети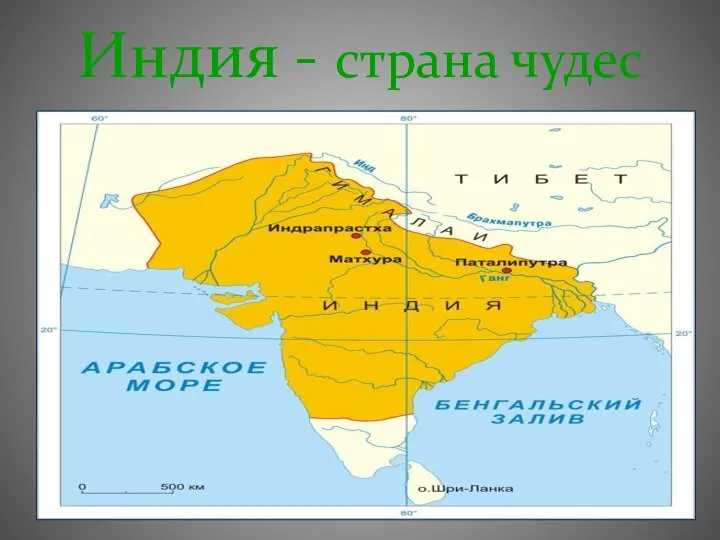 Культура Древней Индии
Культура Древней Индии Учитель английского языка Евсюкова И.А. МОУ «Федчёвская ООШ» 2009 год
Учитель английского языка Евсюкова И.А. МОУ «Федчёвская ООШ» 2009 год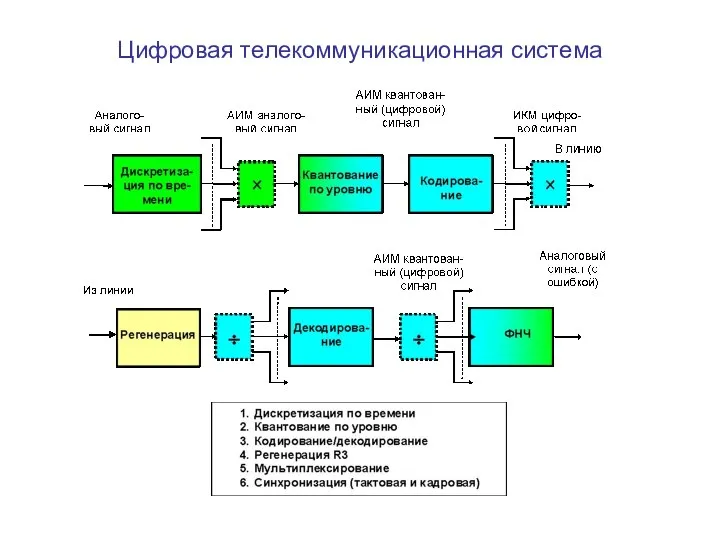 Цифровая телекоммуникационная система
Цифровая телекоммуникационная система Понятие гражданского права, как отрасли права. Источники гражданского права
Понятие гражданского права, как отрасли права. Источники гражданского права Передача информации. Локальные компьютерные сети
Передача информации. Локальные компьютерные сети Плазмозаменители
Плазмозаменители Амнистия. Помилование.Судимость.
Амнистия. Помилование.Судимость. Классы
Классы  Вода и водные устройства
Вода и водные устройства Проект по продвижению комплекса ГТО
Проект по продвижению комплекса ГТО Презентация на тему "Образовательные программы" - скачать презентации по Педагогике
Презентация на тему "Образовательные программы" - скачать презентации по Педагогике Сервисы в Android
Сервисы в Android Элементарные функции
Элементарные функции Компьютерные вирусы
Компьютерные вирусы «МЫ ВЫБИРАЕМ ЗДОРОВЬЕ!!!» «Скажи наркотикам НЕТ !!!» Один мыслитель гулял со своими учениками в саду и отвечал на их вопросы. Потом к
«МЫ ВЫБИРАЕМ ЗДОРОВЬЕ!!!» «Скажи наркотикам НЕТ !!!» Один мыслитель гулял со своими учениками в саду и отвечал на их вопросы. Потом к  XXIII Зимние Олимпийские игры
XXIII Зимние Олимпийские игры Модель методической работы школы на 2011-2012 гг. Цели: активизировать методическую работу школы способствовать повышению професс
Модель методической работы школы на 2011-2012 гг. Цели: активизировать методическую работу школы способствовать повышению професс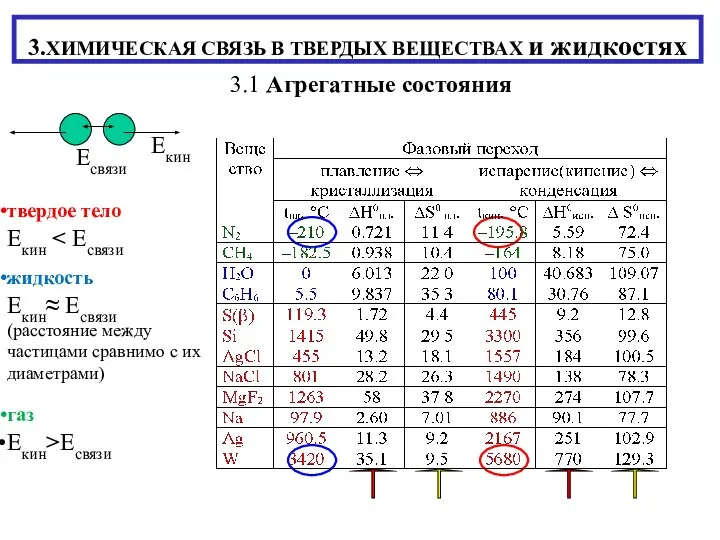 ХИМИЧЕСКАЯ СВЯЗЬ В ТВЕРДЫХ ВЕЩЕСТВАХ и жидкостях
ХИМИЧЕСКАЯ СВЯЗЬ В ТВЕРДЫХ ВЕЩЕСТВАХ и жидкостях Содержание и ремонт цементобетонных покрытий
Содержание и ремонт цементобетонных покрытий Презентация_____
Презентация_____ Разгледайте изразите. В какъв ред ще се извършват действията? Пресметнете ги. 516 – 7. 9 = 115 + 65 : 5 = 1 205. 78 – 96 : 2 = 2 015. 2 – 3 348 : 31 = - презента
Разгледайте изразите. В какъв ред ще се извършват действията? Пресметнете ги. 516 – 7. 9 = 115 + 65 : 5 = 1 205. 78 – 96 : 2 = 2 015. 2 – 3 348 : 31 = - презента Конституционное право РФ
Конституционное право РФ Укажите, в каком случае слово употреблено в прямом значении, а в каком – в переносном. Подберите и запишите синонимы к данным слова
Укажите, в каком случае слово употреблено в прямом значении, а в каком – в переносном. Подберите и запишите синонимы к данным слова Презентация на тему "Управление качество образования в МОУ Лебяженской СОШ Краснотуранского района" - скачать презентации по
Презентация на тему "Управление качество образования в МОУ Лебяженской СОШ Краснотуранского района" - скачать презентации по