Содержание
- 2. Одномерные случайные величины Пусть есть случайный эксперимент, Ω ─ пространство элементарных событий. Определение Случайной величиной ξ
- 3. Дискретные распределения Определение Случайная величина ξ имеет дискретное распределение, если она принимает не более чем счетное
- 4. Определение Если случайная величина ξ имеет дискретное распределение, то рядом распределения называется соответствие ai ↔pi, которое
- 5. Пример Подбрасываем 1 раз кубик. Пусть Ω={1,2,3,4,5,6}, и две функции из Ω в R заданы так:
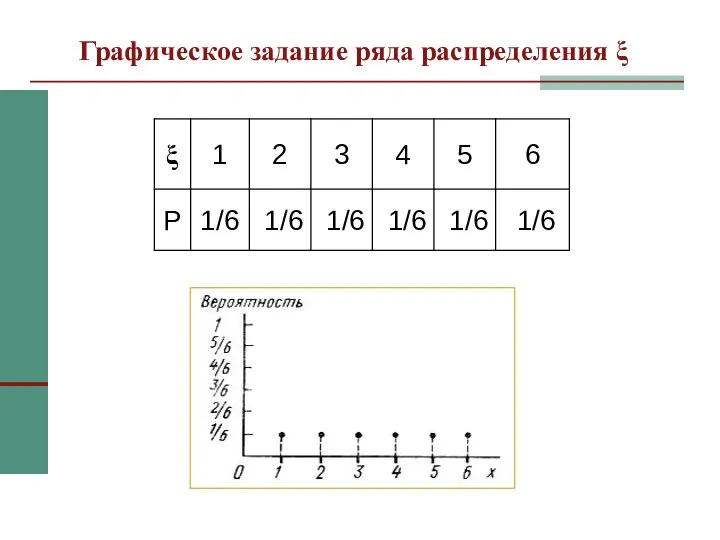
- 6. Графическое задание ряда распределения ξ
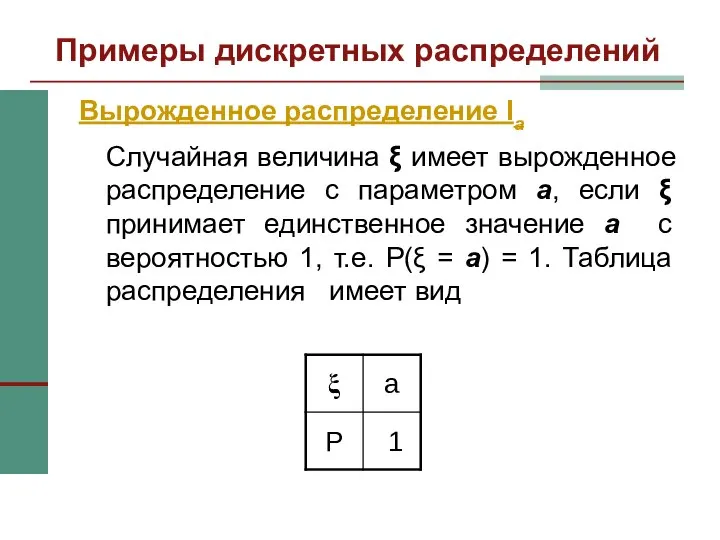
- 7. Примеры дискретных распределений Вырожденное распределение Ia Случайная величина ξ имеет вырожденное распределение с параметром a, если
- 8. Дискретное равномерное распределение Случайная величина ξ имеет дискретное равномерное распределение, если ξ принимает n значений х1,
- 9. Распределение Бернулли Bp Случайная величина ξ имеет распределение Бернулли с параметром p, если ξ принимает значения
- 10. Биномиальное распределение B(n,p) Случайная величина ξ имеет биномиальное распределение с параметрами n и p, где 0
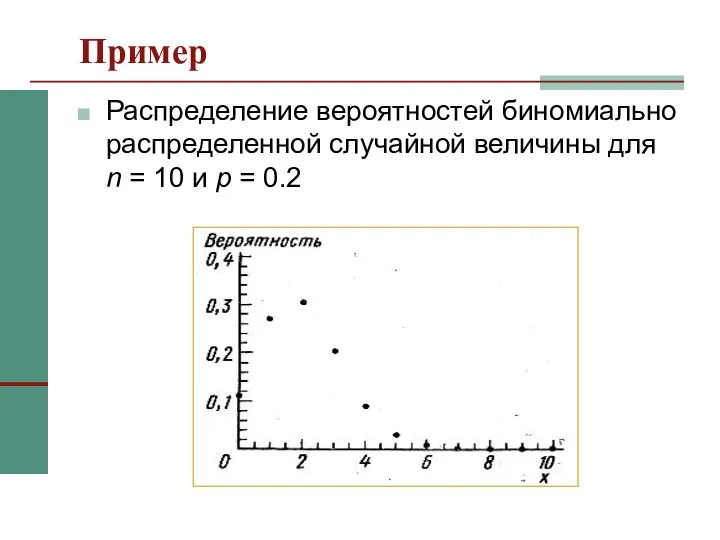
- 11. Пример Распределение вероятностей биномиально распределенной случайной величины для n = 10 и p = 0.2
- 12. Геометрическое распределение Gp, Сл.в. ξ имеет геометрическое распределение с параметром p, где 0≤p≤1, если ξ принимает
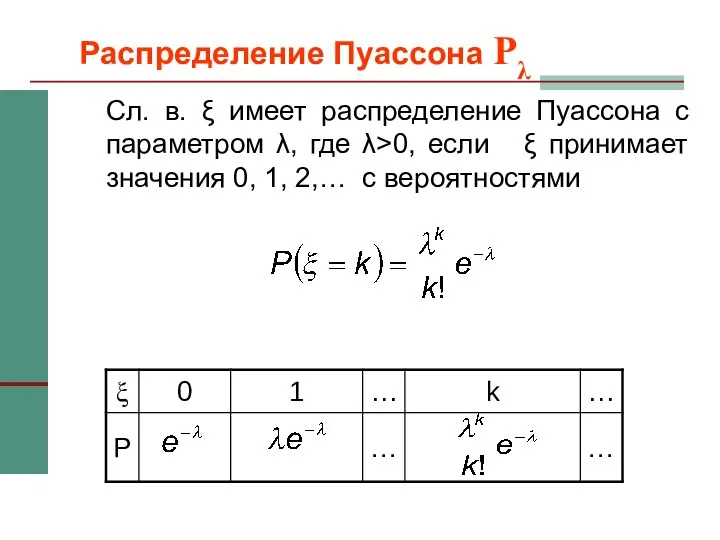
- 13. Распределение Пуассона Pλ Сл. в. ξ имеет распределение Пуассона с параметром λ, где λ>0, если ξ
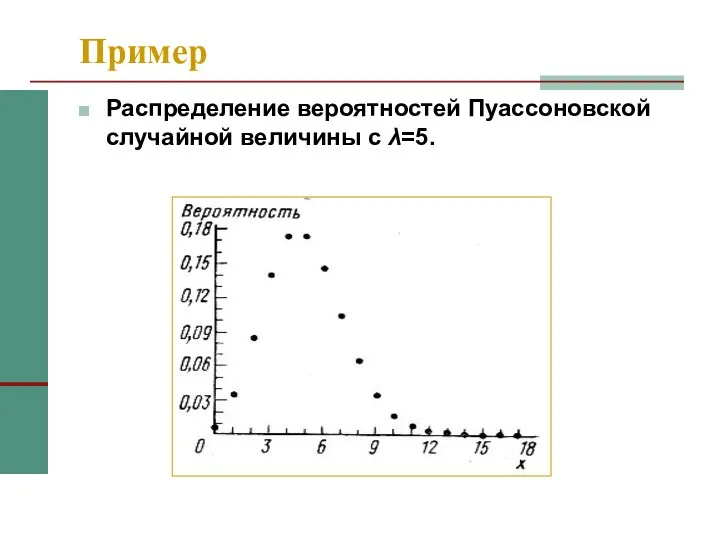
- 14. Пример Распределение вероятностей Пуассоновской случайной величины с λ=5.
- 15. Распределение Пуассона Это одно из важнейших дискретных вероятностных распределений впервые было исследовано в 1837 г. С.Пуассоном
- 16. Распределение Пуассона Примерами могут служить число частиц радиоактивного распада, зарегистрированных счетчиком в течении некоторого времени t,
- 17. Гипергеометрическое распределение Сл.в. ξ имеет гипергеометрическое распределение с параметрами n, N и K, где n ≤
- 18. Функция распределения Определение Функцией распределения случайной величины ξ называется функция Fξ(x), при каждом x∈R равная Fξ(x)
- 19. Пример
- 20. Функция распределения ξ
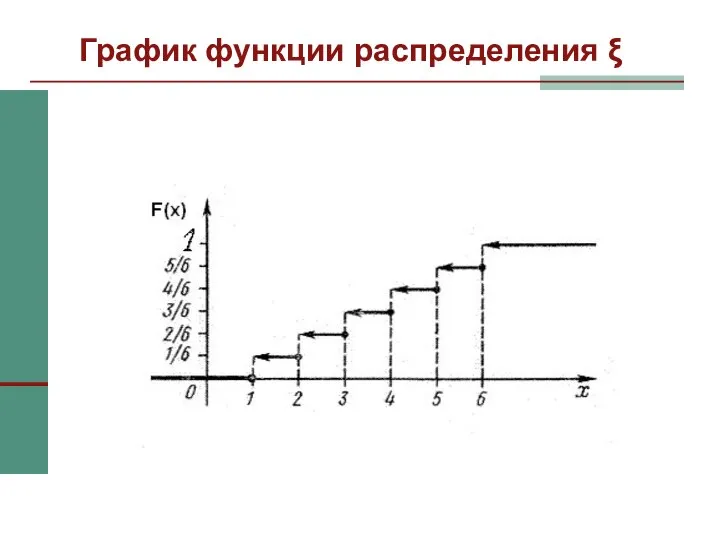
- 21. График функции распределения ξ
- 22. Свойства функции распределения 1) Функция распределения Fξ(x) не убывает: если x1 2) Существуют пределы 3) Функция
- 23. Непрерывные распределения Определение Случайная величина ξ имеет абсолютно непрерывное распределение, если существует неотрицательная функция fξ(x) такая,
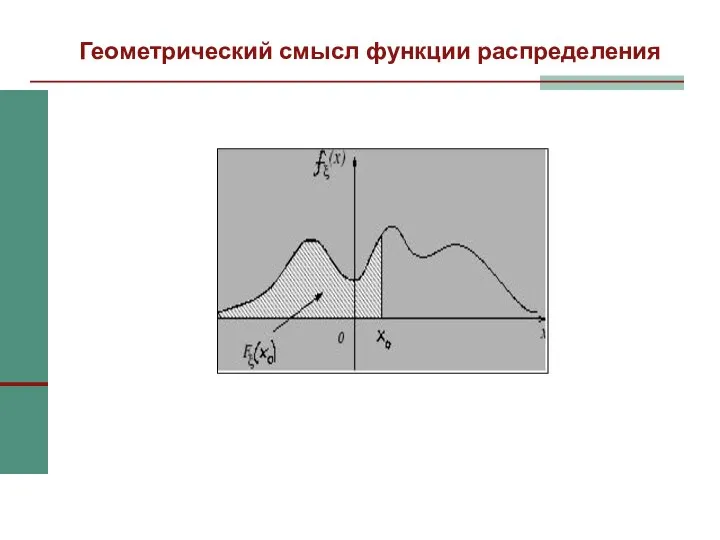
- 24. Геометрический смысл функции распределения
- 25. Свойства плотности
- 26. Замечание Термин для «почти всех» означает «для всех, кроме (возможно) x из некоторого множества нулевой меры
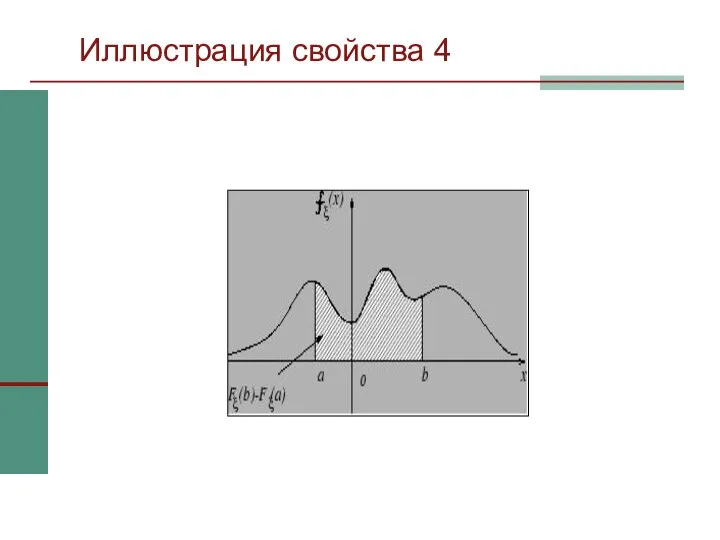
- 27. Иллюстрация свойства 4
- 28. Примеры непрерывных распределений Равномерное распределение R [a, b]
- 29. График плотности распределения R[a,b]
- 30. График функции распределения R[a,b]
- 31. С помощью линейного преобразования приводится к равномерному распределению на отрезке [0,1]. Равномерное распределение является непрерывным аналогом
- 32. Нормальное распределение N (a,σ)
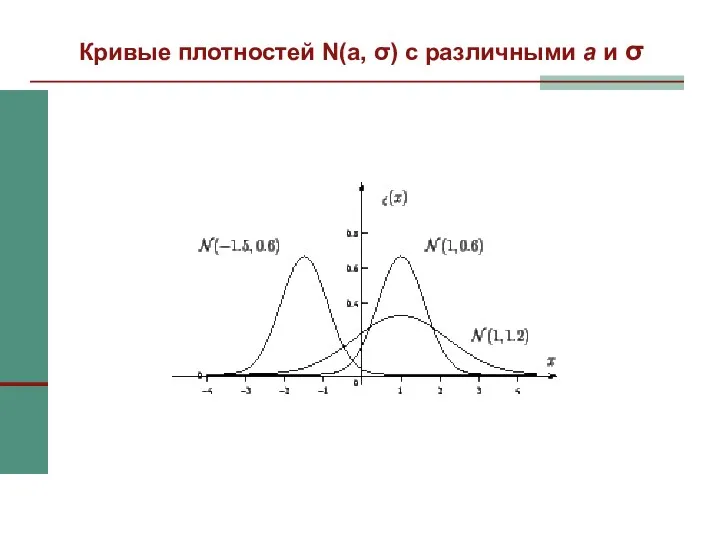
- 33. Кривые плотностей N(a, σ) с различными а и σ
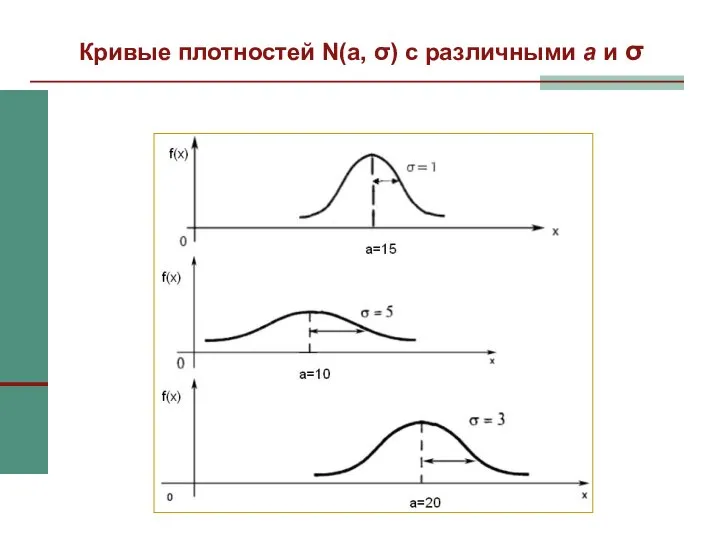
- 34. Нормальное распределение N (a,σ) Графики нормальных плотностей имеют симметричную, колоколообразную форму. а – это величина, которая
- 35. Кривые плотностей N(a, σ) с различными а и σ
- 36. Интерпретация С помощью модели нормального распределения можно описать множество явлений, например распределение высоты деревьев, площадей садовых
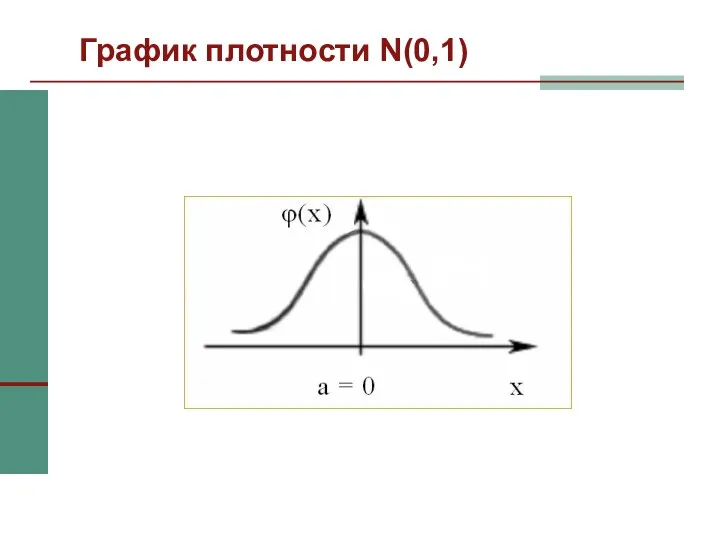
- 37. N(0,1) При а = 0 и σ = 1 нормальное распределение называют стандартным нормальным распределением
- 38. График плотности N(0,1)
- 39. Плотность и функция распределения N(0,1)
- 40. Нормальное распределение N (a, σ) Фундаментальная роль, которую играет нормальное распределение, объясняется тем, что при широких
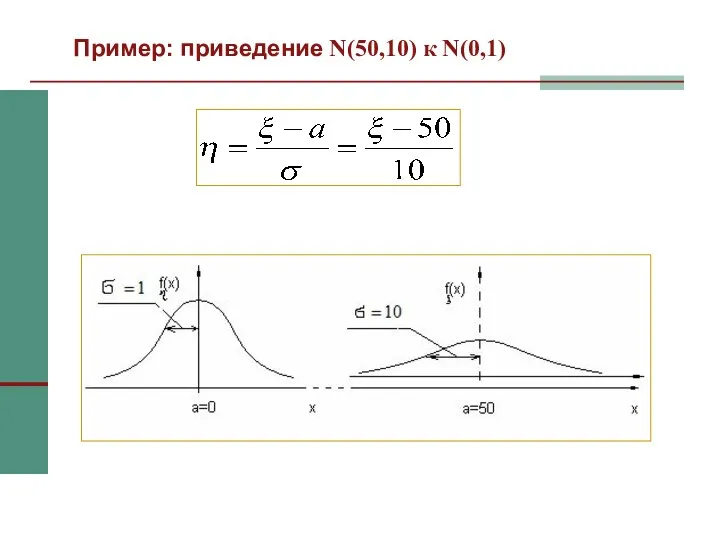
- 41. Пример: приведение N(50,10) к N(0,1)
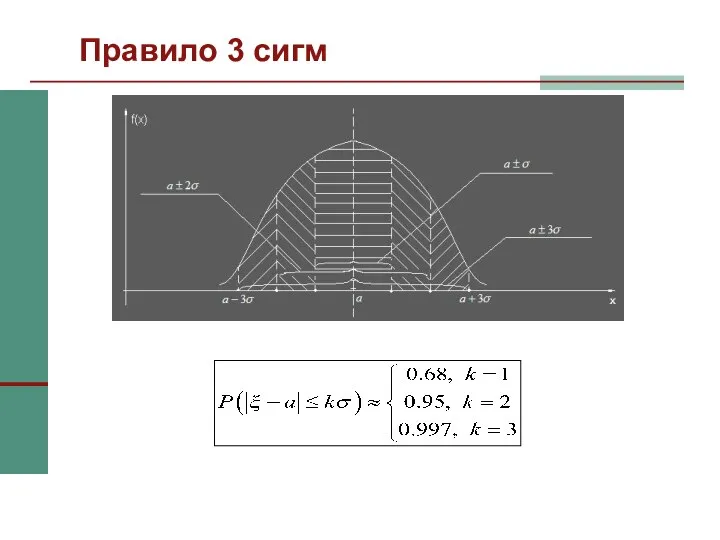
- 42. Правило 3 сигм Нормально распределенная случайная величина с большой вероятностью принимает значения, близкие к своему математическому
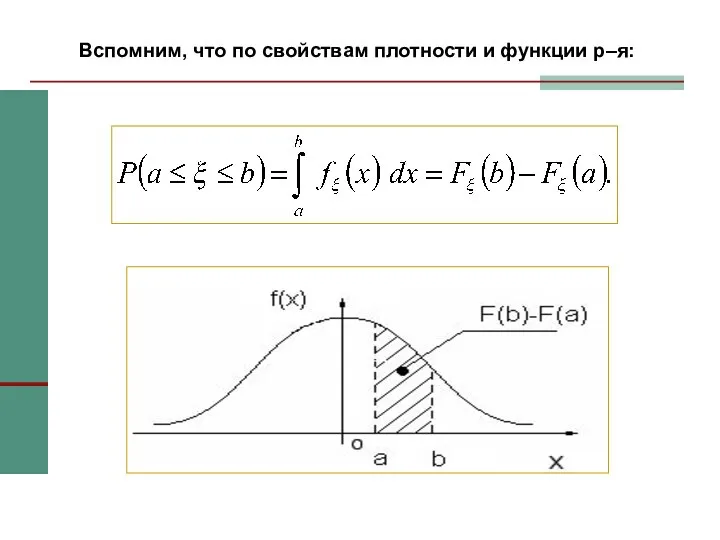
- 43. Вспомним, что по свойствам плотности и функции р–я:
- 44. Правило 3 сигм
- 45. Показательное (экспоненциальное) распределение Eλ Плотность и функция распределения Eλ
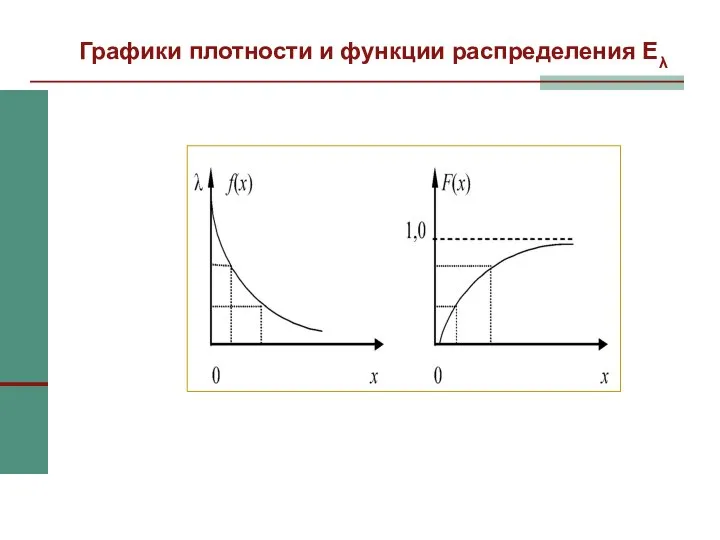
- 46. Графики плотности и функции распределения Eλ
- 47. Графики плотности и функции распределения E2
- 48. Свойства распределения Eλ Это распределение является непрерывным аналогом геометрического распределения. Обладает свойством отсутствия последействия в связи
- 49. Плотность распределения Коши Распределение Коши
- 50. Плотность Гамма –распределения Г –распределение
- 51. Гамма –распределение Г–распределение является непрерывным аналогом отрицательного биномиального распределения. При α = 1 совпадает с показательным.
- 52. Плотность распределения Лапласа Распределение Лапласа (двойное экспоненциальное распределение)
- 53. Многомерные СВ Определение n – мерной случайной величиной ξ называется вектор ξ(ω)=(ξ1(ω), ξ2(ω), … , ξn(ω)),
- 54. Определение Функцией распределения n–мерной случайной величины ξ называется функция Fξ1,ξ2,…,ξn(x1, x2, …, xn)= =P(ξ1
- 55. Свойства функции распределения 1) 0 ≤ Fξ1,ξ2,…,ξn(x1,x2,…,xn) ≤ 1, 2) Существуют пределы 3) Функция распределения Fξ(x)
- 56. Определение Случайная величина ξ имеет непрерывное n –мерное распределение, если существует неотрицательная функция fξ1,ξ2,…,ξn(x1,x2,…,xn) такая, что
- 58. Скачать презентацию


















![Примеры непрерывных распределений Равномерное распределение R [a, b]](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/1293209/slide-27.jpg)
![График плотности распределения R[a,b]](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/1293209/slide-28.jpg)
![График функции распределения R[a,b]](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/1293209/slide-29.jpg)
![С помощью линейного преобразования приводится к равномерному распределению на отрезке [0,1].](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/1293209/slide-30.jpg)


















 Электрические машины. Регулирование вторичного напряжения трансформаторов. (Лекция 8)
Электрические машины. Регулирование вторичного напряжения трансформаторов. (Лекция 8) Строки. Лекция 4
Строки. Лекция 4 Презентация Таможенные органы как функциональная система и система управления
Презентация Таможенные органы как функциональная система и система управления  Тема 1.1. Организационно-правовые формы коммерческих организаций. Правовое положение государственных и м муниципальных унита
Тема 1.1. Организационно-правовые формы коммерческих организаций. Правовое положение государственных и м муниципальных унита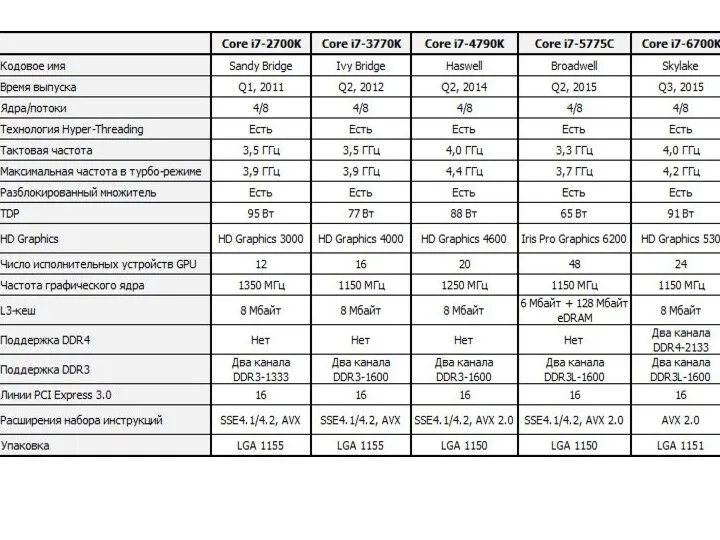 SYSmark 2014. Тестирование процессоров
SYSmark 2014. Тестирование процессоров Презентация основные понятия и определения управления в таможенных органах
Презентация основные понятия и определения управления в таможенных органах  Жизнь_ первобытных_ людей
Жизнь_ первобытных_ людей Функция Руководства. Лидерство
Функция Руководства. Лидерство Конституционное право Федеративной республики Германия (ФРГ)
Конституционное право Федеративной республики Германия (ФРГ) 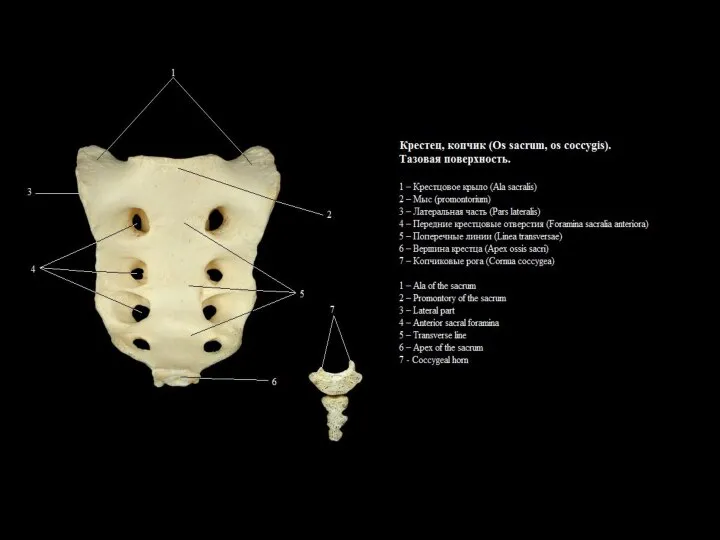 Нижняя конечность
Нижняя конечность  Иконы Богоматери: художественный метод написания Урок МХК в 10 классе Учитель Лазаренко Ирина Александровна
Иконы Богоматери: художественный метод написания Урок МХК в 10 классе Учитель Лазаренко Ирина Александровна Геополитические аспекты революционных событий 1917 г. в России
Геополитические аспекты революционных событий 1917 г. в России Специальные (юридические) гарантии
Специальные (юридические) гарантии Корень n-ой степени «Никогда не считай, что ты знаешь всё, что тебе уже больше нечему учиться». Н.Д. Зелинский
Корень n-ой степени «Никогда не считай, что ты знаешь всё, что тебе уже больше нечему учиться». Н.Д. Зелинский  Аттестационная работа. Место информационно-коммуникативных технологий в процессе освоения мировой художественной культуры
Аттестационная работа. Место информационно-коммуникативных технологий в процессе освоения мировой художественной культуры Техника построения эллипсов во фронтальной плоскости проекций
Техника построения эллипсов во фронтальной плоскости проекций Отечественная школа нуждается в смещении акцентов со знаниевого на компетентност- ный подход в образовании.
Отечественная школа нуждается в смещении акцентов со знаниевого на компетентност- ный подход в образовании. Презентация Сущность функционального подхода к управлению таможенными органами
Презентация Сущность функционального подхода к управлению таможенными органами  Основы индустриальной технологии строительного производства
Основы индустриальной технологии строительного производства Еңбек құқығы
Еңбек құқығы Культура древнего Китая
Культура древнего Китая JavaScript Основы программирования, часть 3
JavaScript Основы программирования, часть 3 Совершенствование пункта пропуска
Совершенствование пункта пропуска  Проект «ветеран» Выполнили: обучающиеся 9 класса Волокитина Татьяна, Шаева Наталья, Курманбаев Дуйшон Руководители: Черк
Проект «ветеран» Выполнили: обучающиеся 9 класса Волокитина Татьяна, Шаева Наталья, Курманбаев Дуйшон Руководители: Черк Посреднические договоры
Посреднические договоры 9 муз Работу сделал: Попов Митя
9 муз Работу сделал: Попов Митя Первая медицинская помощь при кровотечении РАЗРАБОТАЛ КОЖИН М.Г. 2011 г.
Первая медицинская помощь при кровотечении РАЗРАБОТАЛ КОЖИН М.Г. 2011 г. Технологические и художественные особенности изготовления нагрудного украшения "Танец стерхов"
Технологические и художественные особенности изготовления нагрудного украшения "Танец стерхов"