Содержание
- 2. Структура дисциплины Осенний семестр 2+4 часа лекций 4+4 часа лабораторных работ Зачет Весенний семестр 2+4 часа
- 3. Минимальные требования для получения зачета в осеннем семестре Сдать и защитить контрольную работу (КР защищается индивидуально
- 4. Перечень вопросов, выносимых на зачет Типы сигналов. Связь между сигналами различных типов. Задачи анализа и синтеза
- 5. ЧТО ТАКОЕ СИГНАЛ? ВОЗМОЖНЫЕ ВАРИАНТЫ КЛАССИФИКАЦИИ СИГНАЛОВ ПРОБЛЕМА ВЫБОРКИ ТЕОРЕМА КОТЕЛЬНИКОВА Вводная информация по курсу
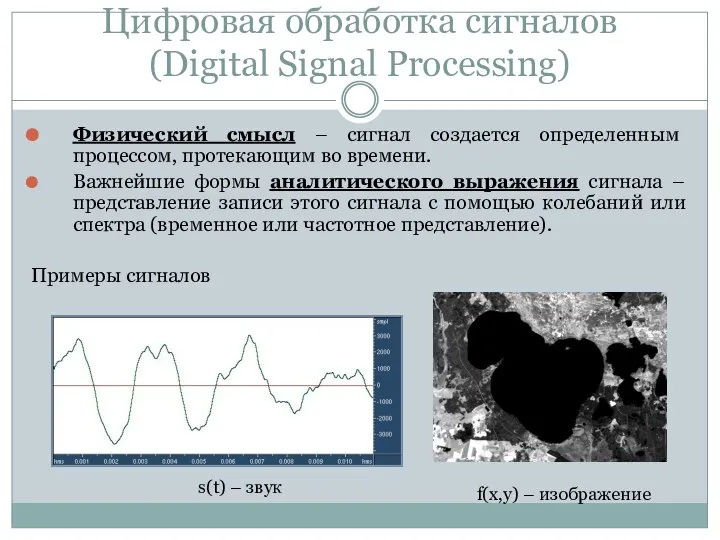
- 6. Физический смысл – сигнал создается определенным процессом, протекающим во времени. Важнейшие формы аналитического выражения сигнала –
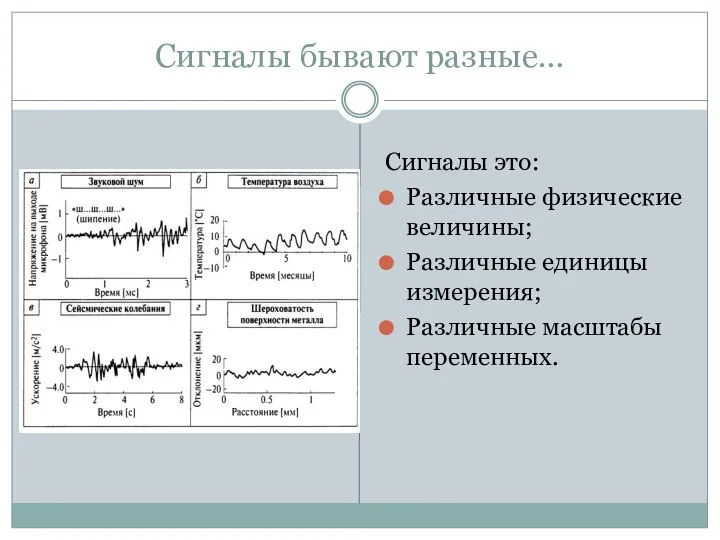
- 7. Сигналы бывают разные… Сигналы это: Различные физические величины; Различные единицы измерения; Различные масштабы переменных.
- 8. Классификация сигналов Случайный сигнал – значение такого сигнала в любой момент времени является случайной величиной. Детерминированный
- 9. Аналоговые (непрерывные) Примеры: звук в воздухе или в проводе, идущем от микрофона изображение (до ввода в
- 10. Классификация колебаний КОЛЕБАНИЯ: Каузальное колебание, имеющее начало во времени, которое можно рассматривать как причинное. Периодическое колебание,
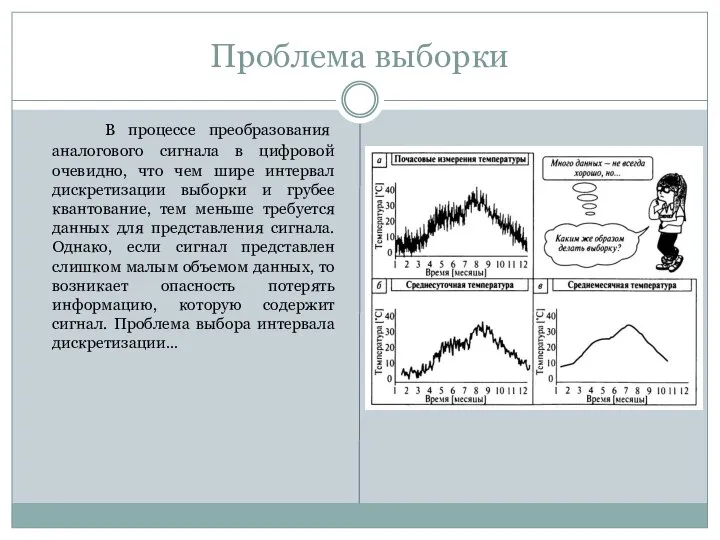
- 11. Проблема выборки В процессе преобразования аналогового сигнала в цифровой очевидно, что чем шире интервал дискретизации выборки
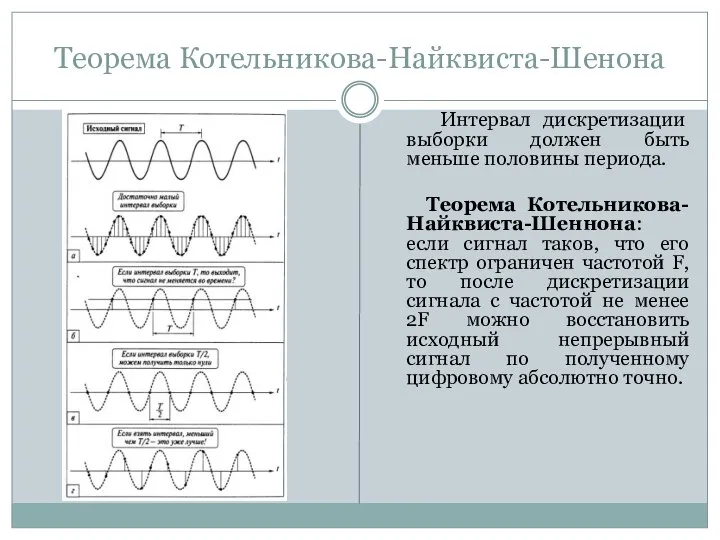
- 12. Теорема Котельникова-Найквиста-Шенона Интервал дискретизации выборки должен быть меньше половины периода. Теорема Котельникова-Найквиста-Шеннона: если сигнал таков, что
- 13. НЕОБХОДИМЫЕ МАТЕМАТИЧЕСКИЕ ПРЕДСТАВЛЕНИЯ РАЗЛОЖЕНИЕ ФУНКЦИИ В РЯД ФУРЬЕ НЕПРЕРЫВНОЕ ПРЕОБРАЗОВАНИЕ ФУРЬЕ ДИСКРЕТНОЕ ПРЕОБРАЗОВАНИЕ ФУРЬЕ Разложение в
- 14. А вот и он☺ Jean Baptiste Joseph Fourier
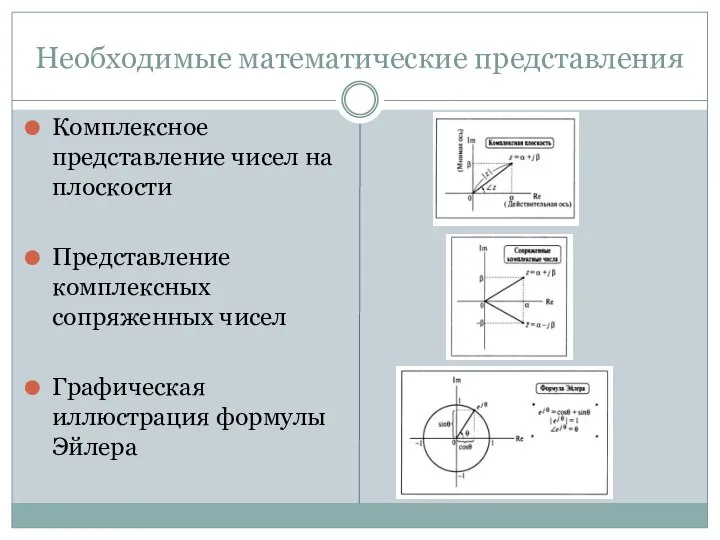
- 15. Необходимые математические представления Комплексное представление чисел на плоскости Представление комплексных сопряженных чисел Графическая иллюстрация формулы Эйлера
- 16. Необходимые математические представления Абсолютная величина (модуль) числа Аргумент числа
- 17. Ортогональные функции Множество непрерывных функций действительного переменного называется ортогональным на интервале , если При множество {Un(t)}
- 18. Впервые в 1807 году французский математик и физик Жан Батист Жозеф Фурье показал, что любую произвольную
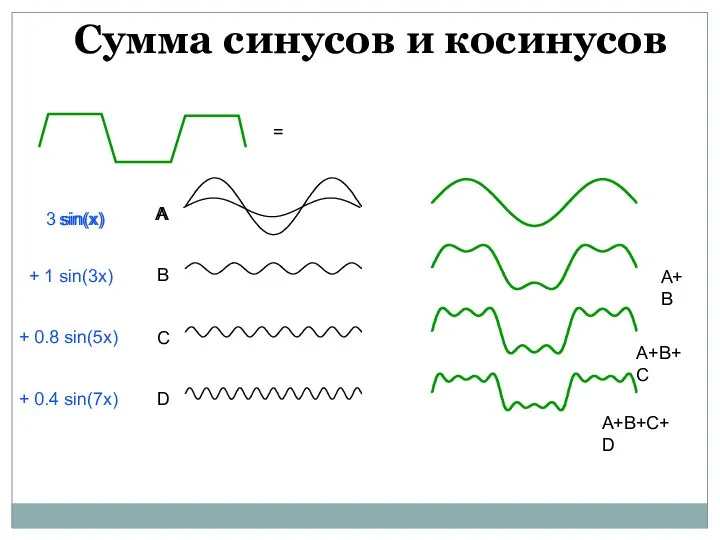
- 19. = Сумма синусов и косинусов
- 20. Прямое и обратное преобразования Фурье x(t) – исходная функция времени Прямое преобразование Фурье (отображение исходной функции
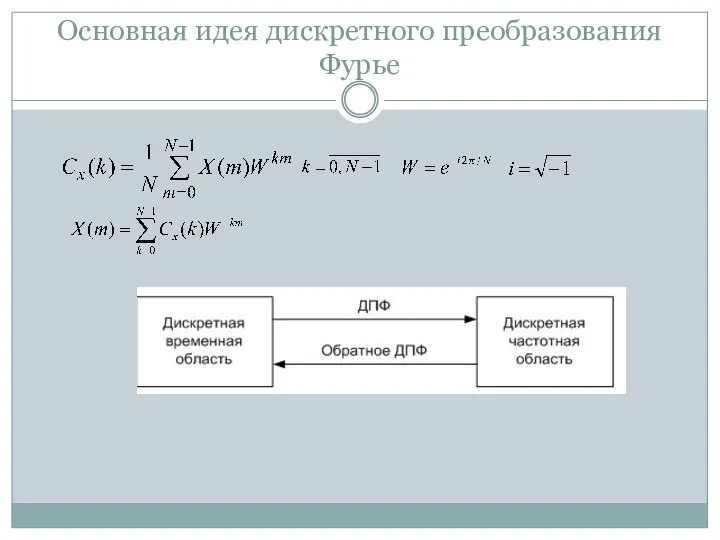
- 21. Основная идея дискретного преобразования Фурье
- 22. БПФ С ПРОРЕЖИВАНИЕМ ПО ВРЕМЕНИ БПФ С ПРОРЕЖИВАНИЕМ ПО ЧАСТОТЕ Алгоритм быстрого преобразования Фурье
- 23. Дискретное преобразование Фурье (ДПФ) Вычислительная сложность: Каждый коэффициент ДПФ требует: N комплексных умножений N-1 комплексных сложений
- 24. 8-точечное ДПФ (N=8)
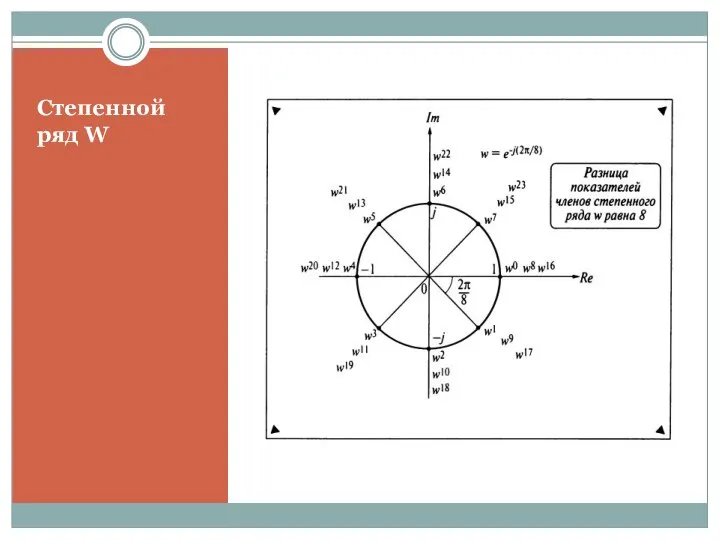
- 25. Степенной ряд W
- 26. Алгоритм БПФ с прореживанием по времени Применяются свойства симметрии и периодичности Рассматривается для случаев, когда Разделим
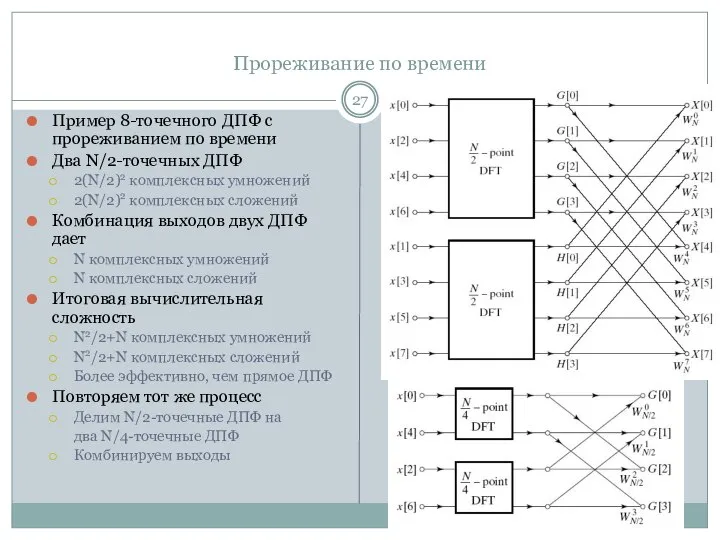
- 27. Прореживание по времени Пример 8-точечного ДПФ с прореживанием по времени Два N/2-точечных ДПФ 2(N/2)2 комплексных умножений
- 28. Прореживание по времени После двух шагов прореживания по времени Повторять пока не останутся 2-точечные ДПФ
- 29. Алгоритм БПФ С прореживанием по времени Финальная граф-схема алгоритма для N=8 Вычислительная сложность: Nlog2N комплексных сложений
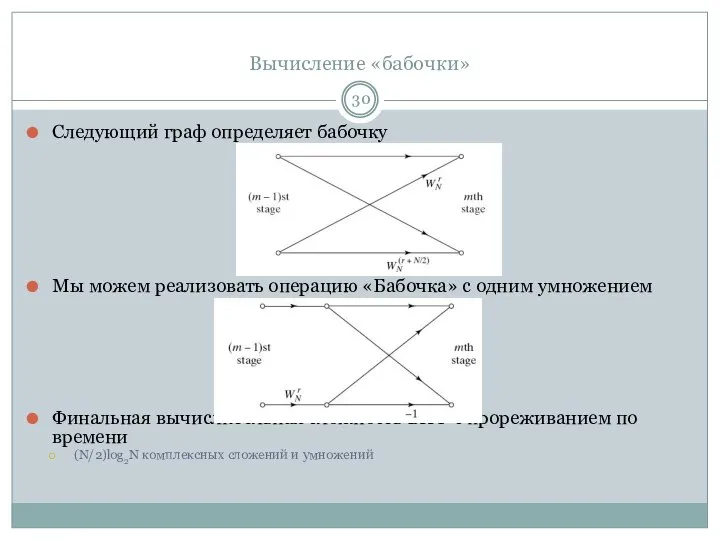
- 30. Вычисление «бабочки» Следующий граф определяет бабочку Мы можем реализовать операцию «Бабочка» с одним умножением Финальная вычислительная
- 31. Примечание к алгоритму Отметим последовательность входных элементов Бит-реверсная индексация
- 32. Примечание к алгоритму
- 33. Алгоритм БПФ с прореживанием по частоте ДПФ Разделим ДПФ на две части («верхняя» и «нижняя») Получим
- 34. Алгоритм БПФ с прореживанием по частоте Финальная граф-схема алгоритма для N=8
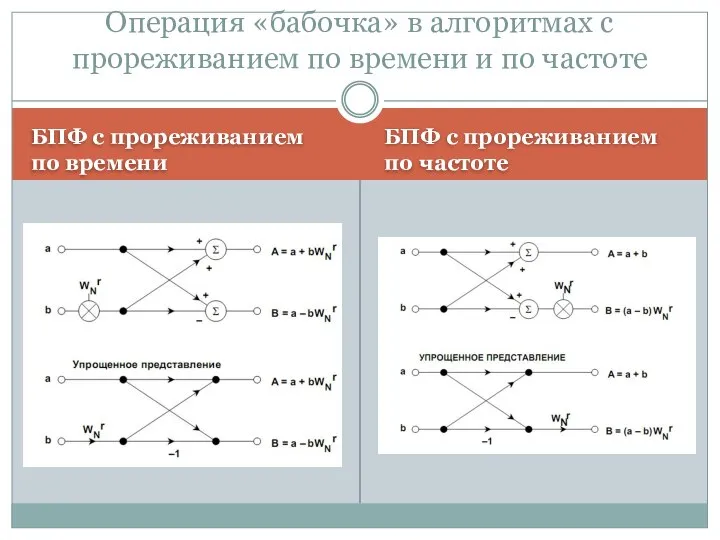
- 35. БПФ с прореживанием по времени БПФ с прореживанием по частоте Операция «бабочка» в алгоритмах с прореживанием
- 36. Практическое применение
- 37. Спектральный анализ Отображение спектров изображений Спектр – это картинка, показывающая зависимость амплитуды от частоты и от
- 38. Спектральный анализ Примеры изображений и их спектров Видно, что спектр одной синусоиды – это точка (не
- 39. Спектральный анализ Примеры изображений и их спектров По спектру прослеживаются преобладающие направления в исходной картинке Много
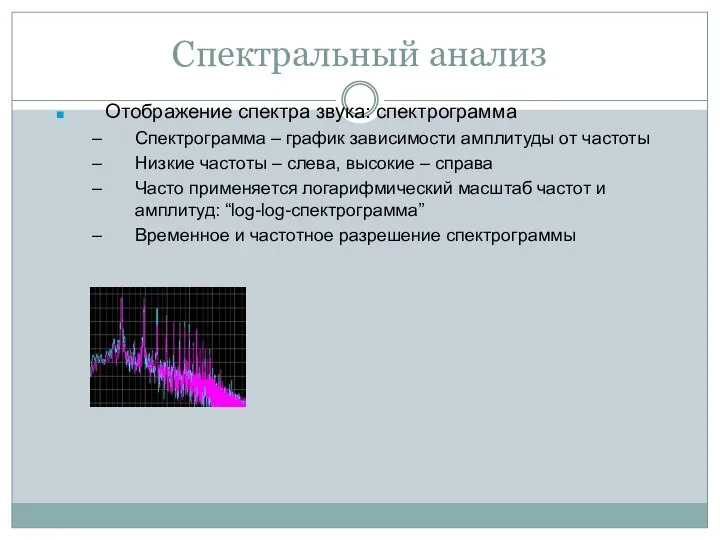
- 40. Спектральный анализ Отображение спектра звука: спектрограмма Спектрограмма – график зависимости амплитуды от частоты Низкие частоты –
- 41. Двумерное ДПФ, пример
- 42. Двумерное ДПФ, пример
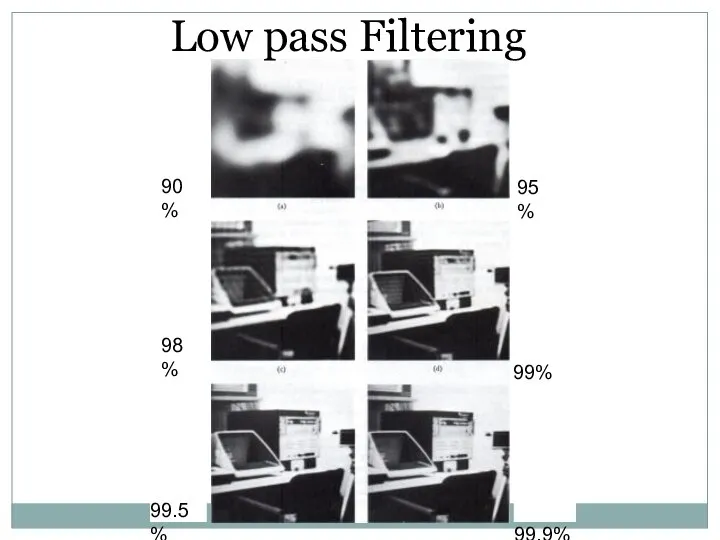
- 43. Frequency Bands Percentage of image power enclosed in circles (small to large) : 90%, 95%, 98%,
- 44. Low pass Filtering 90% 95% 98% 99% 99.5% 99.9%
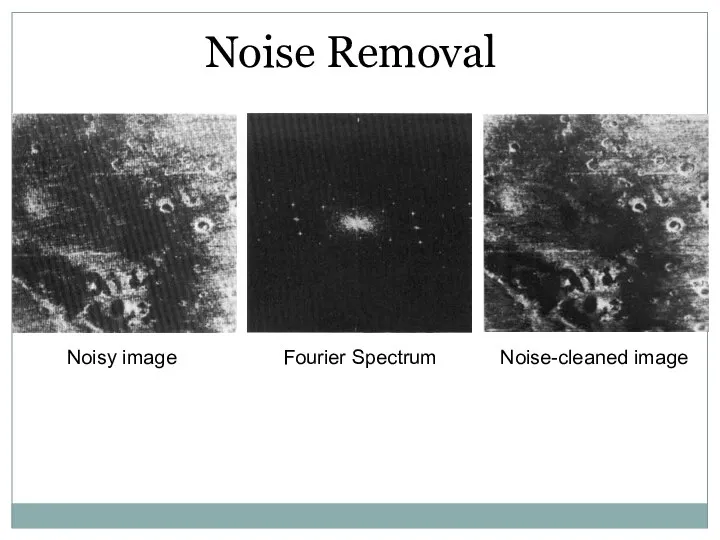
- 45. Noise Removal Noisy image
- 46. Noise Removal Noisy image Fourier Spectrum Noise-cleaned image
- 47. High Pass Filtering Original High Pass Filtered
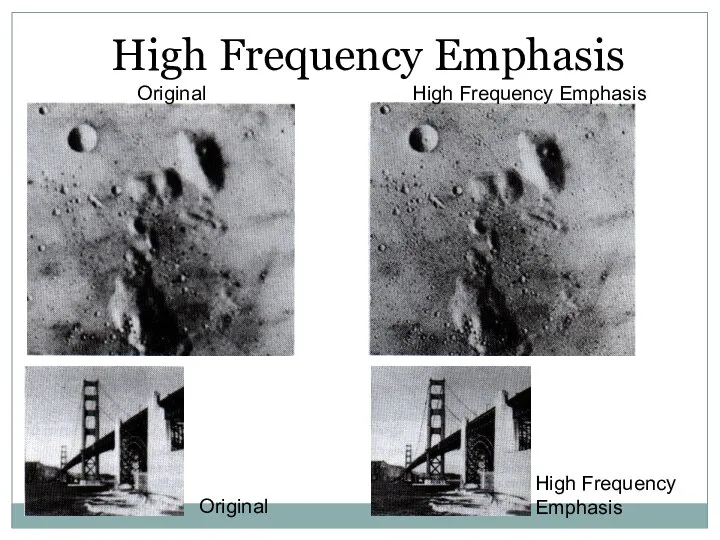
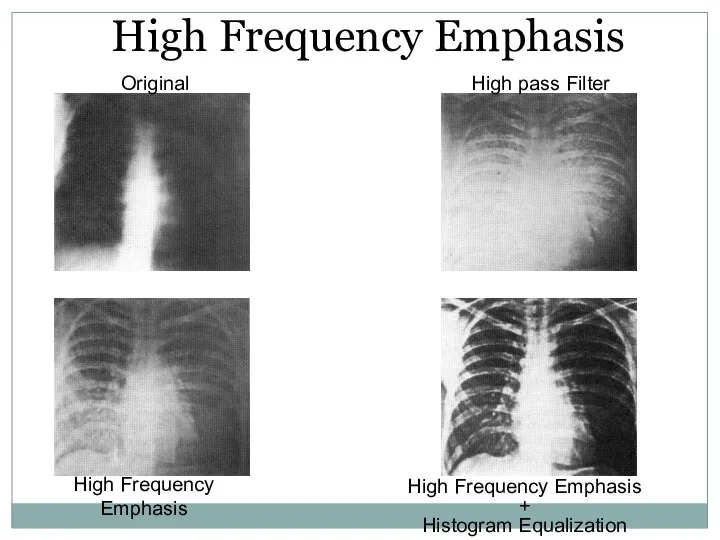
- 48. High Frequency Emphasis + Original High Pass Filtered
- 49. High Frequency Emphasis Original High Frequency Emphasis Original High Frequency Emphasis
- 50. Original High Frequency Emphasis
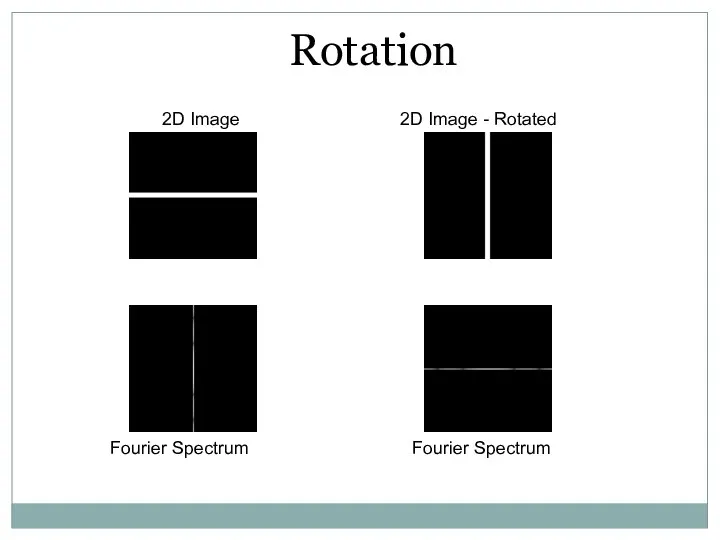
- 51. 2D Image Rotation
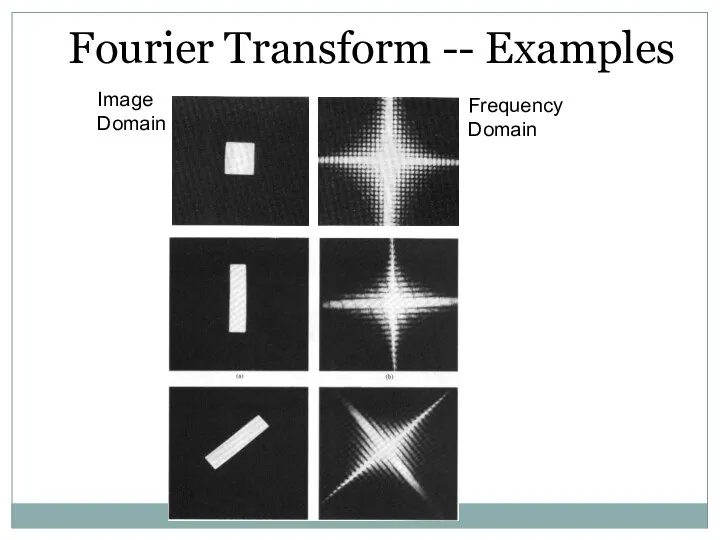
- 52. Image Domain Frequency Domain Fourier Transform -- Examples
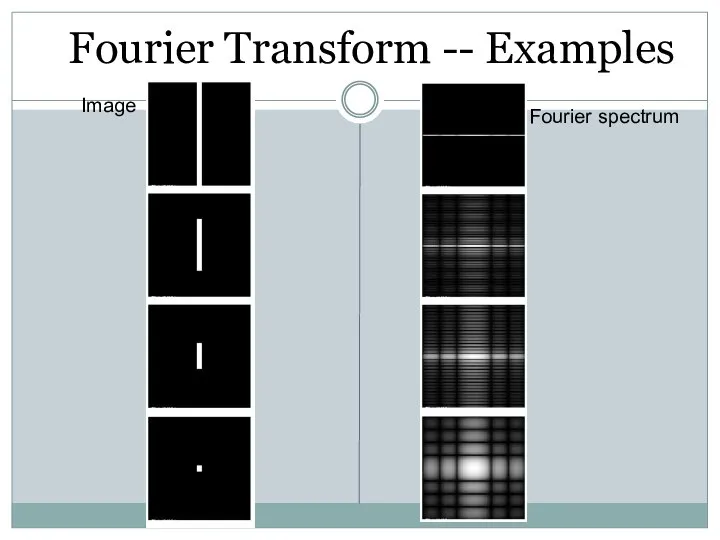
- 53. Image Fourier spectrum Fourier Transform -- Examples
- 55. Скачать презентацию

































 Этика и этикет
Этика и этикет ВАЛЕНТИН АЛЕКСАНДРОВИЧ СЕРОВ (1865-1911)
ВАЛЕНТИН АЛЕКСАНДРОВИЧ СЕРОВ (1865-1911) Презентация Социологическая концепция Т. Парсонса
Презентация Социологическая концепция Т. Парсонса Традиционная русская одежда
Традиционная русская одежда Инфаркт Миокарда
Инфаркт Миокарда Душа цветов
Душа цветов Схема управления автоматизированным электроприводом вентилятора
Схема управления автоматизированным электроприводом вентилятора Политические элиты
Политические элиты Генные болезни человека
Генные болезни человека  Проект по литературе сказы п.п.Бажова иллюстрации художников
Проект по литературе сказы п.п.Бажова иллюстрации художников  Быстрее, выше, скандальнее: когда началась гонка за допинг
Быстрее, выше, скандальнее: когда началась гонка за допинг Религиозная карта мира
Религиозная карта мира Экологические основы паразитизма в типе Круглые черви. Полная
Экологические основы паразитизма в типе Круглые черви. Полная Декоративные растения в интерьере
Декоративные растения в интерьере Презентация на тему "РЕВМАТОИДНЫЙ АРТРИТ" - скачать презентации по Медицине
Презентация на тему "РЕВМАТОИДНЫЙ АРТРИТ" - скачать презентации по Медицине Пожарно-прикладной спорт
Пожарно-прикладной спорт Визуальный инструмент разработки автоматических спецпрограмм проверки РЗА, ООО «НПП «Динамика»
Визуальный инструмент разработки автоматических спецпрограмм проверки РЗА, ООО «НПП «Динамика» Урок №31 (112) Тест «Единицы длины»
Урок №31 (112) Тест «Единицы длины»  презентация Кочкина К.А. (1) (1)
презентация Кочкина К.А. (1) (1) Обучение спортивных судей по автомобильному спорту 3 категории
Обучение спортивных судей по автомобильному спорту 3 категории Веселые бродяги - часть 2 - презентация для начальной школы
Веселые бродяги - часть 2 - презентация для начальной школы Презентация Производство по уголовным делам, рассматриваемых судом с участием присяжных заседателей
Презентация Производство по уголовным делам, рассматриваемых судом с участием присяжных заседателей Ландшафтный дизайн. Водный режим почв, дренажная система. (Лекция 2)
Ландшафтный дизайн. Водный режим почв, дренажная система. (Лекция 2) Мальчики принесли сухих веток.
Мальчики принесли сухих веток. Принципы Надлежащей производственной практики (GMP)
Принципы Надлежащей производственной практики (GMP)  Зимний праздник Святки в Витославицах
Зимний праздник Святки в Витославицах Методы монте карло
Методы монте карло Устойчивость объектов
Устойчивость объектов