Содержание
- 2. Введение Лекции 20 час + лабораторные 16 час => Экзамен Планируется 4 лаб работ Студент может
- 3. 1. Сигналы в метрическом пространстве Под сигналом обычно понимают величину, отражающую состояние физической системы. Сигналы рассматриваются
- 4. 1. Сигналы в метрическом пространстве Мы, в основном, будем рассматривать дискретные сигналы, заданные на конечном промежутке
- 5. 1. Сигналы в метрическом пространстве Мы, в основном, будем рассматривать дискретные сигналы, заданные на конечном промежутке
- 6. 1. Сигналы в метрическом пространстве Мы, в основном, будем рассматривать дискретные сигналы, заданные на конечном промежутке
- 7. Тогда энергия (работа) сигнала x(t) на интервале времени [t1,t2] будет равна Энергия (работа) дискретного сигнала, которую
- 8. Введение метрики на сигналах. Для вещественных чисел, для точек в пространстве и для векторов известна мера
- 9. (Существуют другие определения нормы, неевклидовы). Расстояние r между векторами определяется как норма их разности: B Норма
- 10. Пусть сигнал x(t) задан на интервале Нормой сигнала x(t) называется вещественное число (при условии, что интеграл
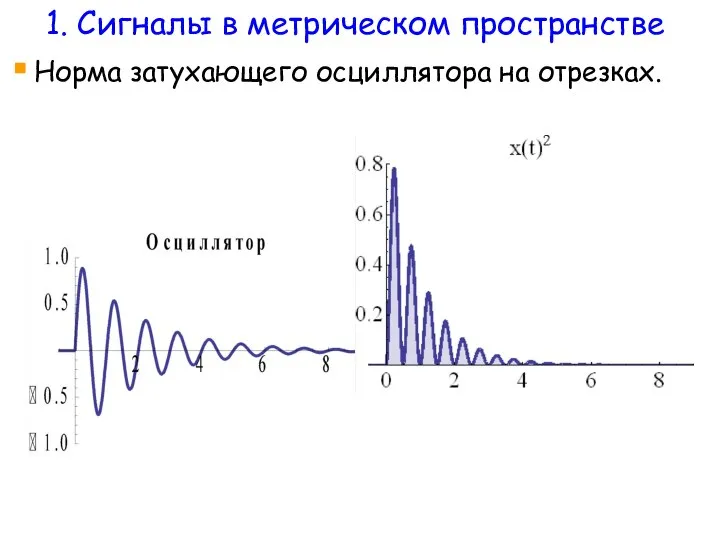
- 11. Норма затухающего осциллятора на отрезках. 1. Сигналы в метрическом пространстве
- 12. Норма затухающего осциллятора. Соответствующие интегралы 1. Сигналы в метрическом пространстве
- 13. Page То есть, на отрезке сигнал практически равен нулю (но конкретный вывод зависит от поставленной задачи!).
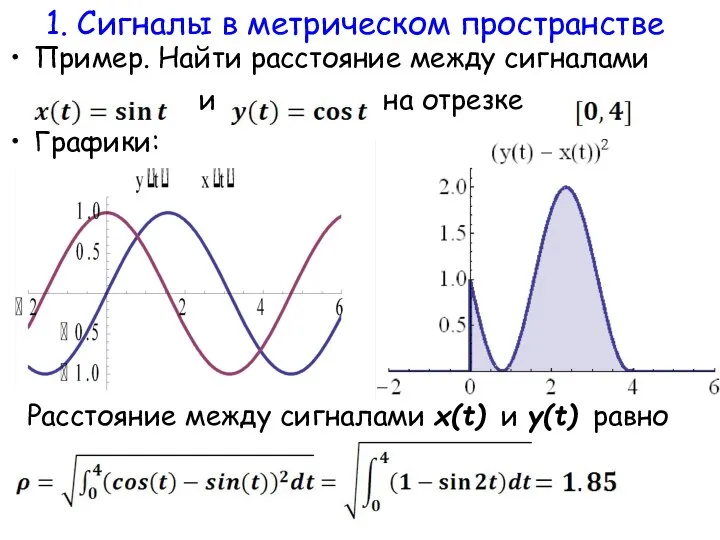
- 14. Пример. Найти расстояние между сигналами и на отрезке . Графики: Расстояние между сигналами x(t) и y(t)
- 15. Аналогично нормой дискретного сигнала x(i) называется вещественное число Расстояние между дискретными сигналами x(i) и y(i) 1.
- 16. Наряду с нормой (*) существуют и другие определения нормы, например, Мы будем использовать только норму (*).
- 17. Page Теперь рассмотрим два сигнал x(t) и y(t), заданных на промежутке времени . Скалярным произведением сигналов
- 18. Понятно, что рассматриваемый определенный интеграл должен существовать. Весовой функцией s(t) может слу-жить функция с некоторыми специальными
- 19. Норма комплекснозначного сигнала x(t) – это корень квадратный из скалярного произведения с сопряженным сигналом Сигналы x(t)
- 20. Пример. Проверить ортогональность сигналов с весовой функцией s(t) = 1 на отрезке t ϵ [-T/2,T/2] T=2π/ω,
- 21. При n ≠ m При n = m 1. Сигналы в метрическом пространстве
- 22. Сигнал x(t) не обязательно зависит от времени, аргумент t может быть любой природы. Можно обобщить понятие
- 23. Для объяснения и обоснования понятий и результатов теории сигналов необходимо элементарное знание математики. Тригонометрические функции. В
- 24. Функция sin(t) имеет период T = 2π, если аргумент t - это время, выраженное в секундах,
- 25. В математическом анализе выводится формула Эйлера, выражающая функции sin(t) и cos(t) через комплексные числа. Формула Эйлера
- 26. В дальнейшем нам понадобится выражение для суммы в комплексной форме 1. Сигналы в метрическом пространстве
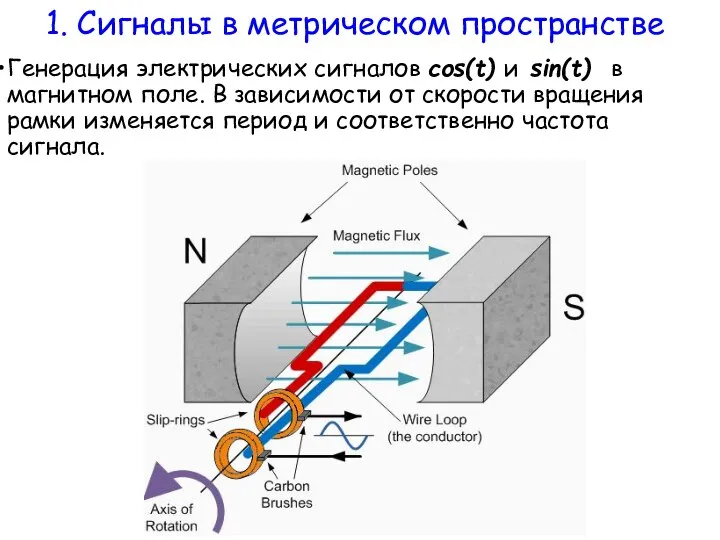
- 27. Понятие спектра сигнала. Электрический сигнал sin(t) для передачи по проводам можно получить, равномерно вращая металлическую рамку
- 28. Генерация электрических сигналов cos(t) и sin(t) в магнитном поле. В зависимости от скорости вращения рамки изменяется
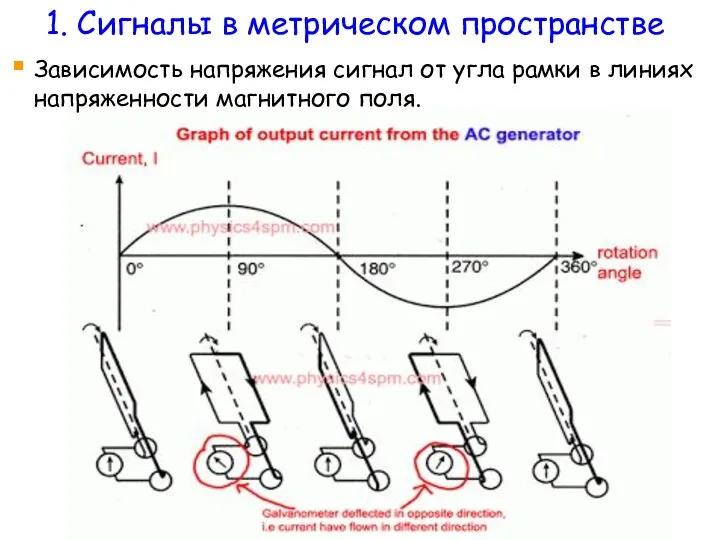
- 29. Зависимость напряжения сигнал от угла рамки в линиях напряженности магнитного поля. 1. Сигналы в метрическом пространстве
- 30. Понятие спектра сигнала. Электрический сигнал sin(t) для передачи по проводам можно получить, равномерно вращая металлическую рамку
- 31. Разумно предположить, что любой сигнал с некоторой погрешностью можно разложить в сумму функций sin(.) и cos(.)
- 32. Ортогональность функций. Система линейно независимых функций {f0(t), f1(t), ..., fk(t), ...}, заданных на некотором отрезке [a,
- 33. Функции Хаара. В 1909 г Альфред Хаар предложил систему кусочно-постоянных функций, которая стала широко применяться с
- 34. Первые 8 функций Хаара 2. Ортогональные функции
- 35. Семейство двоичных интервалов имеет важные для дальнейших построений свойства. Взаимное положение интервалов. Пусть j0, k0, j1,
- 36. Если интервал Ij+1, k0 входит в интервал Ij, k , то либо k0=2k (левая половина интервал
- 37. Если интервал Ij+1, k0 входит в интервал Ij, k , то либо k0=2k (левая половина интервал
- 38. Теперь определим вспомогательную функцию Функции pj,k(t) называются весовыми функциями Хаара. Тогда очевидно, что 2. Ортогональные функции
- 39. Функции Хаара, которые являются целью построения, получаются делением интервала-носителя функций pj,k() на две равные части, левую
- 40. Множество функций Хаара {h(t), hj,k() }, где j, k – пробе-гают все неотрицательные целые числа, называется
- 41. Случаи b) и c) - это когда один носитель входит в левую или правую половину другого,
- 42. Ортогональное разложение. Одной из основных задач для ортогональных функций является задача разложения заданной функции в ряд
- 43. Для того, чтобы найти Ak0 для конкретного k0, умножим обе части равенства на Pk0(t) и на
- 44. Ввиду ортогональности базисных функций Pk(t) все интегралы в правой части, кроме слагаемого с индексом k0, обращаются
- 45. Записывая для простоты результат с индексом k, получаем формулу Так получаются и формулы разложения в ряд
- 46. Page Исходная составляющая один период на кольце (время, за которое тепло проходит полный круг), была названа
- 47. Page 2. Ортогональные функции В основе ряда Фурье лежат тригонометрические ортогональные функции. Это базисные функции ряда
- 48. 2. Ортогональные функции Проверим ортогональность сигналов с весовой функцией s(t) = 1 на отрезке t €
- 49. 2. Ортогональные функции Если m ≠ n (при интегрировании нужно будет делить на m - n),
- 50. Page 2. Ортогональные функции То есть, для любых целых параметров m ≠ n сигналы ортогональны. При
- 51. 2. Ортогональные функции То есть, норма сигнала sin nωt равна норма сигнала cos nωt также равна
- 52. Page 2. Ортогональные функции Окончательно получаем: 1) норма сигнала sin nωt при n=1,2,… равна при n=0
- 53. 2. Ортогональные функции 3) Сигнала sin nωt и sin mωt при n≠m для всех целых n
- 54. Упражнение. Проверить ортогональность сигналов 2. Ортогональные функции
- 55. Page Коэффициенты Ak, Bk ряда Фурье вычисляются с применением свойства ортогональности базисных функций. Общий вид разложения
- 56. Так как sin0 =0, то B0 – любое число, для определенности положим его равным нулю, B0
- 57. Page Так как по результатам п 3.1. сигналы cos nωt и cos mωt при n≠m для
- 58. Page Коэффициенты Ak, Bk вычисляем аналогично, для построения Ak умножаем обе части (*) на cos kωt
- 59. Page Ввиду ортогональности все интегралы обращаются в нуль, кроме интеграла с коэффициентом Ak, и с учетом
- 60. Page Отсюда коэффициент Ak для k=1,2,… равен 3. Коэффициенты разложения в ряд Фурье коэффициент Bk вычисляем
- 61. Page 3. Коэффициенты разложения в ряд Фурье Если разложение в ряд Фурье функции x(t) записать в
- 62. Легко показать, что при разложении нечетной функции коэффициенты ряда Фурье при базисных функциях cos(·) равны нулю,
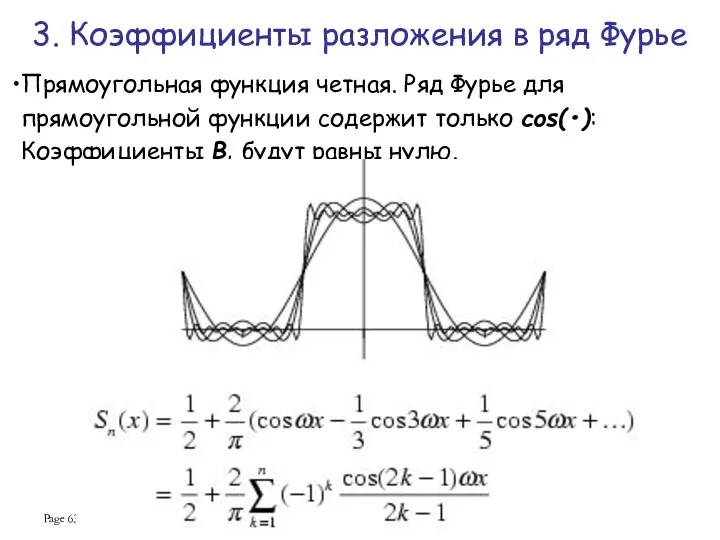
- 63. Page Прямоугольная функция четная. Ряд Фурье для прямоугольной функции содержит только cos(•): Коэффициенты Bk будут равны
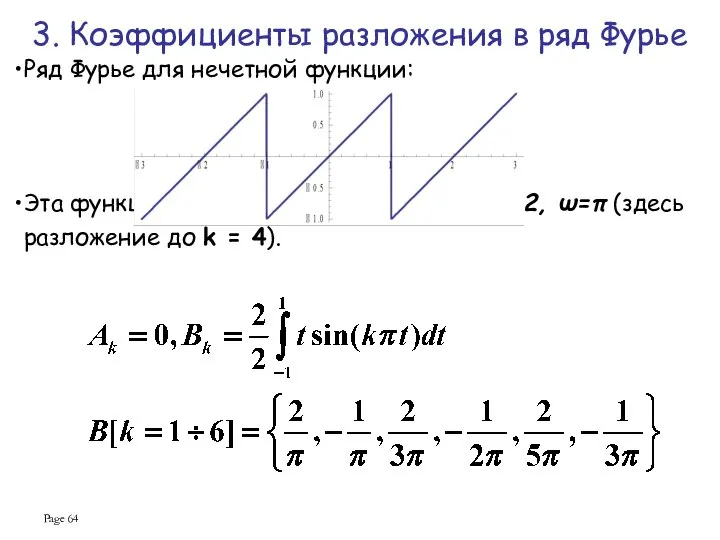
- 64. Page Ряд Фурье для нечетной функции: Эта функция разлагается в ряд синусов, T=2, ω=π (здесь разложение
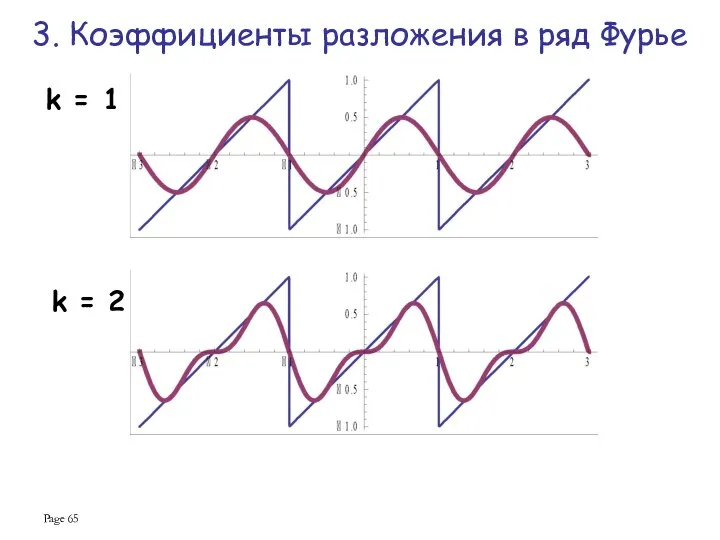
- 65. Page k = 2 k = 1 3. Коэффициенты разложения в ряд Фурье
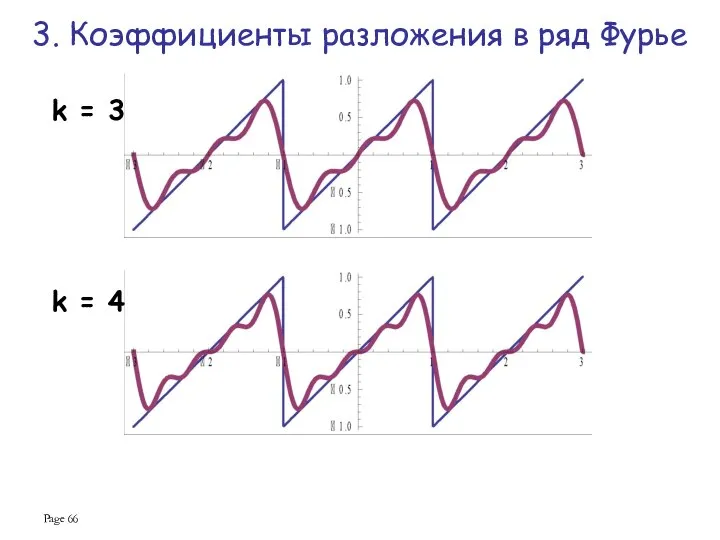
- 66. Page k = 4 k = 3 3. Коэффициенты разложения в ряд Фурье
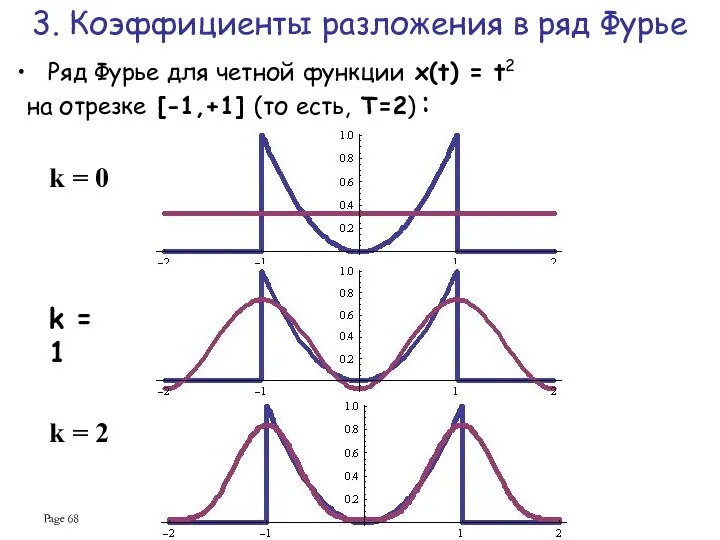
- 67. Page Разложим x(t) = t2 на отрезке [-1, 1], принимаем T=2. Функция четная, поэтому ряд содержит
- 68. Page Ряд Фурье для четной функции x(t) = t2 на отрезке [-1,+1] (то есть, Т=2) :
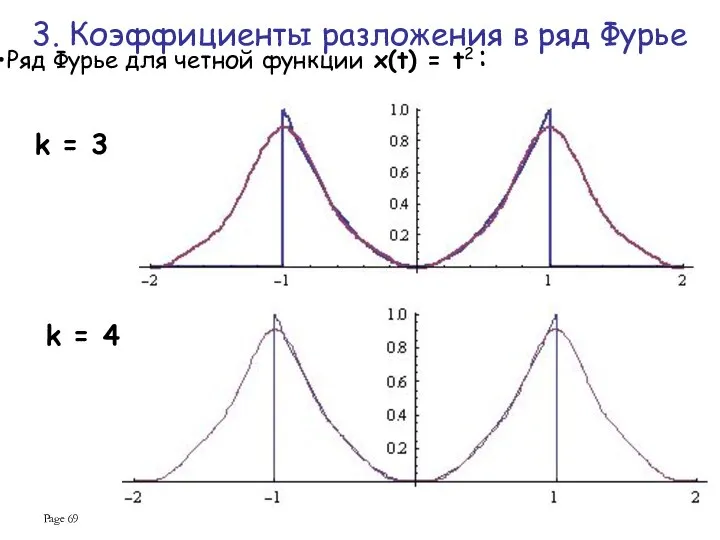
- 69. Page Ряд Фурье для четной функции x(t) = t2 : k = 3 k = 4
- 70. Следует заметить, что для некоторых функций ряд Фурье расходится, для некоторых ряд Фурье не сходится к
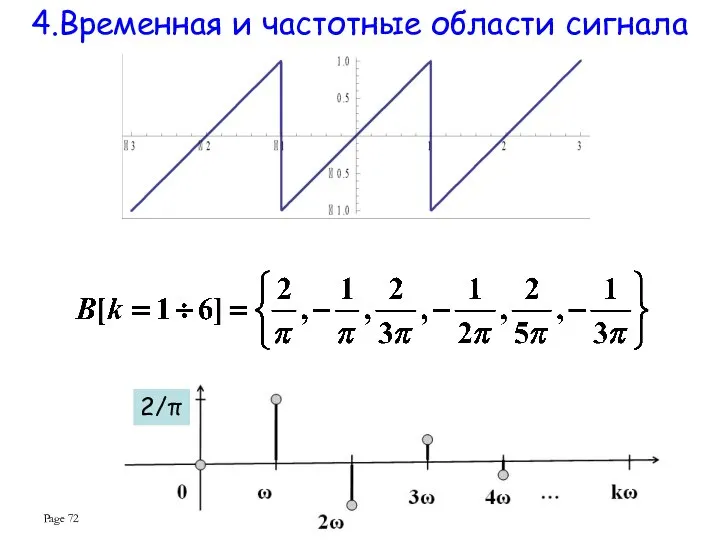
- 71. Сигнал моделируется в виде функции x(t), зависящей от времени t. Говорят, что сигнал моделируется во временной
- 72. Page 4.Временная и частотные области сигнала 2/π
- 73. Page Если увеличить период T, то частота ω уменьшится и на график коэффициентов (частотный график) изменится.
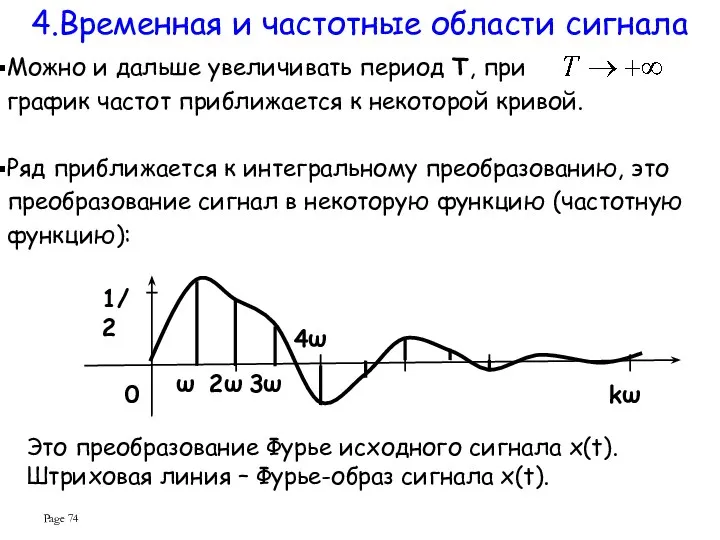
- 74. Page Можно и дальше увеличивать период T, при график частот приближается к некоторой кривой. Ряд приближается
- 75. Page Известна формула Эйлера, связывающая экспоненту с тригонометрическими функциями. 3.4. Комплексная форма ряда Фурье Заменяя sin()
- 76. Page Введем новые обозначения где Ck и C-k комплексные числа. Запишем ряд Фурье в комплексной форме:
- 78. Скачать презентацию





![Тогда энергия (работа) сигнала x(t) на интервале времени [t1,t2] будет равна](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/1473695/slide-6.jpg)



















































![Page Разложим x(t) = t2 на отрезке [-1, 1], принимаем T=2.](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/1473695/slide-66.jpg)





 Заңды жауапкершілік ұғымы, түрлері, қағидалары
Заңды жауапкершілік ұғымы, түрлері, қағидалары Адаптация и здоровье
Адаптация и здоровье 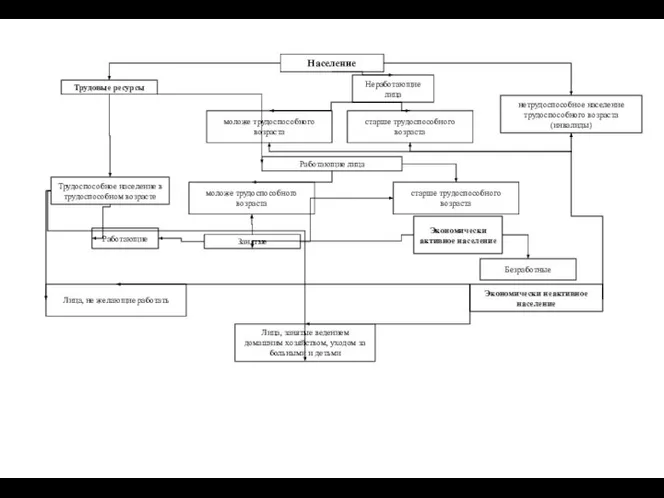 Трудовые ресурсы
Трудовые ресурсы Виды и характер деятельности человека на производстве
Виды и характер деятельности человека на производстве  Borland Delphi программалау ортасы
Borland Delphi программалау ортасы Реформа патріарха Нікона. Церковний розкол
Реформа патріарха Нікона. Церковний розкол Обзор рынка СПГ АТ региона
Обзор рынка СПГ АТ региона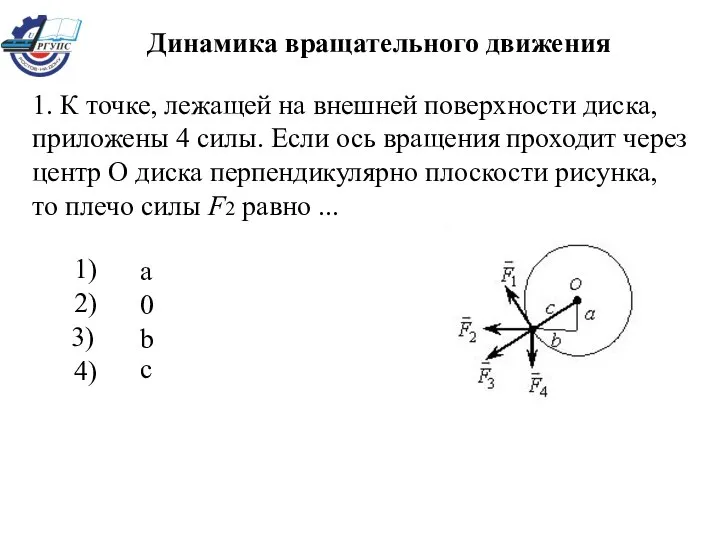 Динамика вращательного движения
Динамика вращательного движения Общая характеристика органических, включая симптоматические, психические расстройства. Психические нарушения у больных при сома
Общая характеристика органических, включая симптоматические, психические расстройства. Психические нарушения у больных при сома Инкапсуляция в классах С++
Инкапсуляция в классах С++  Решение задания повышенного уровня сложности С1 (3 балла)
Решение задания повышенного уровня сложности С1 (3 балла) Фотопрактикум
Фотопрактикум Организация комплекса просветительских мероприятий на приходе св. прав. Симеона Верхотурского
Организация комплекса просветительских мероприятий на приходе св. прав. Симеона Верхотурского Исключения. Как не допустить логических ошибок при выполнении программы (C++)
Исключения. Как не допустить логических ошибок при выполнении программы (C++) Protosoology Модификация
Protosoology Модификация Словарные слова - презентация для начальной школы
Словарные слова - презентация для начальной школы Электронная плата для self service (холодильные модули)
Электронная плата для self service (холодильные модули) Концентрация производства на предприятии
Концентрация производства на предприятии Рококо
Рококо Липиды и обмен липидов
Липиды и обмен липидов Типология конфликтов. Управление конфликтами в процессе принятия управленческих решений
Типология конфликтов. Управление конфликтами в процессе принятия управленческих решений Типи письма у сучасному світі. Чотири сім’ї алфавітів. Походження і розвиток основних алфавітів
Типи письма у сучасному світі. Чотири сім’ї алфавітів. Походження і розвиток основних алфавітів СМИ в избирательных процессах
СМИ в избирательных процессах Методы оптимизации
Методы оптимизации Религия и роль в современном мире
Религия и роль в современном мире Оказание первой медицинской помощи (часть 4 - ГУМ)
Оказание первой медицинской помощи (часть 4 - ГУМ)  Енгізудің және шығарудың құрылымдары
Енгізудің және шығарудың құрылымдары Изучение и совершенствование техники волейбола. (5-11 класс)
Изучение и совершенствование техники волейбола. (5-11 класс)