Содержание
- 2. Определение (рекурсивное) 1. Одиночная вершина есть двоичное дерево. 2. Двоичное дерево – это вершина (V), соединенная
- 3. Пример двоичного дерева Кружочками обозначены вершины дерева, стрелками - связи между вершинами.
- 4. Высота дерева (h) определяется как число вершин в самой длинной ветви дерева. Начальная вершина называется корнем.
- 5. Словарь tree [три] – дерево root [рут] – корень vertex [вётэкс] – вершина right [райт] –
- 6. Свойство 1: Максимальное число вершин в двоичном дереве высоты h равно nmax(h)= 2h – 1 Доказательство:
- 7. Свойство 2: Минимально возможная высота двоичного дерева с n вершинами равна hmin(n) = ⎡log(n+1)⎤ Доказательство: Из
- 8. Определение Двоичное дерево называют идеально сбалансированным (ИСД), если для каждой его вершины размеры левого и правого
- 9. Пример
- 10. Свойство 3: Высота ИСД с n вершинами минимальна. hисд(n) = hmin(n) = ⎡log(n+1)⎤
- 11. Каждая вершина содержит данные и указатели на вершину слева и справа. В качестве заголовка для дерева
- 12. Структура вершины дерева struct Vertex { int Data; Vertex * Left; Vertex * Right; } ;
- 13. Графическое представление
- 14. Существует много работ, которые можно выполнять с деревьями. Например, посадка, подкормка, подстрижка, полив, окучивание и т.п.
- 15. Основные операции с деревьями Определение. Обход дерева – выполнение некоторой операции с каждой его вершиной. Существуют
- 16. Обходы легко программируются с помощью рекурсивных процедур. Пример. Процедура обхода дерева сверху вниз. void Obhod1 (
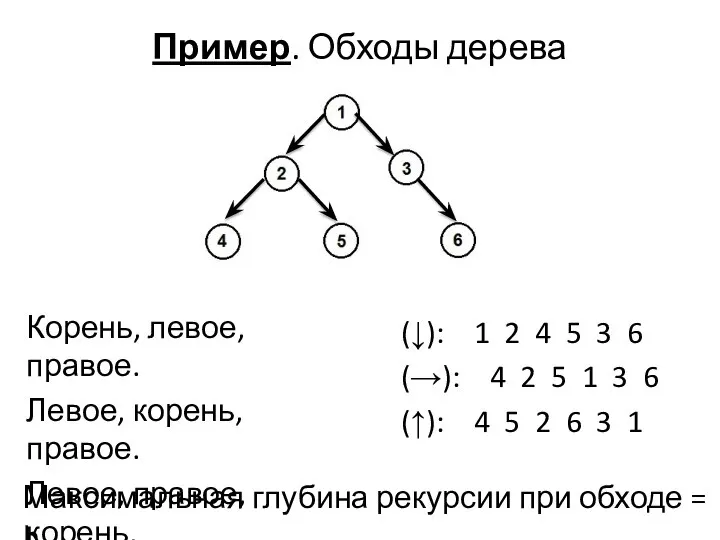
- 17. Пример. Обходы дерева Корень, левое, правое. Левое, корень, правое. Левое, правое, корень. (↓): 1 2 4
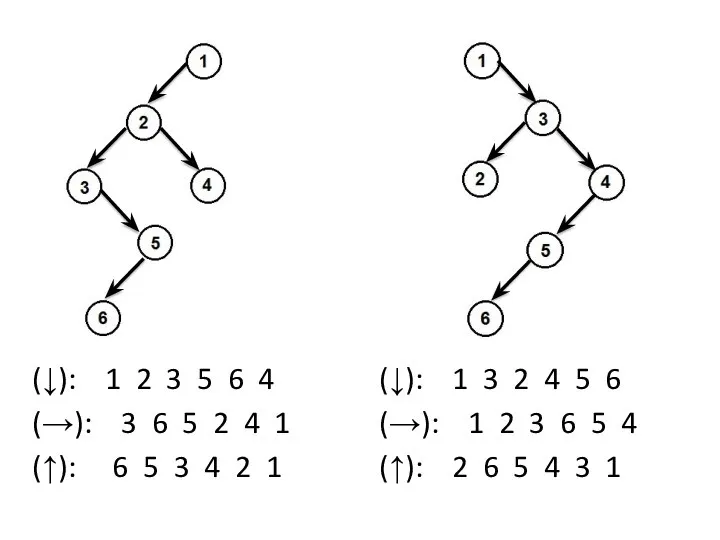
- 18. (↓): 1 3 2 4 5 6 (→): 1 2 3 6 5 4 (↑): 2
- 19. 3.9. Деревья поиска Двоичные деревья часто используются для представления данных, среди которых идет поиск элементов по
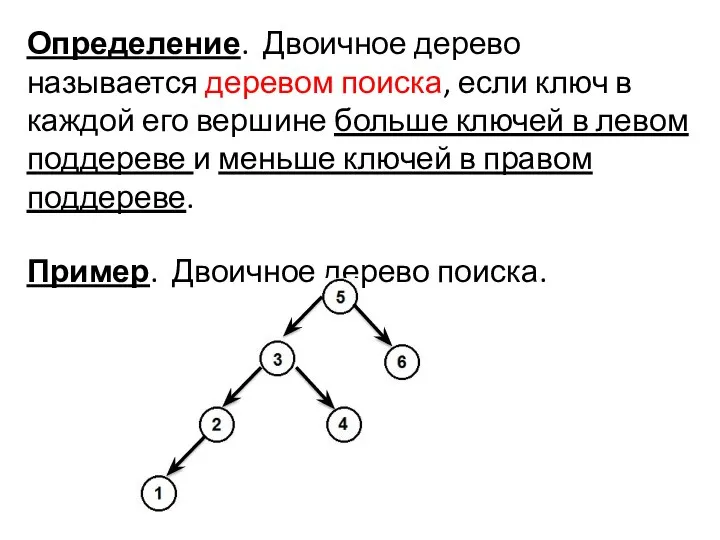
- 20. Определение. Двоичное дерево называется деревом поиска, если ключ в каждой его вершине больше ключей в левом
- 21. 3.9.1. Поиск вершины с ключом Х Начиная с корневой вершины дерева, сравниваем ключ поиска с данными
- 22. Поиск вершины с ключом Х Алгоритм на псевдокоде p := Root DO (p != NULL) IF
- 23. Трудоемкость поиска по дереву Максимальное количество сравнений при поиске: Cmax =2h Идеально сбалансированное дерево: Cmax= 2
- 24. Построение ИСДП из элементов массива А = (a1, a2 ,…, an): Отсортировать массив по возрастанию. Построить
- 25. 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15
- 26. Построение ИСДП Алгоритм на псевдокоде Vertex* ISDP (L,R) IF (L>R) return NULL; ELSE m := ⎡(L+R)/2⎤
- 27. В реальности количество элементов данных заранее неизвестно и они поступают последовательно в произвольном порядке. Требуется строить
- 28. Случайные деревья поиска. Все преимущества деревьев реализуются именно тогда, когда меняется их структура в ходе выполнения
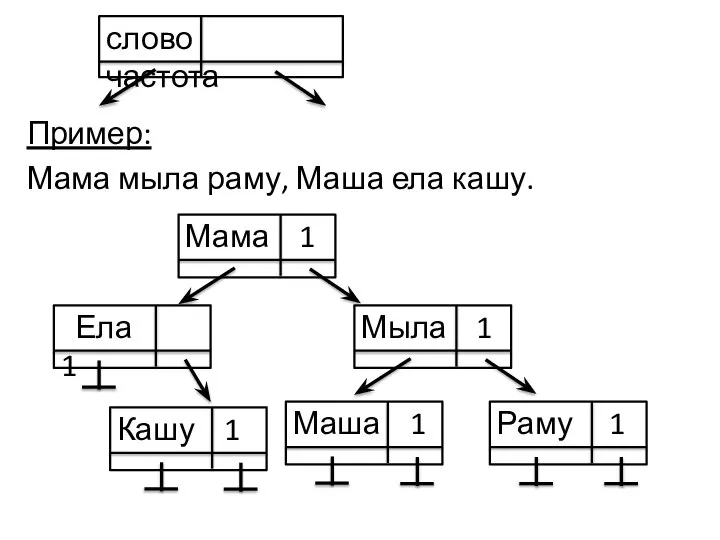
- 29. Пример: Мама мыла раму, Маша ела кашу. слово частота Мама 1 Ела 1 Мыла 1 Раму
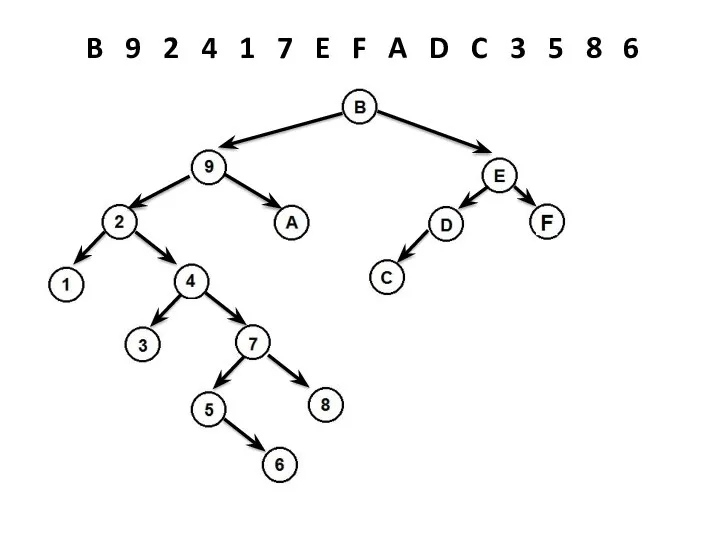
- 30. Построение СДП Идея: построение выполняется путем добавления новых вершин в дерево. Если дерево пустое, то создать
- 31. B 9 2 4 1 7 E F A D C 3 5 8 6
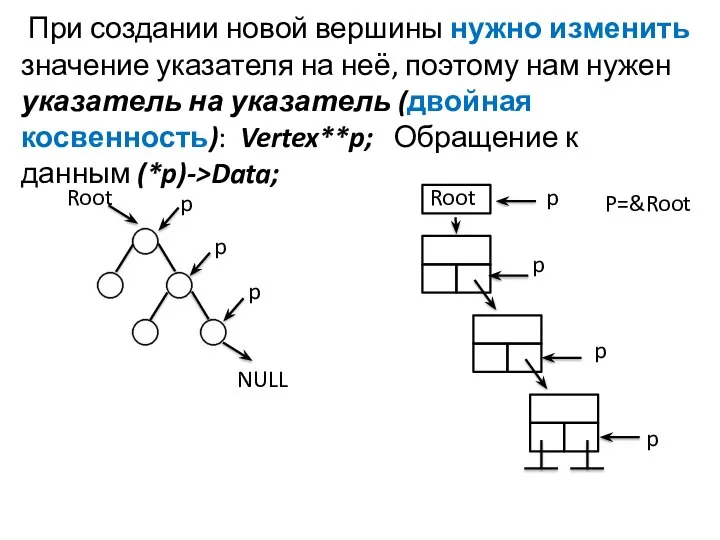
- 32. При создании новой вершины нужно изменить значение указателя на неё, поэтому нам нужен указатель на указатель
- 33. Обозначения: Root - корень, D – данные, p - указатель на указатель Добавить (данные D в
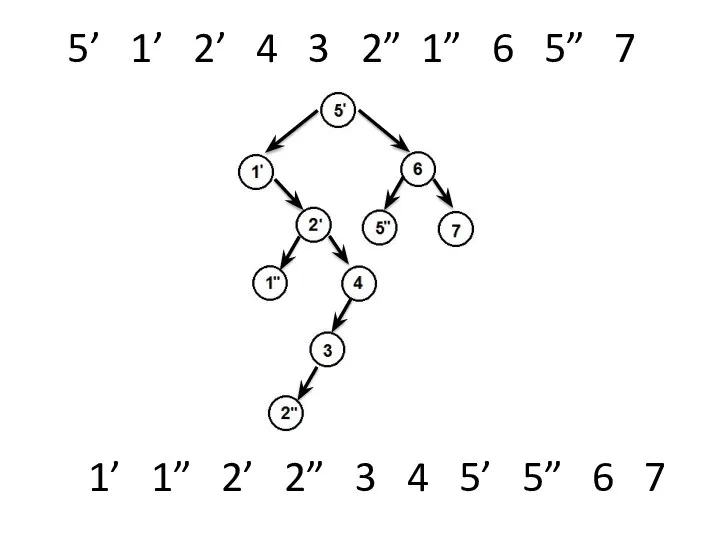
- 34. Хотя назначение этого алгоритма - поиск с включением, его можно использовать и для сортировки. Если мы
- 35. 5’ 1’ 2’ 4 3 2” 1” 6 5” 7 1’ 1” 2’ 2” 3 4
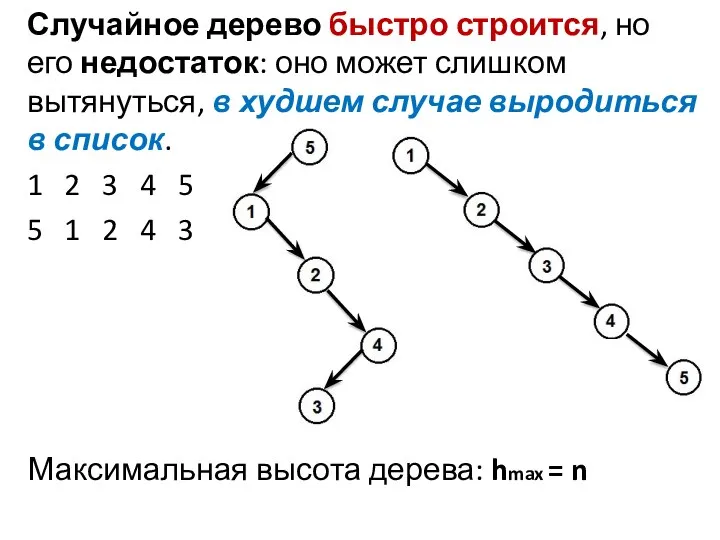
- 36. Случайное дерево быстро строится, но его недостаток: оно может слишком вытянуться, в худшем случае выродиться в
- 39. Скачать презентацию



![Словарь tree [три] – дерево root [рут] – корень vertex [вётэкс]](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/1365723/slide-4.jpg)
























 Неотложные состояния в эндокринологии
Неотложные состояния в эндокринологии  Транспортные средства. Макеты и модели
Транспортные средства. Макеты и модели  Банки на рынке ценных бумаг Инвестиционные операции банков
Банки на рынке ценных бумаг Инвестиционные операции банков  Презентация Государственный и общественный строй в Древнем Вавилоне и Ассирии
Презентация Государственный и общественный строй в Древнем Вавилоне и Ассирии  Тактирование приложений
Тактирование приложений Умный часовой
Умный часовой Счетчики с произвольным порядком счета. Лекция 5
Счетчики с произвольным порядком счета. Лекция 5 Летние учебно-тренировочные сборы в г. Уфа
Летние учебно-тренировочные сборы в г. Уфа МЕДИАТОРНЫЕ СРЕДСТВА ПЕРИФЕРИЧЕСКОГО ДЕЙСТВИЯ Н-ХОЛИНЕРГИЧЕСКИЕ СРЕДСТВА
МЕДИАТОРНЫЕ СРЕДСТВА ПЕРИФЕРИЧЕСКОГО ДЕЙСТВИЯ Н-ХОЛИНЕРГИЧЕСКИЕ СРЕДСТВА Региональная власть в системе политических сетей
Региональная власть в системе политических сетей Двигательные умения и навыки
Двигательные умения и навыки Презентация по алгебре Решение уравнений,содержащих переменную под знаком модуля
Презентация по алгебре Решение уравнений,содержащих переменную под знаком модуля  Культурное пространство России XVI века
Культурное пространство России XVI века Презентация____
Презентация____ Минералы
Минералы  ФСКН РФ Понятие, структура, полномочия.
ФСКН РФ Понятие, структура, полномочия.  Noţiunea, obiectul şi sistemul dreptului ecologic
Noţiunea, obiectul şi sistemul dreptului ecologic «ЭКСПОРТНЫЙ КОНТРОЛЬ СФУ» ОТДЕЛ ВНЕШНЕЭКОНОМИЧЕСКОЙ ДЕЯТЕЛЬНОСТИ И ТРАНСФЕРА ТЕХНОЛОГИЙ г. КРАСНОЯРСК 2008г.
«ЭКСПОРТНЫЙ КОНТРОЛЬ СФУ» ОТДЕЛ ВНЕШНЕЭКОНОМИЧЕСКОЙ ДЕЯТЕЛЬНОСТИ И ТРАНСФЕРА ТЕХНОЛОГИЙ г. КРАСНОЯРСК 2008г. Телефонный этикет
Телефонный этикет Поняття системи фізичного виховання. Лекція 2
Поняття системи фізичного виховання. Лекція 2 Фольклор Древней Руси
Фольклор Древней Руси Лек. 1. Первобытный строй_значение
Лек. 1. Первобытный строй_значение Программирование на языке Pascal
Программирование на языке Pascal ГТО в 21 веке
ГТО в 21 веке Организация и методические основы проведения урока физической культуры
Организация и методические основы проведения урока физической культуры  Слова жыцця на чэрвень
Слова жыцця на чэрвень Шаблоны функций
Шаблоны функций Технология приготовления слоеного теста
Технология приготовления слоеного теста