Содержание
- 2. Формула Тейлора для функции нескольких переменных. ТЕОРЕМА. Пусть функция z = f(x, y) имеет в окрестности
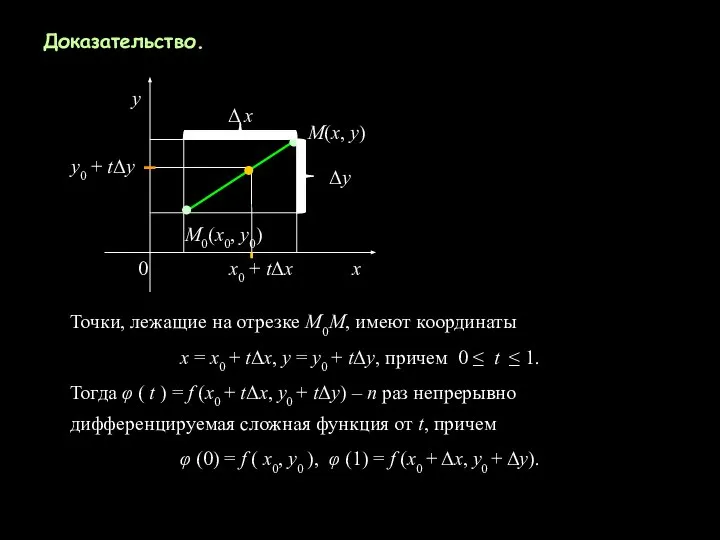
- 3. Доказательство. Точки, лежащие на отрезке М0М, имеют координаты х = х0 + tΔx, y = y0
- 4. Применяя правило нахождения производной сложной функции, получим: Аналогично По индукции получим, что
- 5. Запишем для функции φ(t) формулу Тейлора с остатком в форме Лагранжа: Полагая t = 1, получим
- 6. ЗАМЕЧАНИЕ. При соблюдении условий теоремы имеет место также формула Тейлора с остаточным членом в форме Пеано:
- 7. Локальные экстремумы функции нескольких переменных. ОПРЕДЕЛЕНИЕ. Пусть функция u = f(х1, х2, ... хm) определена в
- 8. Необходимое условие экстремума. ТЕОРЕМА. Если в точке экстремума М0 функции f(М) существует частная производная по какой-либо
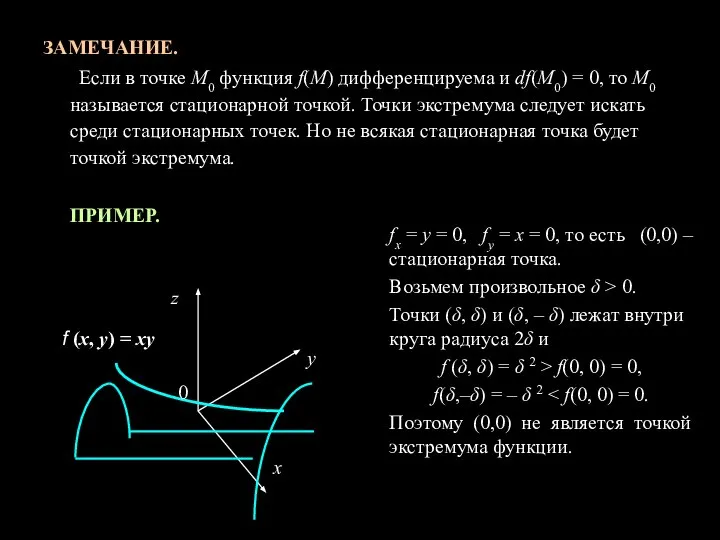
- 9. ЗАМЕЧАНИЕ. Если в точке М0 функция f(М) дифференцируема и df(М0) = 0, то М0 называется стационарной
- 10. Достаточные условия экстремума. ТЕОРЕМА. Пусть функция f(M) имеет в окрестности точки M0 непрерывные частные производные второго
- 11. Так как по условию теоремы df(х0,y0) = 0 , то полное приращение функции в критической точке
- 12. В нашем случае переменные связаны соотношением и поэтому одновременно не равны нулю. Квадратичная форма – непрерывная
- 13. СЛЕДСТВИЕ. Пусть z = f(x, y), M0(х0, у0) – стационарная точка этой функции. Исследуем второй дифференциал
- 15. ПРИМЕР. Исследовать на локальный экстремум функцию z = x3 + 3xy2 – 39x – 36y +
- 16. Ее главные миноры равны:
- 18. Скачать презентацию













 Где живут слоны? Почему слоны не живут в Воронежской области?
Где живут слоны? Почему слоны не живут в Воронежской области? Теоретические основы электротехники. Нелинейные электрические цепи
Теоретические основы электротехники. Нелинейные электрические цепи Кейс на тему «ОСАГО без страхования жизни»
Кейс на тему «ОСАГО без страхования жизни» Структура нормы права
Структура нормы права Информация как основа принятия решений в экономических задачах
Информация как основа принятия решений в экономических задачах Типы, переменные, управляющие инструкции. Ссылочные типы и переменные. (Тема 2.3)
Типы, переменные, управляющие инструкции. Ссылочные типы и переменные. (Тема 2.3) Эзофагопластика
Эзофагопластика Основные принципы торговой политики РФ
Основные принципы торговой политики РФ Использование ИКТ на уроках географии. Пирогова Наталья Анатольевна Учитель географии МБОУ СОШ №120
Использование ИКТ на уроках географии. Пирогова Наталья Анатольевна Учитель географии МБОУ СОШ №120 Религия как одна из форм культуры
Религия как одна из форм культуры БОРИС МИХАЙЛОВИЧ КУСТОДИЕВ (1878-1927)
БОРИС МИХАЙЛОВИЧ КУСТОДИЕВ (1878-1927)  Алгоритмы с ветвящейся структурой
Алгоритмы с ветвящейся структурой Электрокардиография Основные нормативы ЭКГ
Электрокардиография Основные нормативы ЭКГ Анализ причин терроризма как основной угрозы XXI века
Анализ причин терроризма как основной угрозы XXI века Я знаю свої права
Я знаю свої права Презентация на тему Закономерности изменчивости: модификационная и мутационная изменчивость
Презентация на тему Закономерности изменчивости: модификационная и мутационная изменчивость  Регуляция соматических функций
Регуляция соматических функций РУССКОЕ ИЗОБРАЗИТЕЛЬНОЕ ИСКУССТВО
РУССКОЕ ИЗОБРАЗИТЕЛЬНОЕ ИСКУССТВО Мошенничество в сфере кредитования
Мошенничество в сфере кредитования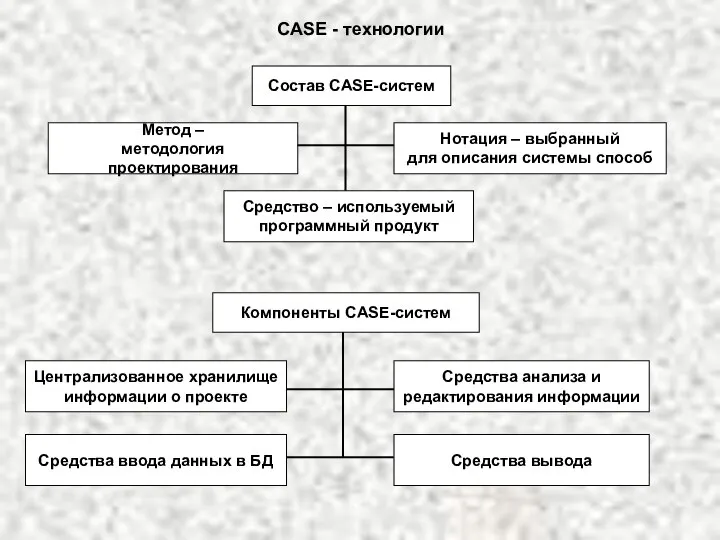 Case технология
Case технология  Т Е М А «ПРОДАЖА НЕДВИЖИМОСТИ. ПРОДАЖА ПРЕДПРИЯТИЯ»
Т Е М А «ПРОДАЖА НЕДВИЖИМОСТИ. ПРОДАЖА ПРЕДПРИЯТИЯ» Основы языка структурированных запросов SQL
Основы языка структурированных запросов SQL Понятие интерфейса пользователя
Понятие интерфейса пользователя Қазақ фонологиясының өзекті мәселелері
Қазақ фонологиясының өзекті мәселелері Презентация Правовая характеристика и особенности дисциплинарной ответственности должностных лиц таможенных органов
Презентация Правовая характеристика и особенности дисциплинарной ответственности должностных лиц таможенных органов  Новейшая геополитика России
Новейшая геополитика России Парные звонкие и глухие согласные в корне слова. 2 класс
Парные звонкие и глухие согласные в корне слова. 2 класс Основы конституционного права РФ. Тема 5
Основы конституционного права РФ. Тема 5