Содержание
- 2. Введение. Краткая историческая справка о фракталах. Фракталы – молодой раздел дискретной математики. В 1904 году швед
- 3. Фракталы – элементы геометрии в природе. Фракталы - средства для описания таких объектов как модели горных
- 4. Объекты, обладающие фрактальными свойствами, в природе. Кораллы Морские звезды и ежи Морские раковины Цветы и растения
- 5. Определение терминологии «фракталы». Фракталы - это геометрические фигуры, которые удовлетворяют одному или нескольким из следующих свойств:
- 6. Классы фракталов Фрактал – структура, состоящая из частей (субструктур), подобных целому. Часть фракталов, как элементов природы,
- 8. Процедуры получения фрактальных множеств. Это простая рекурсивная процедура получения фрактальных кривых: задают произвольную ломаную с конечным
- 9. Показано пять шагов построения ломаной Коха: отрезок единичной длины (а), делится на три части (k =
- 10. Снежинка Коха (фрактал Коха) В Качестве основы построения можно брать не отрезки единичной длины, а равносторонний
- 11. Губки Менгера. Кроме одномерных есть и трёхмерные фракталы. На рис. в трехмерном пространстве изображена губка Менгера
- 13. Скачать презентацию
Введение. Краткая историческая справка о фракталах.
Фракталы – молодой раздел дискретной математики.
В
Введение. Краткая историческая справка о фракталах.
Фракталы – молодой раздел дискретной математики.
В
В 1918 году француз Жюлиа описал целое семейство фракталов.
В 1938 году Пьер Леви опубликовал статью «Плоские и пространственные кривые и поверхности, состоящие из частей, подобных целому».
В 1982 Бенуа Мандельброта опубликовал книгу «Фрактальная геометрия природы».
С помощью простых конструкций и формул получаются изображения.
Появилась «фрактальная живопись».
С 1993 г. Из-во World Scientific издаёт журнал «Фракталы».
Фракталы – элементы геометрии в природе.
Фракталы - средства для описания таких
Фракталы – элементы геометрии в природе.
Фракталы - средства для описания таких
Или такие: лист папоротника, облака, клякса.
Изображения таких предметов можно представить с помощью фрактальной графики.
Объекты, обладающие фрактальными свойствами, в природе.
Кораллы
Морские звезды и ежи
Морские раковины
Цветы и растения (брокколи, капуста)
Плоды
Объекты, обладающие фрактальными свойствами, в природе.
Кораллы
Морские звезды и ежи
Морские раковины
Цветы и растения (брокколи, капуста)
Плоды
Кроны деревьев и листья растений
Кровеносная система и бронхи людей и животных
В неживой природе:
Границы географических объектов (стран, областей, городов)
Береговые линии
Горные хребты
Снежинки
Облака
Молнии
Образующиеся на стеклах узоры
Кристаллы
Сталактиты, сталагмиты, геликтиты.
Определение терминологии «фракталы».
Фракталы - это геометрические фигуры, которые удовлетворяют одному или
Определение терминологии «фракталы».
Фракталы - это геометрические фигуры, которые удовлетворяют одному или
Обладает сложной нетривиальной структурой при любом увеличении (на всех масштабах);
Является (приближённо) самоподобной.
Обладает дробной хаусдорфовой (фрактальной) размерностью или превосходящей топологическую;
Может быть построена рекурсивными процедурами.
Для регулярных фигур таких, как окружность, эллипс, график гладкой функции небольшой фрагмент в очень крупном масштабе похож на фрагмент прямой. Для фрактала увеличение масштаба не ведёт к упрощению структуры, для всех масштабов мы увидим одинаково сложные картины.
Классы фракталов
Фрактал – структура, состоящая из частей (субструктур), подобных целому.
Часть фракталов,
Классы фракталов
Фрактал – структура, состоящая из частей (субструктур), подобных целому.
Часть фракталов,
Остальная часть может быть отнесена к классу динамических фракталов (алгебраических).
Процедуры получения фрактальных множеств.
Это простая рекурсивная процедура получения фрактальных кривых: задают
Процедуры получения фрактальных множеств.
Это простая рекурсивная процедура получения фрактальных кривых: задают
если n = 3, k = 3, то d = 1; если n = 9, k = 3, то d = 2; если n = 27, k = 3, то d = 3.
если n = 4, k = 4, то d = 1; если n = 16, k = 4, то d = 2; если n = 64, k = 4, то d = 3. Размерность пространства выражается целыми числами: d = 1, 2, 3; для n = 64, величина d равна
Изображено: деление единичного отрезка на 3 части (а), единичной квадратной площадки на 9 частей (б), единичного куба на 27 частей (в) и на 64 части (г). Число частей n, коэффициент масштабирования — k, а размерность пространства — d. Имеем следующие соотношения: n = kd,
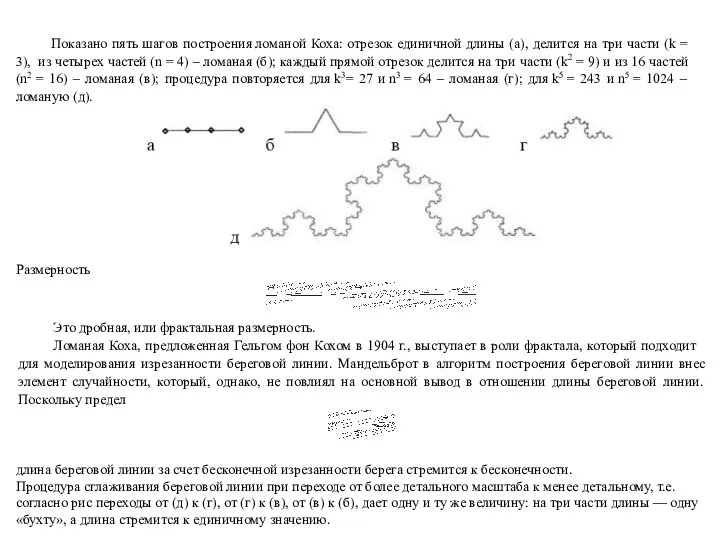
Показано пять шагов построения ломаной Коха: отрезок единичной длины (а), делится на
Показано пять шагов построения ломаной Коха: отрезок единичной длины (а), делится на
Размерность
Это дробная, или фрактальная размерность.
Ломаная Коха, предложенная Гельгом фон Кохом в 1904 г., выступает в роли фрактала, который подходит для моделирования изрезанности береговой линии. Мандельброт в алгоритм построения береговой линии внес элемент случайности, который, однако, не повлиял на основной вывод в отношении длины береговой линии. Поскольку предел
длина береговой линии за счет бесконечной изрезанности берега стремится к бесконечности. Процедура сглаживания береговой линии при переходе от более детального масштаба к менее детальному, т.е. согласно рис переходы от (д) к (г), от (г) к (в), от (в) к (б), дает одну и ту же величину: на три части длины — одну «бухту», а длина стремится к единичному значению.
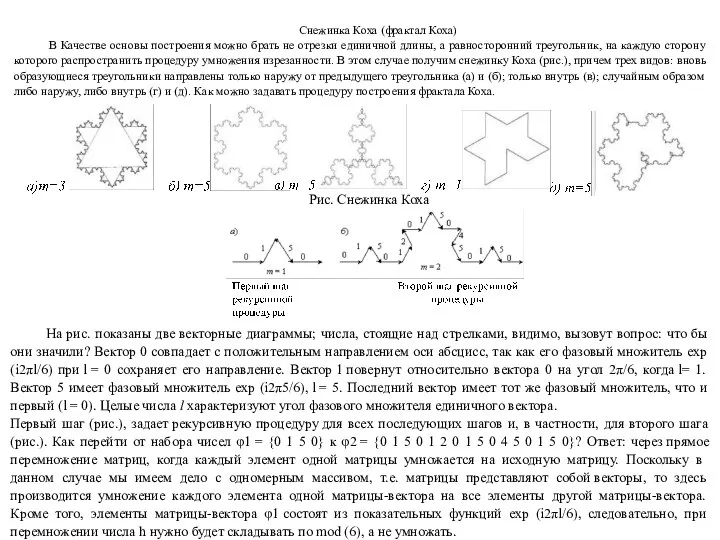
Снежинка Коха (фрактал Коха)
В Качестве основы построения можно брать не отрезки
Снежинка Коха (фрактал Коха)
В Качестве основы построения можно брать не отрезки
Рис. Снежинка Коха
На рис. показаны две векторные диаграммы; числа, стоящие над стрелками, видимо, вызовут вопрос: что бы они значили? Вектор 0 совпадает с положительным направлением оси абсцисс, так как его фазовый множитель exp (i2πl/6) при l = 0 сохраняет его направление. Вектор 1 повернут относительно вектора 0 на угол 2π/6, когда l= 1. Вектор 5 имеет фазовый множитель exp (i2π5/6), l = 5. Последний вектор имеет тот же фазовый множитель, что и первый (l = 0). Целые числа l характеризуют угол фазового множителя единичного вектора.
Первый шаг (рис.), задает рекурсивную процедуру для всех последующих шагов и, в частности, для второго шага (рис.). Как перейти от набора чисел φ1 = {0 1 5 0} к φ2 = {0 1 5 0 1 2 0 1 5 0 4 5 0 1 5 0}? Ответ: через прямое перемножение матриц, когда каждый элемент одной матрицы умножается на исходную матрицу. Поскольку в данном случае мы имеем дело с одномерным массивом, т.е. матрицы представляют собой векторы, то здесь производится умножение каждого элемента одной матрицы-вектора на все элементы другой матрицы-вектора. Кроме того, элементы матрицы-вектора φ1 состоят из показательных функций exp (i2πl/6), следовательно, при перемножении числа h нужно будет складывать по mod (6), а не умножать.
Губки Менгера.
Кроме одномерных есть и трёхмерные фракталы.
На рис. в трехмерном пространстве
Губки Менгера.
Кроме одномерных есть и трёхмерные фракталы.
На рис. в трехмерном пространстве
Губки Менгера используются как аналог множество Кантора в трёхмерном пространстве.








 Прогресс общества. Гендерный аспект
Прогресс общества. Гендерный аспект Презентация на тему "Нравственное воспитание школьников" - скачать презентации по Педагогике
Презентация на тему "Нравственное воспитание школьников" - скачать презентации по Педагогике Олимпиадные задачи. Динамическое программирование
Олимпиадные задачи. Динамическое программирование Модель создания корпоративного имиджа по Б. Джи и ее применение в российских условиях Выполнила: Давыдова Лена, 401 группа Руков
Модель создания корпоративного имиджа по Б. Джи и ее применение в российских условиях Выполнила: Давыдова Лена, 401 группа Руков The 10 most extravagant hats for the Royal Ascot races Royal
The 10 most extravagant hats for the Royal Ascot races Royal Международные экономические организации 1. Международные правительственные (межгосударственные) экономические организации. 2.
Международные экономические организации 1. Международные правительственные (межгосударственные) экономические организации. 2.  Понятие и причины текучести персонала. Понятие абсентеизма, способы снижения абсентеизма на предприятии
Понятие и причины текучести персонала. Понятие абсентеизма, способы снижения абсентеизма на предприятии 1 апреля - день шуток и смеха
1 апреля - день шуток и смеха Саяны
Саяны  Строительство египетских пирамид
Строительство египетских пирамид Имидж современного педагога
Имидж современного педагога Презентация Microsoft PowerPoint
Презентация Microsoft PowerPoint Продовольственная безопасность России. Горовых А.Е (Т-093)
Продовольственная безопасность России. Горовых А.Е (Т-093)  Halloween. Origins and Traditions
Halloween. Origins and Traditions Недостоверное декларирование: не правильное присвоение кода товара по ЕТН ВЭД ТС Выполнили студентки 3-го курса ФТД группы Т-1209
Недостоверное декларирование: не правильное присвоение кода товара по ЕТН ВЭД ТС Выполнили студентки 3-го курса ФТД группы Т-1209  обмен веществ в эритроцитах
обмен веществ в эритроцитах  Отличие работы одиночной сваи от группы свай ПГС-152 Крупский Глеб
Отличие работы одиночной сваи от группы свай ПГС-152 Крупский Глеб Народ манси
Народ манси Коммерческая тайна. Материал для сотрудников РИЦ. КУП для бюджетных организаций
Коммерческая тайна. Материал для сотрудников РИЦ. КУП для бюджетных организаций Формы поведения
Формы поведения  Экспериментальная и инновационная работа с курсом «Проектная дея
Экспериментальная и инновационная работа с курсом «Проектная дея Презентация1
Презентация1 Чтобы быть хорошим преподавателем, нужно любить то, что преподаешь, и любить тех кому преподаешь. В. Ключевс
Чтобы быть хорошим преподавателем, нужно любить то, что преподаешь, и любить тех кому преподаешь. В. Ключевс Презентация Эмоции
Презентация Эмоции  Технология повышения среднего чека в магазине
Технология повышения среднего чека в магазине События и делегаты
События и делегаты Знать много языков - история моей страны
Знать много языков - история моей страны Раскладные механизмы диванов
Раскладные механизмы диванов