Содержание
- 2. Кафедра биологической и медицинской физики — одна из первых кафедр Военно-медицинской академии и старейшая кафедра физики
- 3. Здание Естественно-исторического института
- 4. Первым профессором кафедры стал Василий Владимирович Петров (1761—1834) — знаменитый русский ученый-естествоиспытатель, заложивший основы преподавания экспериментальной
- 5. 1. Определение функции, числовых промежутков и окрестностей точек. Некоторые свойства функций и их графиков.
- 6. Пусть X, У — некоторые множества, элементами которых являются некоторые числа. Если каждому числу х Є
- 7. Переменная х называется независимой переменной или аргументом, а переменная у называется зависимой переменной (от х) или
- 8. Множество X — область изменения аргумента — называется областью определения функции. Множество У, содержащее все значения,
- 9. Множества X и Y часто являются конечными или бесконечными промежутками:
- 10. а) конечные промежутки: Открытый интервал (a,b): множество вещественных чисел, удовлетворяющих неравенствам a Замкнутый интервал (или отрезок)
- 11. б) бесконечные промежутки: (-∞, +∞) = R – множество всех вещественных чисел. Аналогично, возможны промежутки (а,+∞),
- 12. Пусть x0 – любое действительное число (точка на числовой прямой). Окрестностью точки х0 называется любой интервал
- 13. 1) Графический. Правило, по которому можно находить у, зная х, может быть задано графиком функции. Графиком
- 14. Пример. Графиком функции у = х2 является парабола, ось симметрии которой совпадает с положительной полуосью ординат,
- 15. Функцию можно задавать также с помощью таблицы или формулы (аналитически). 2) Табличный способ применяется на практике
- 16. Основные характеристики функции: монотонность, ограниченность, четность (нечетность), периодичность.
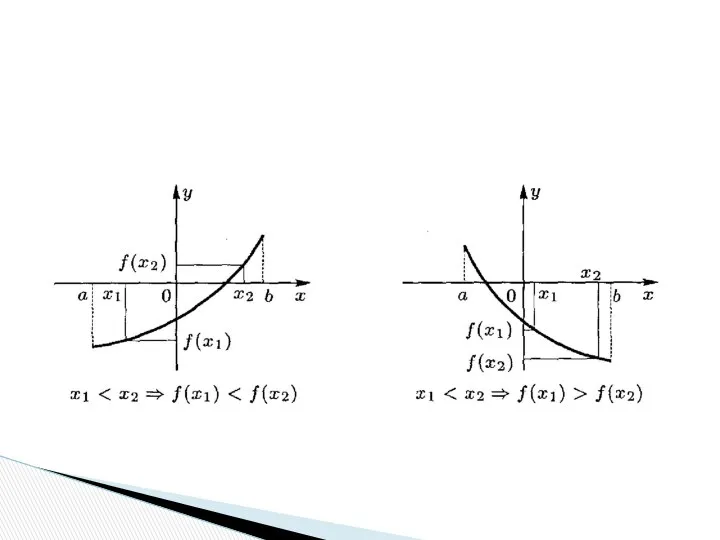
- 17. Определение. Функция называется возрастающей (убывающей) в интервале, если большему значению аргумента из этого интервала соответствует большее
- 19. Определение. Интервал независимой переменной, в котором функция возрастает (убывает), называется интервалом возрастания (убывания). Как интервал возрастания,
- 20. Определение. Функция называется четной, если при изменении знака допустимого аргумента значение функции не изменяется. Функция называется
- 21. Таким образом, если функция f(x) — четная, то для всех х из ее области определения должно
- 22. Четные или нечетные функции должны быть обязательно определены в области, симметричной относительно начала координат. При этом
- 23. Не все функции являются четными либо нечетными; функции, не являющиеся ни четными, ни нечетными, будем называть
- 24. Определение. Функция f(x) называется периодической, если существует такое положительное число а, что f(x + a) =
- 25. Примером периодической функции служит определенная на всей оси функция у = cos x, период которой равен
- 26. 2. Сложная функция. Обратная функция.
- 27. Определение. Сложной функцией называется функция, аргумент которой также является функцией, т.е. F(x) = f(φ(x)). Чтобы сосчитать
- 28. При этом область определения функции F(x) следует выбирать таким образом, чтобы промежуточное множество U, с одной
- 29. Пример. Рассмотрим сложную функцию у = lg(1- x2). Здесь у = f(u) = lgu, в то
- 30. Рассмотрим функцию с областью определения X и областью значений Y. Предположим, что каждому значению у ε
- 31. Функции f и φ с вышеперечисленными свойствами называются взаимно-обратными, а функция φ называется обратной по отношению
- 32. Между графиками функций у = f(x) и у = φ(х) имеется простая связь: график обратной функции
- 34. 3. Элементарные функции. Тригонометрические функции. Обратные тригонометрические функции.
- 35. Определение. Основными элементарными функциями являются: 1) степенная функция: у = хn, где n — действительное число,
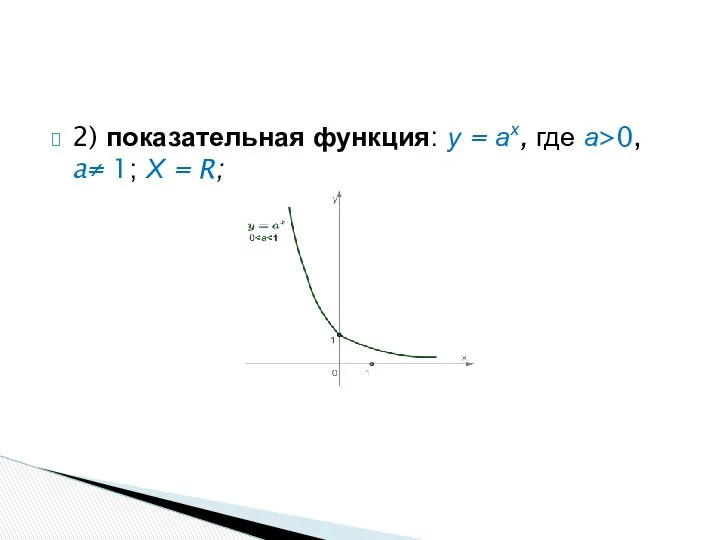
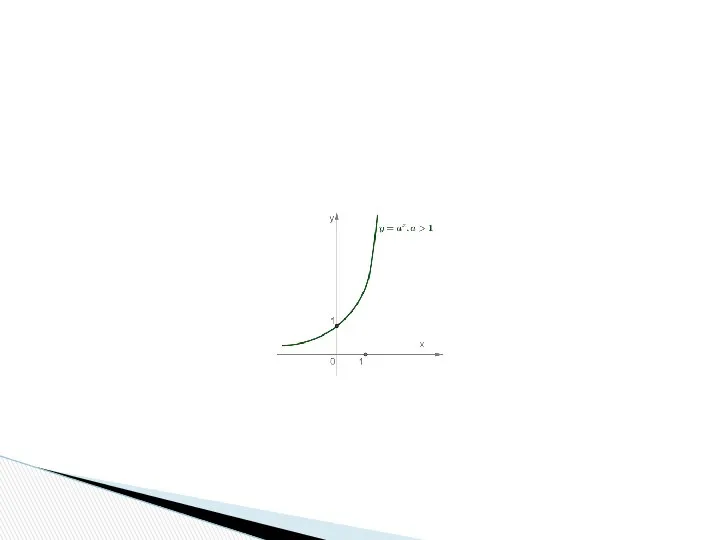
- 36. 2) показательная функция: у = ах, где а>0, a≠ 1; Х = R;
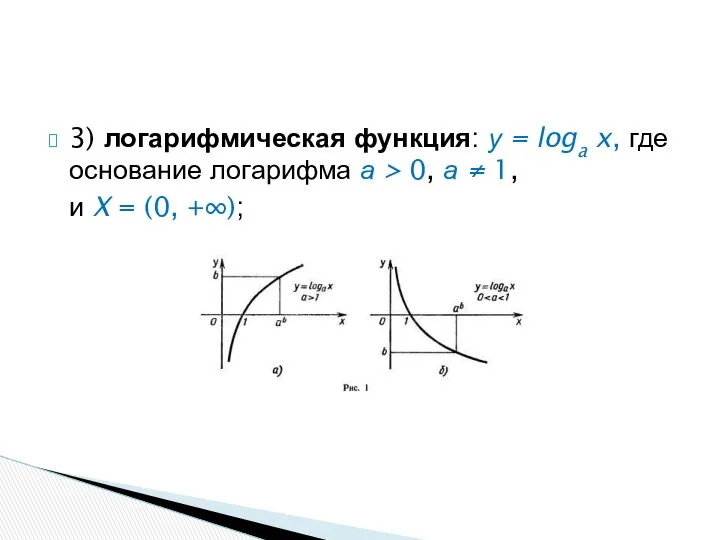
- 38. 3) логарифмическая функция: у = loga x, где основание логарифма а > 0, а ≠ 1,
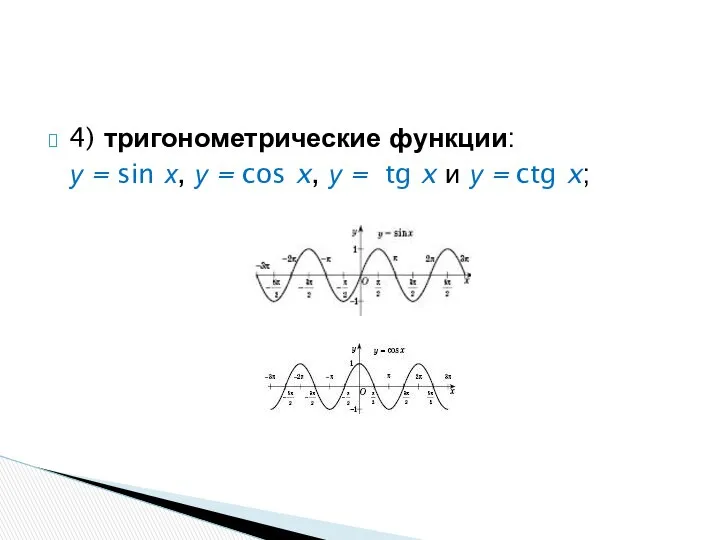
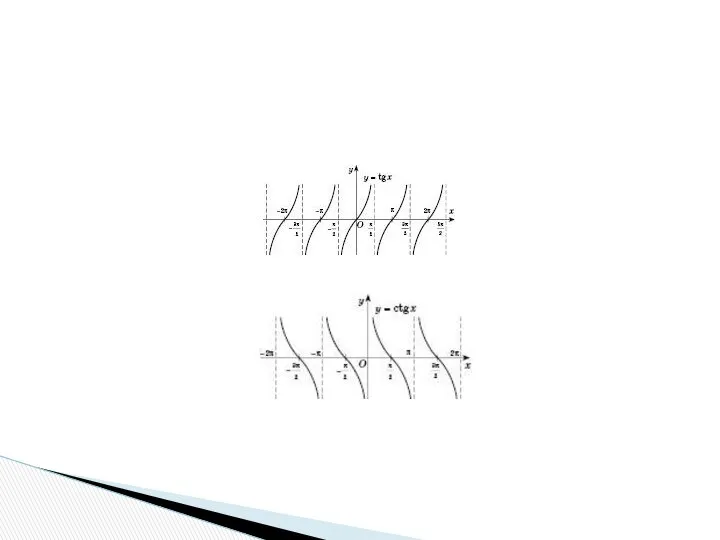
- 39. 4) тригонометрические функции: у = sin х, у = cos x, у = tg x и
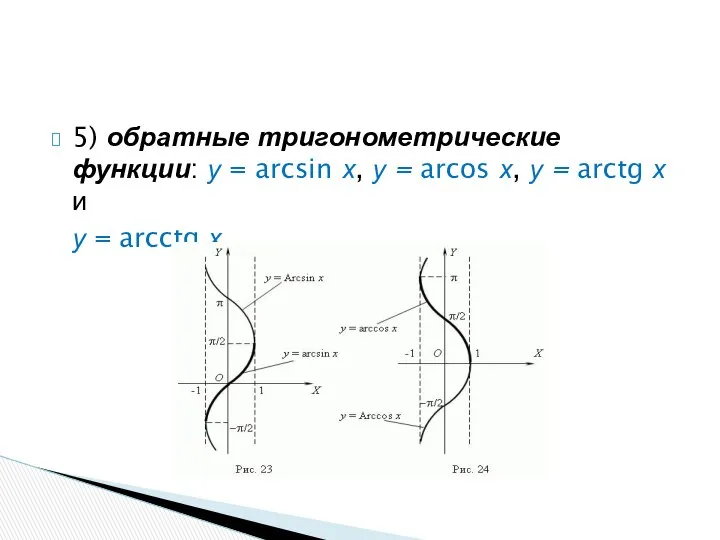
- 41. 5) обратные тригонометрические функции: у = arcsin х, у = arcos х, у = arctg х
- 42. Пример. Пусть задана функция f(x) = , определенная при всех значениях х, кроме х = 1.
- 43. Исследуем поведение функции при значениях х, мало отличающихся от 1. Для этого составим таблицу значений функции
- 44. Чем ближе х приближается к 1, тем ближе значения f(x) к 2. В подобных случаях говорят,
- 45. Определение. Пусть функция f(x) определена в некоторой окрестности точки x0, кроме, может быть, самой точки x0.
- 46. В приводимых ниже теоремах будем считать, что функции f(x) и g(x) имеют общую область определения, содержащую
- 47. Теорема 1 (о единственности предела функции). Функция не может иметь более одного предела. Следствие. Если две
- 48. Теорема 2. Если функции f(x) и g(x) имеют пределы в точке x0, то: 1) предел алгебраической
- 49. 2) предел произведения функций равен произведению пределов сомножителей, т.е.
- 50. Теорема 3. Предел частного двух функций равен частному от деления предела делимого на предел делителя, если
- 51. Следствие 1. Предел постоянной равен самой постоянной, т.е. Следствие 2. Постоянный множитель можно выносить за знак
- 52. Следствие 2. Постоянный множитель можно выносить за знак предела, т.е.
- 53. Для решения примеров используются следующие пределы: (первый классический предел) (второй классический предел) Специальные пределы
- 54. При решении примеров полезно иметь в виду следующие равенства:
- 55. Рассмотрим функцию у = f(х), определенную в интервале [а, b]. Пусть х0 и х — два
- 56. Приращением Δу функции у = f(х), соответствующим приращению Δх аргумента х в точке х0, называется разность
- 57. Второе определение непрерывности функции: Функция называется непрерывной в данной точке, если в этой точке бесконечно малому
- 58. Определение. Функция f(x) называется непрерывной в интервале, если эта функция непрерывна в каждой точке этого интервала.
- 59. Непрерывность функции в точке x0 равносильна ее непрерывности в этой точке одновременно слева и справа, то
- 60. Если в точке x0 не выполняется хотя бы одно условие, то в этой точке функция терпит
- 63. Скачать презентацию














































![Рассмотрим функцию у = f(х), определенную в интервале [а, b]. Пусть](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/1304746/slide-54.jpg)





 Зимний курс теоретических тренировок для летнего спортивного ориентирования. Упражнение Relative Altitude 1 2017
Зимний курс теоретических тренировок для летнего спортивного ориентирования. Упражнение Relative Altitude 1 2017 Работа с файлами
Работа с файлами Социально-психологическая работа с одаренными детьми Педагог-психолог Слезкин Р.Ю.
Социально-психологическая работа с одаренными детьми Педагог-психолог Слезкин Р.Ю. Словарное слово «ПОНЕДЕЛЬНИК
Словарное слово «ПОНЕДЕЛЬНИК 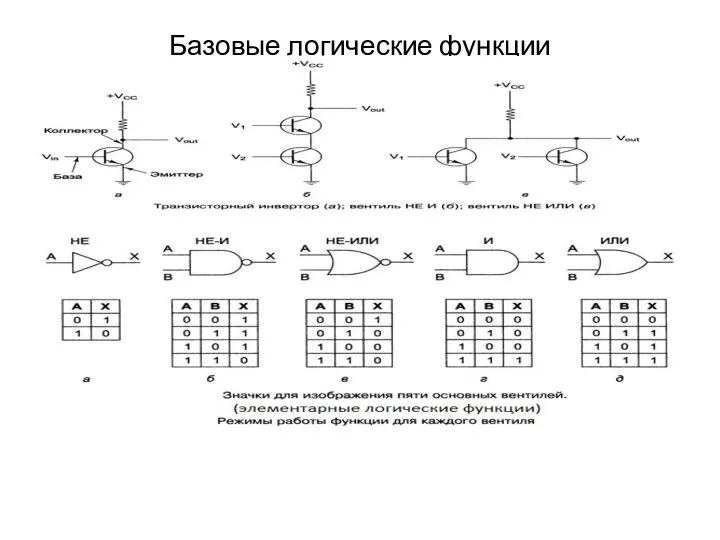 Базовые логические функции. Основные понятия алгебры логики
Базовые логические функции. Основные понятия алгебры логики Презентация по МХК Художественная культура Древней Руси
Презентация по МХК Художественная культура Древней Руси  ЯП-алфавит Типы данных выражения операции
ЯП-алфавит Типы данных выражения операции  Автор материалов: Безруких Марьяна Михайловна Трудности обучения письму и чтению в начальной школе. Род
Автор материалов: Безруких Марьяна Михайловна Трудности обучения письму и чтению в начальной школе. Род Омск
Омск  Эвольвентные поверхности. Основы теории режущих инструментов
Эвольвентные поверхности. Основы теории режущих инструментов Логистическая цепочка создания стоимости Исаева Катерина Казакова Катя ДС - 07
Логистическая цепочка создания стоимости Исаева Катерина Казакова Катя ДС - 07  Национальный проект: культура
Национальный проект: культура . Уход за волосами
. Уход за волосами Конспект. Вимоги до конспекту
Конспект. Вимоги до конспекту Бешенство у человека. Департамент здравоохранения города Москвы ГБОУ СПО Медицинский колледж №4
Бешенство у человека. Департамент здравоохранения города Москвы ГБОУ СПО Медицинский колледж №4 Ag Artificial Gravity
Ag Artificial Gravity Искусственное вскармливание
Искусственное вскармливание  ВИДЫ ОЦЕНКИ
ВИДЫ ОЦЕНКИ Введение в PHP. Знакомство с языком
Введение в PHP. Знакомство с языком Орденская система в России
Орденская система в России Студенческий спортивный клуб КНИТУ «KRONOS»
Студенческий спортивный клуб КНИТУ «KRONOS» Дэниэл Трейсман, книга «Возвращение: Путь России от Горбачёва до Медведева»
Дэниэл Трейсман, книга «Возвращение: Путь России от Горбачёва до Медведева» Управление качеством проекта. Лекция 8
Управление качеством проекта. Лекция 8 Введение в детскую офтальмологию. Клинические аспекты анатомии. Основные функции органа зрения
Введение в детскую офтальмологию. Клинические аспекты анатомии. Основные функции органа зрения Симплексный метод линейного программирования
Симплексный метод линейного программирования Правоохранительные органы осуществляющие следственные функции
Правоохранительные органы осуществляющие следственные функции Тест на знання теорії
Тест на знання теорії Первоочередная диагностика пострадавшего
Первоочередная диагностика пострадавшего