Содержание
- 2. 7. Парабола и её каноническое уравнение
- 3. 7. Парабола и её каноническое уравнение Параболой называется геометрическое место точек, для каждой из которых расстояние
- 4. 7. Парабола и её каноническое уравнение Расстояние от фокуса параболы до её директрисы называется параметром параболы.
- 5. 7. Парабола и её каноническое уравнение Расстояние от фокуса параболы до её директрисы называется параметром параболы.
- 6. F
- 7. F
- 8. F
- 9. F D
- 10. F D O
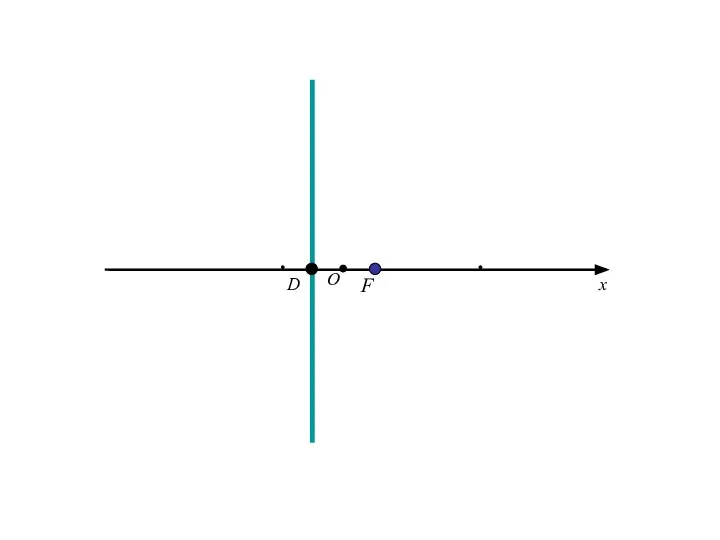
- 11. F D O x
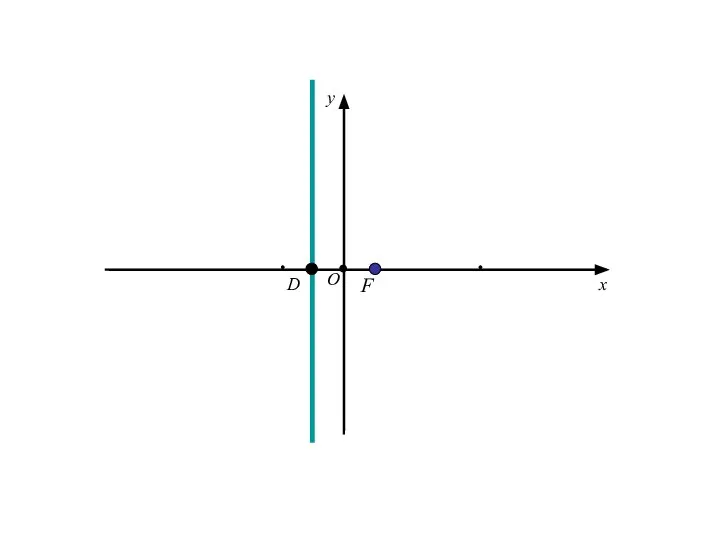
- 12. F D O x y
- 13. Расстояние FD обозначим р (параметр параболы).
- 14. Расстояние FD обозначим р (параметр параболы). тогда в выбранной системе координат фокус F будет иметь координаты
- 15. Расстояние FD обозначим р (параметр параболы). тогда в выбранной системе координат фокус F будет иметь координаты
- 16. Расстояние FD обозначим р (параметр параболы). тогда в выбранной системе координат фокус F будет иметь координаты
- 17. Расстояние FD обозначим р (параметр параболы). тогда в выбранной системе координат фокус F будет иметь координаты
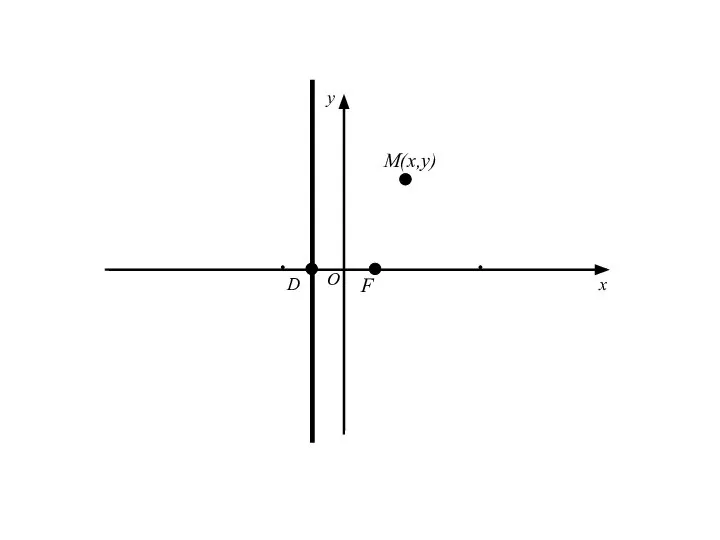
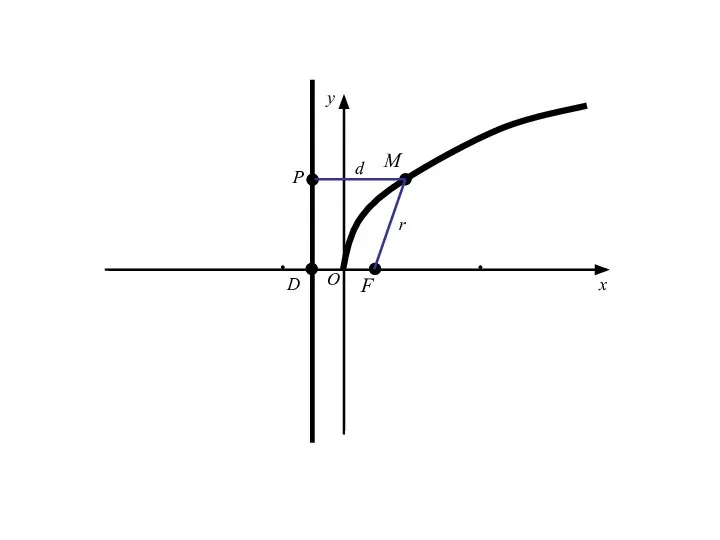
- 18. M(x,y) F D O x y
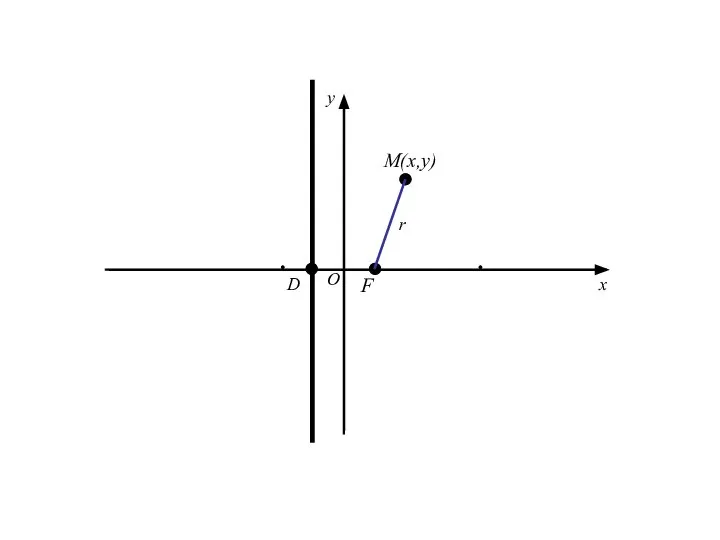
- 19. M(x,y) F D O x y r
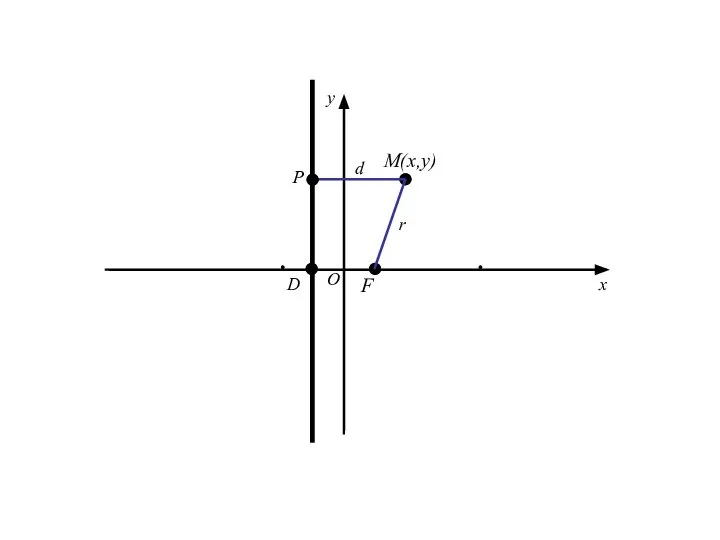
- 20. M(x,y) F D O x y r P d
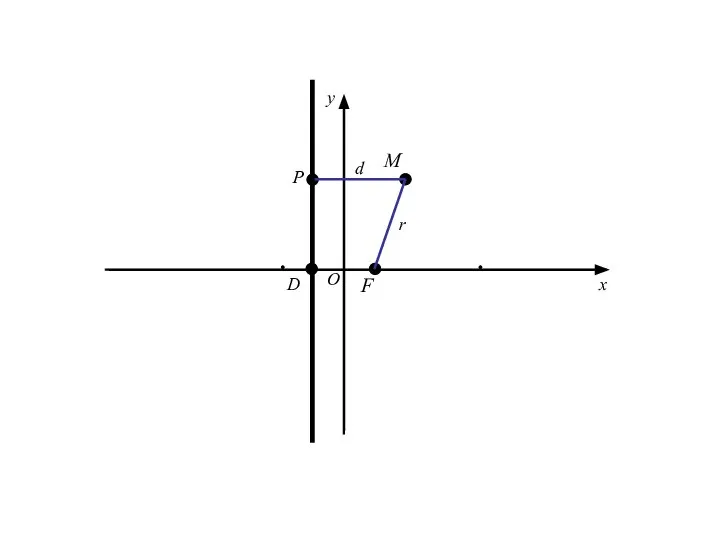
- 21. Точка M(x;y) лежит на данной параболе тогда и только тогда, когда r = d
- 22. Точка M(x;y) лежит на данной параболе тогда и только тогда, когда r = d r=|FM|=
- 23. Точка M(x;y) лежит на данной параболе тогда и только тогда, когда r = d r=|FM|=
- 24. Точка M(x;y) лежит на данной параболе тогда и только тогда, когда r = d r=|FM|= d=|PM|=
- 25. Точка M(x;y) лежит на данной параболе тогда и только тогда, когда r = d r=|FM|= d=|PM|=
- 26. Точка M(x;y) лежит на данной параболе тогда и только тогда, когда r = d r=|FM|= d=|PM|=
- 30. Каноническое уравнение параболы
- 31. 8. Исследование формы параболы
- 32. 8. Исследование формы параболы Т.к. ордината у в каноническом уравнении параболы входит во 2-й степени, то
- 33. 8. Исследование формы параболы Т.к. ордината у в каноническом уравнении параболы входит во 2-й степени, то
- 34. 8. Исследование формы параболы Т.к. ордината у в каноническом уравнении параболы входит во 2-й степени, то
- 35. 8. Исследование формы параболы Т.к. ордината у в каноническом уравнении параболы входит во 2-й степени, то
- 36. 8. Исследование формы параболы Т.к. ордината у в каноническом уравнении параболы входит во 2-й степени, то
- 37. 8. Исследование формы параболы Всякая прямая пересекает параболу не более чем в двух точках
- 38. 8. Исследование формы параболы Всякая прямая пересекает параболу не более чем в двух точках (т.к. прямая
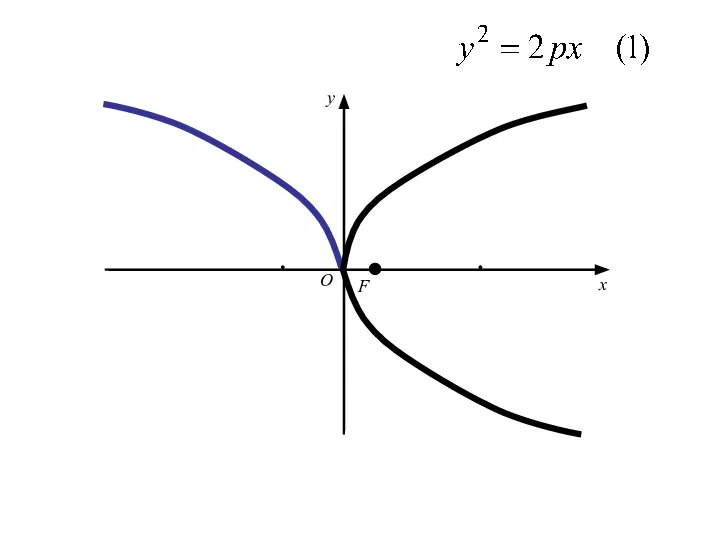
- 39. Из (1) ⇒, что x≥0
- 40. Из (1) ⇒, что x≥0 (т. к. p>0, а
- 41. Из (1) ⇒, что x≥0 (т. к. p>0, а Разрешая уравнение (1) относительно у
- 42. Из (1) ⇒, что x≥0 (т. к. p>0, а Разрешая уравнение (1) относительно у и беря
- 43. Из (1) ⇒, что x≥0 (т. к. p>0, а Разрешая уравнение (1) относительно у и беря
- 44. Из (1) ⇒, что x≥0 (т. к. p>0, а Разрешая уравнение (1) относительно у и беря
- 45. Из (1) ⇒, что x≥0 (т. к. p>0, а Разрешая уравнение (1) относительно у и беря
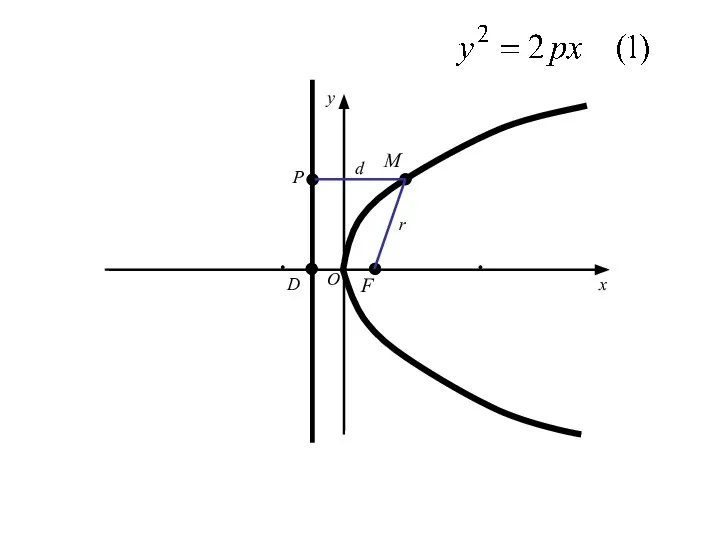
- 46. M F D O x y P r d
- 47. M F D O x y P r d
- 48. M F D O x y P r d
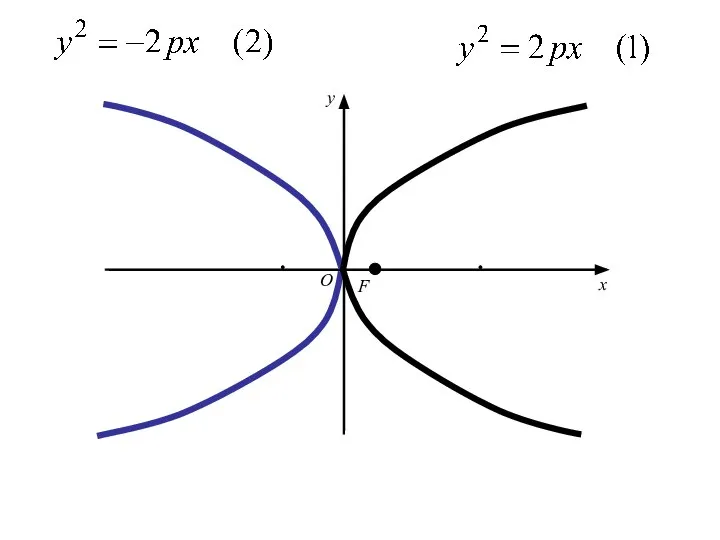
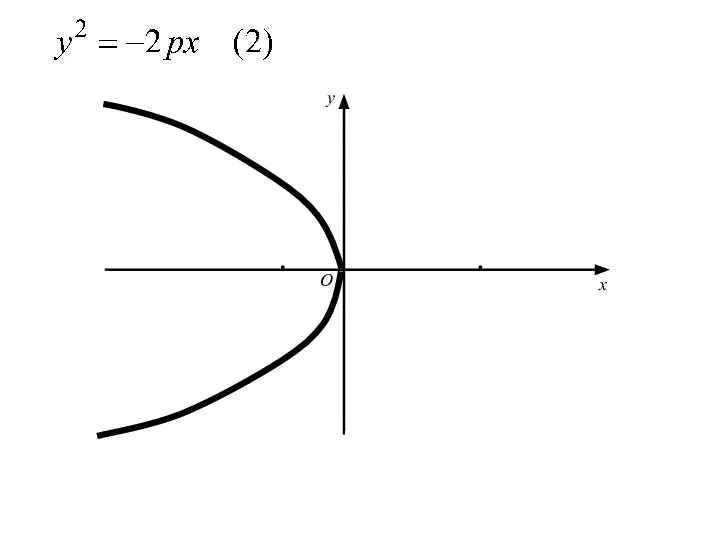
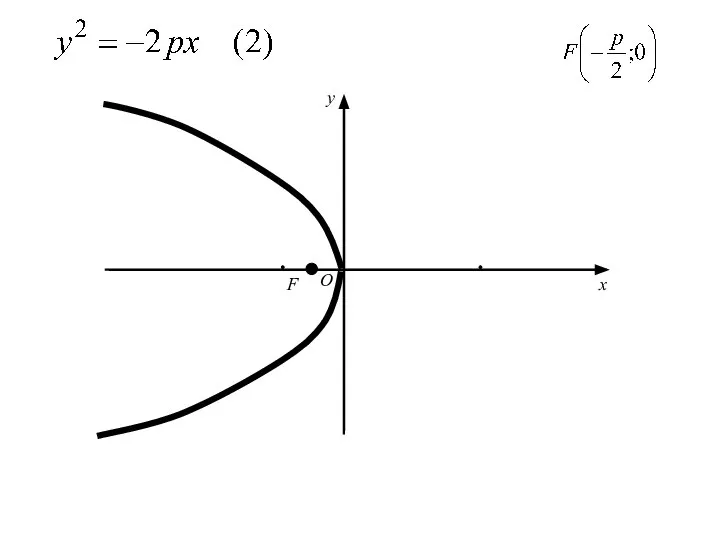
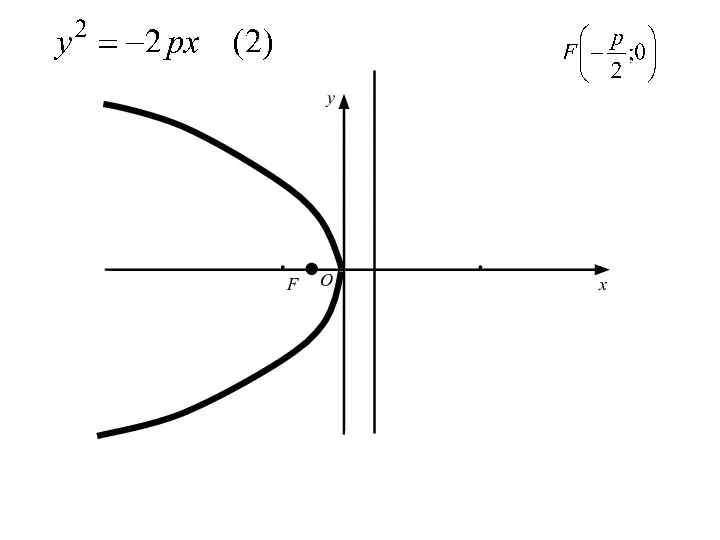
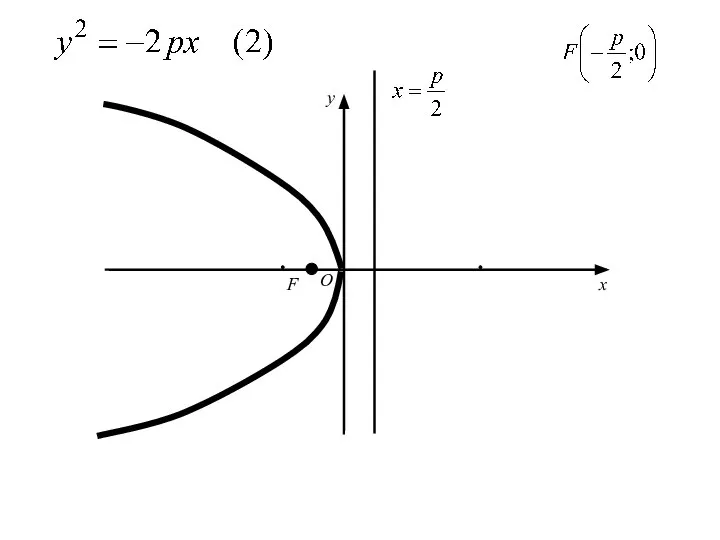
- 49. Уравнение , где р>0,
- 50. Уравнение , где р>0, сводиться к уравнению (1) заменой x на −x,
- 51. Уравнение , где р>0, сводиться к уравнению (1) заменой x на −x, т. е. путём преобразования
- 52. Уравнение , где р>0, сводиться к уравнению (1) заменой x на −x, т. е. путём преобразования
- 53. F O x y
- 54. F O x y
- 55. F O x y
- 56. O x y
- 57. F O x y
- 58. F O x y
- 59. F O x y
- 60. F O x y
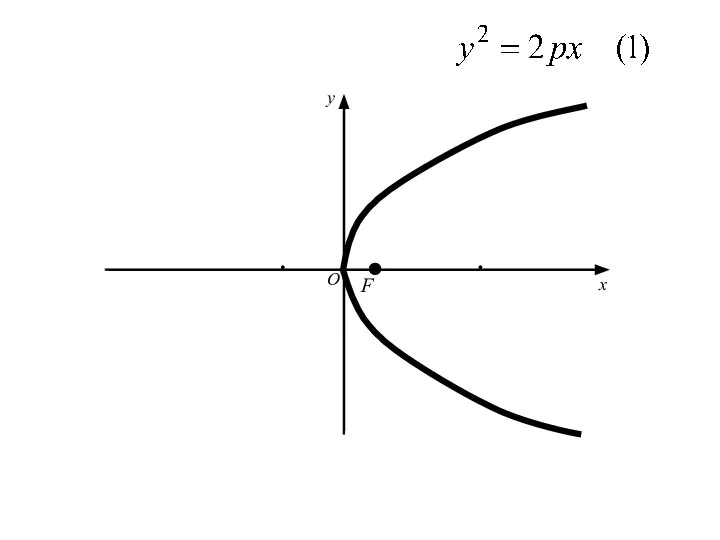
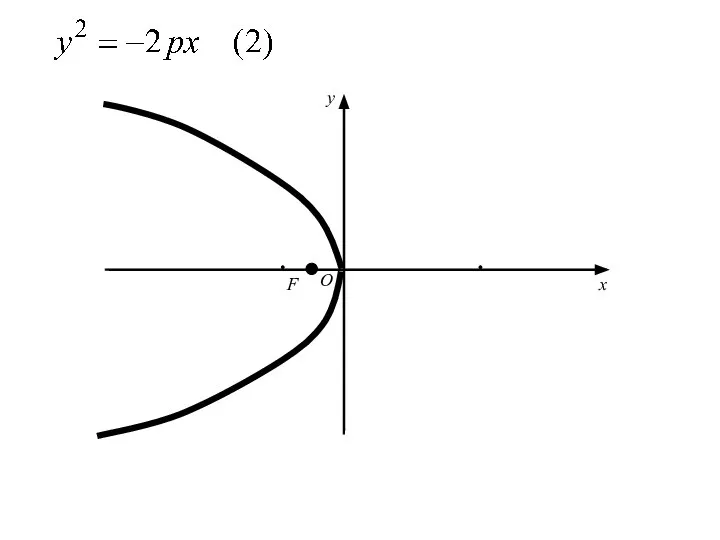
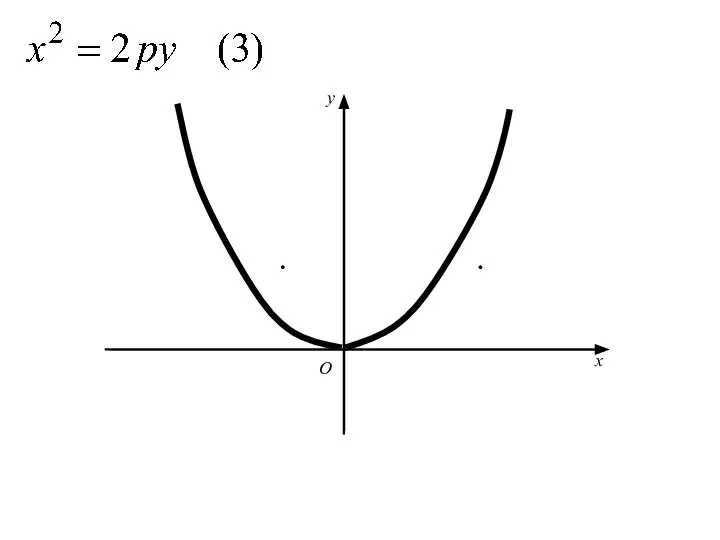
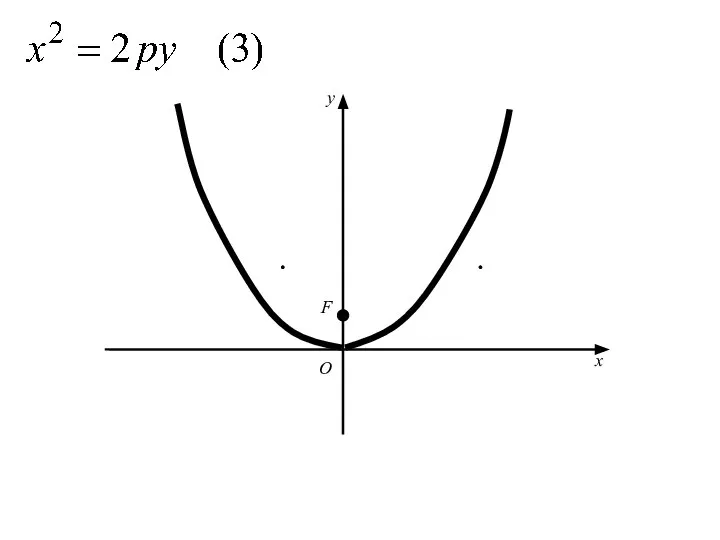
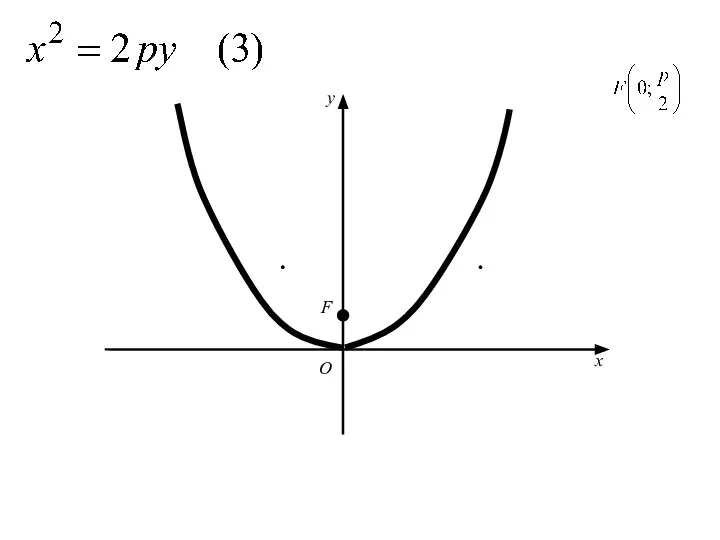
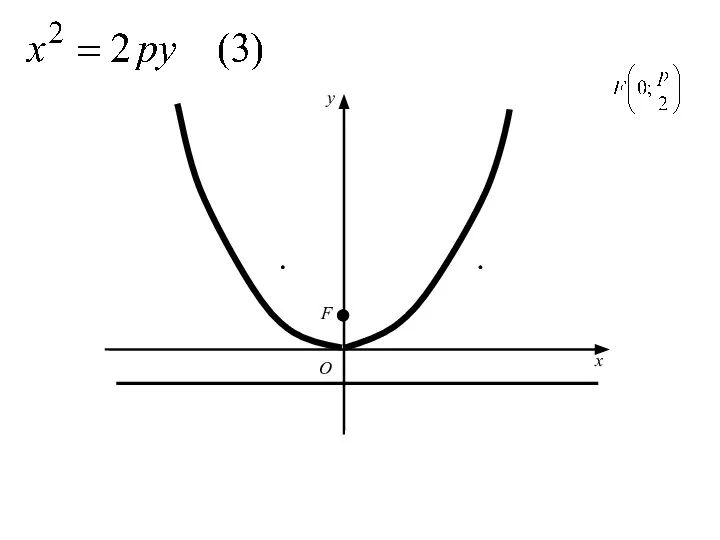
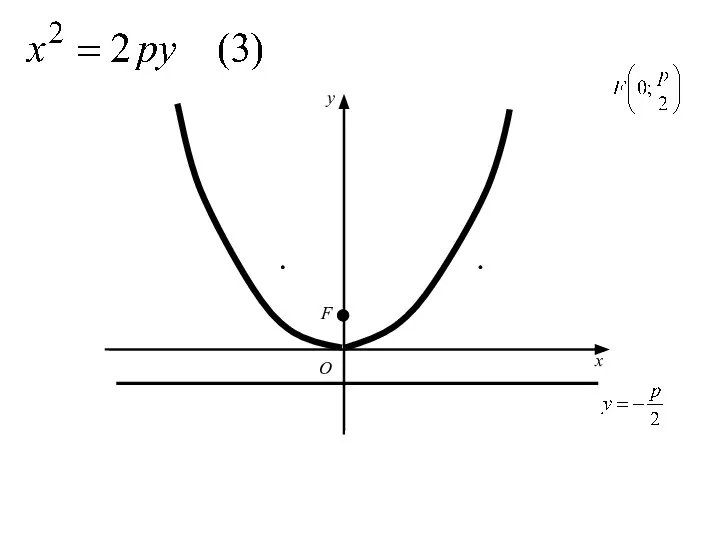
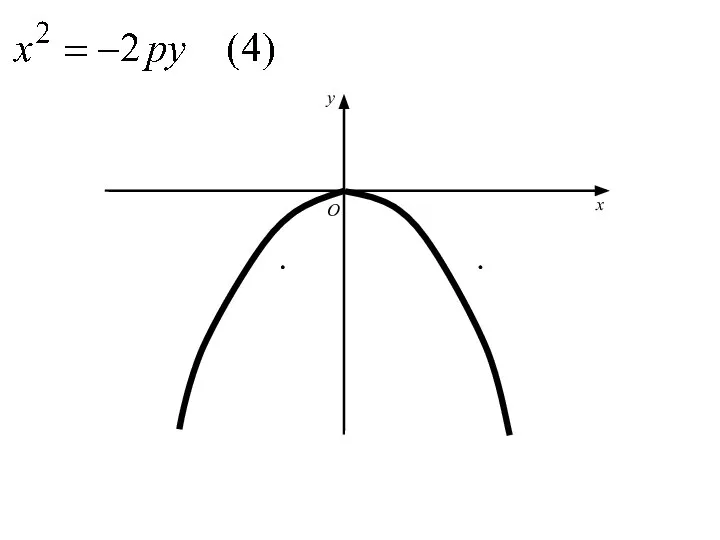
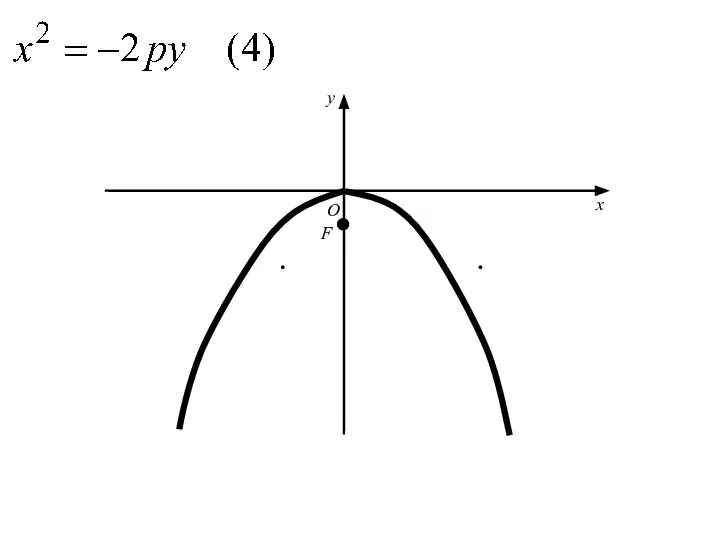
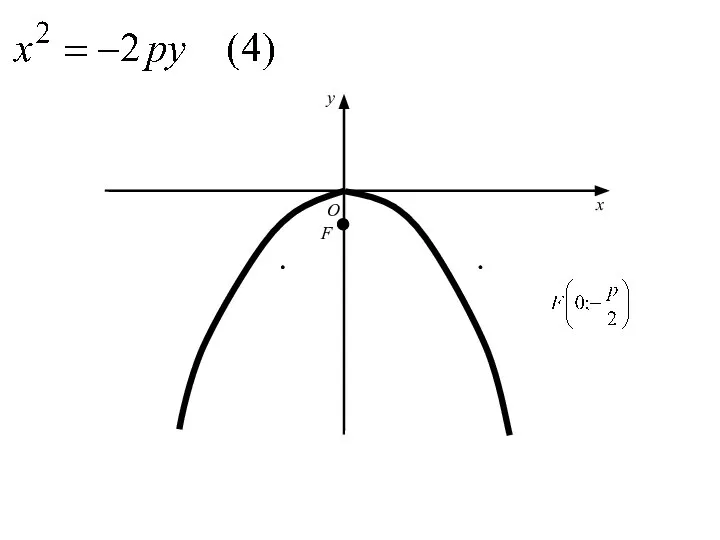
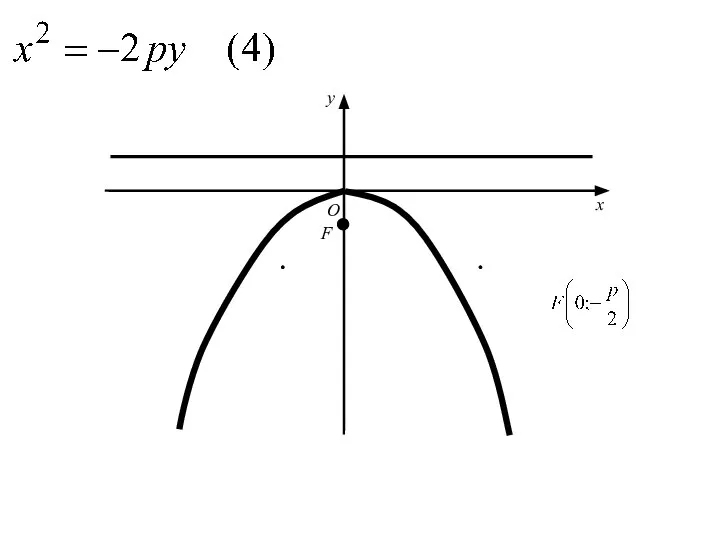
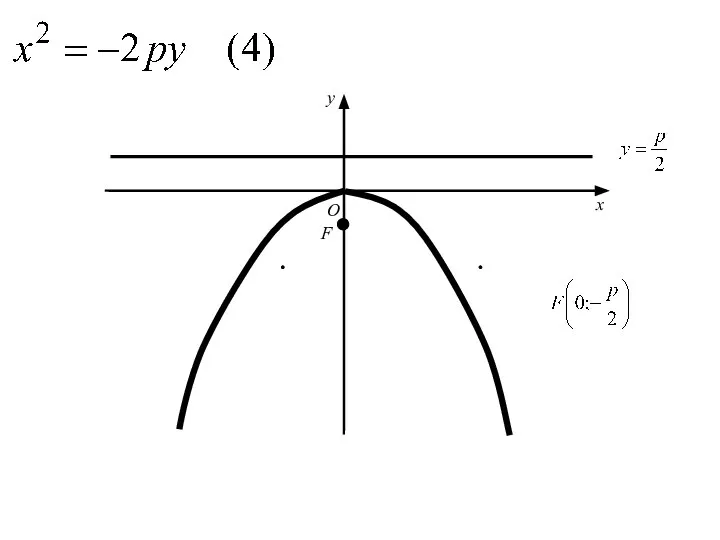
- 61. Аналогичными рассуждениями устанавливаем, что каждое из уравнений где p>0 определяет параболу с вершиной в начале координат
- 62. O x y
- 63. F O x y
- 64. F O x y
- 65. F O x y
- 66. F O x y
- 67. O x y
- 68. O x y F
- 69. O x y F
- 70. O x y F
- 71. O x y F
- 76. Самостоятельно изучить вопросы по данной теме: Уравнение касательной к параболе Оптическое свойство параболы
- 77. 9.Уравнение эллипса, параболы и гиперболы в полярных координатах.
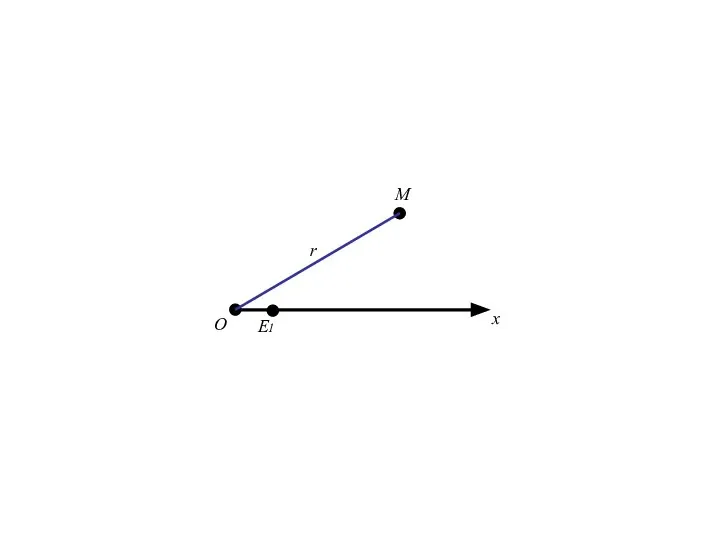
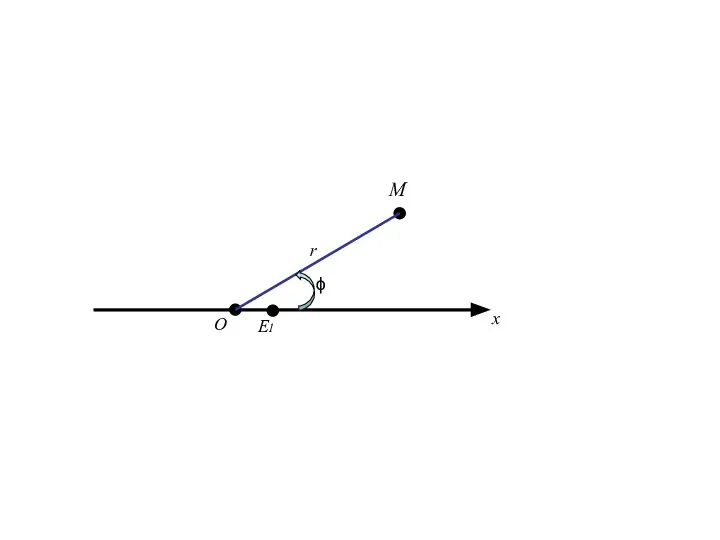
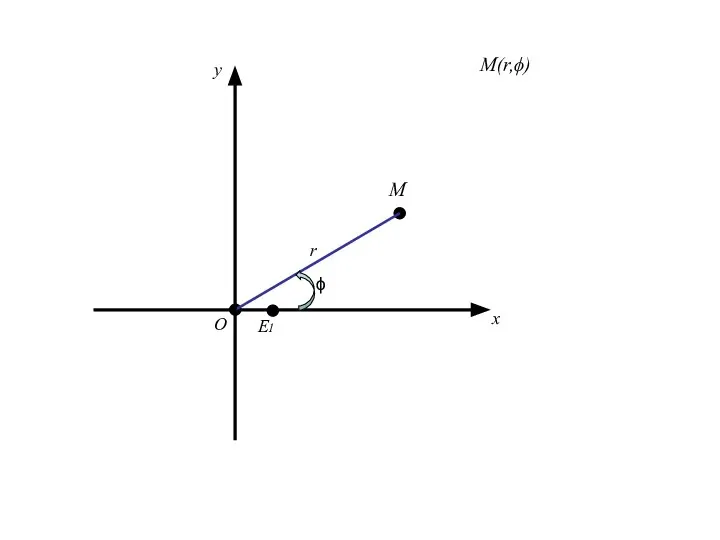
- 78. Полярная система координат на плоскости. Говорят, что на плоскости введена полярная система координат, если эта плоскость
- 79. О
- 80. О x
- 81. О x E1
- 82. О x E1 M
- 83. О x E1 M r
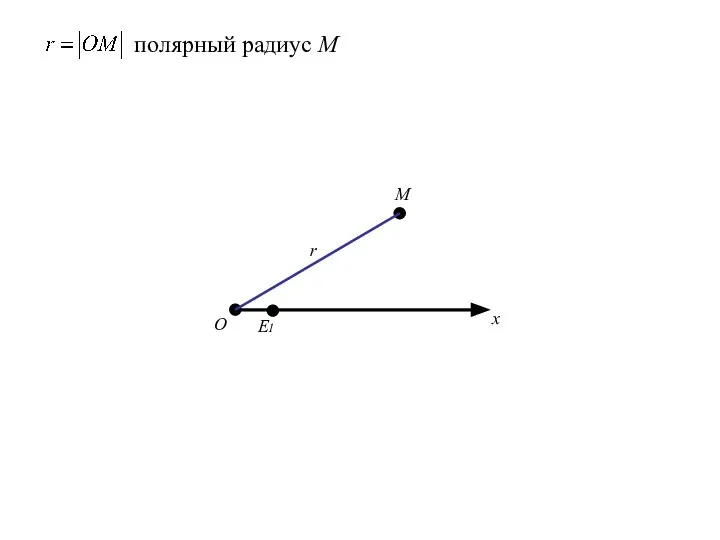
- 84. О x E1 M r полярный радиус М
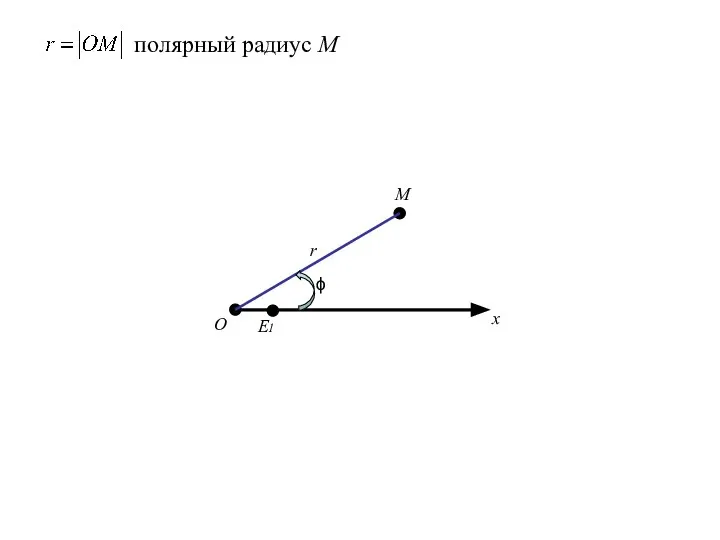
- 85. О x E1 M r полярный радиус М ϕ
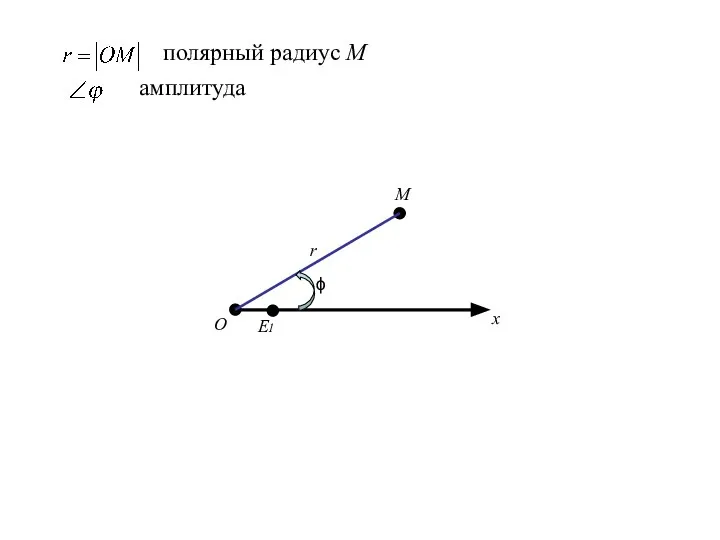
- 86. О x E1 M r полярный радиус М амплитуда ϕ
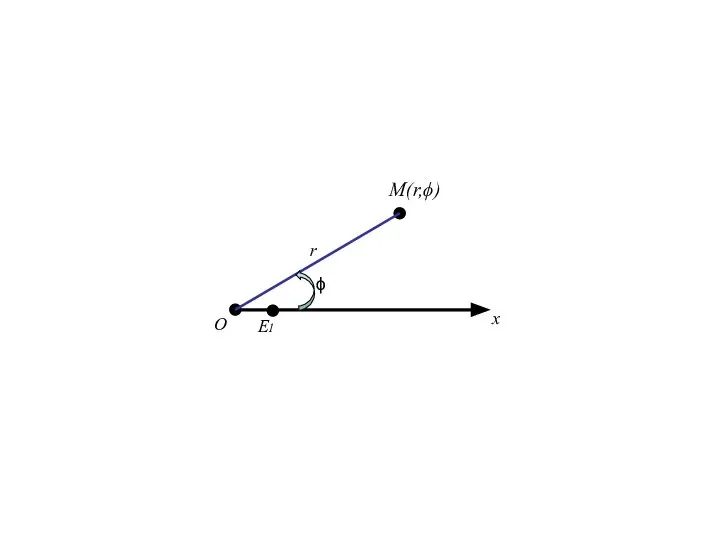
- 87. О x E1 r ϕ M(r,ϕ)
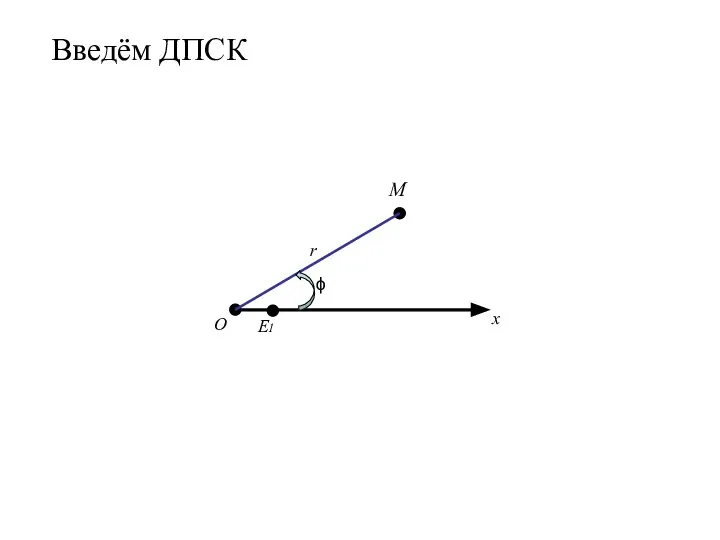
- 88. О x E1 r Введём ДПСК ϕ M
- 89. О x E1 r ϕ M
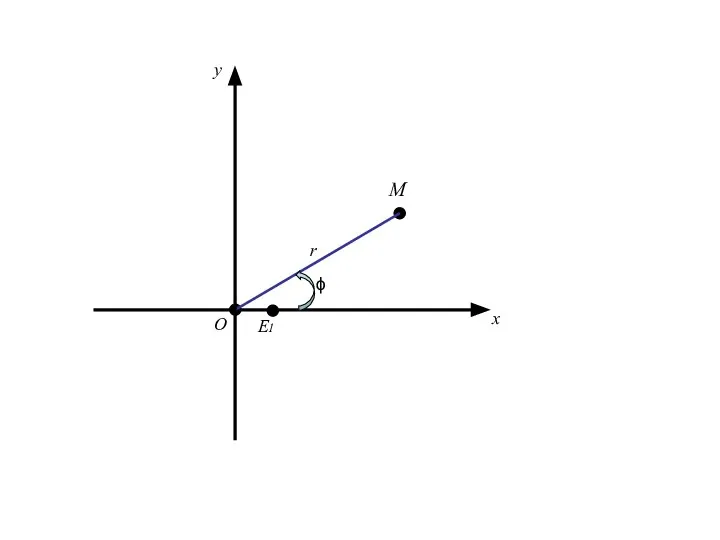
- 90. О x E1 r ϕ M y
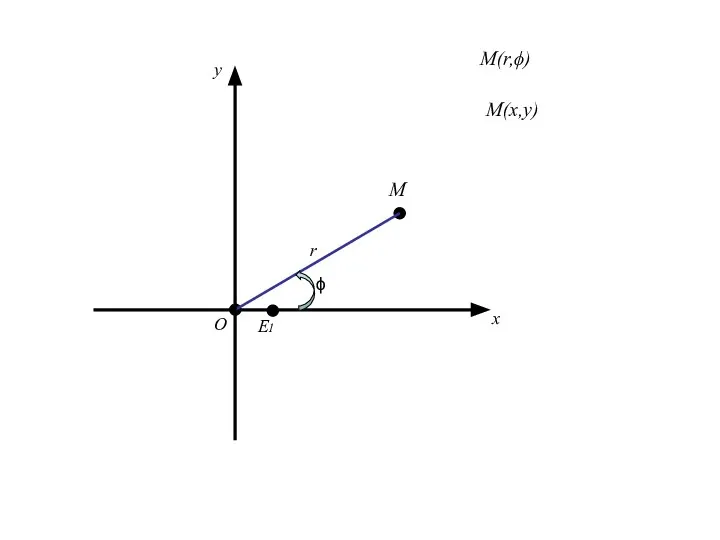
- 91. О x E1 r ϕ M y M(r,ϕ)
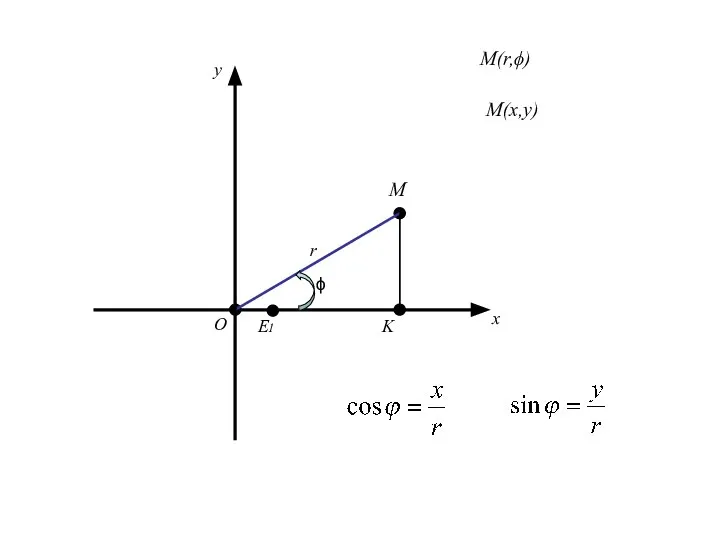
- 92. О x E1 r ϕ M y M(x,y) M(r,ϕ)
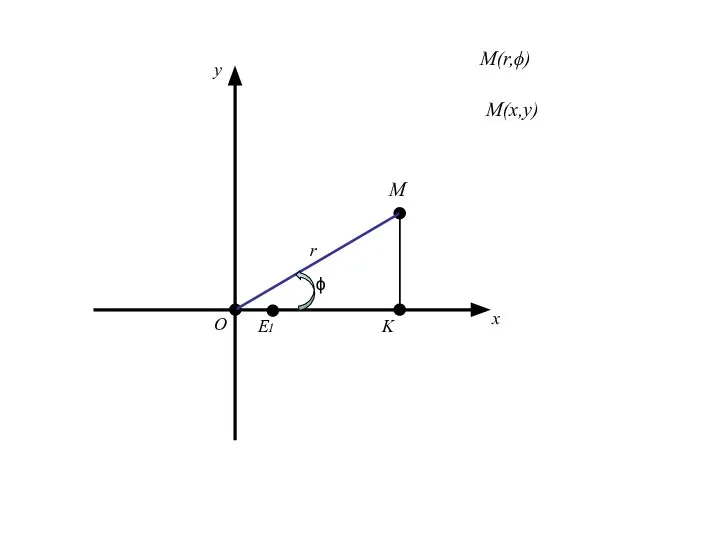
- 93. О x E1 r ϕ M y M(x,y) M(r,ϕ) K
- 94. О x E1 r ϕ M y M(x,y) M(r,ϕ) K
- 95. О x E1 r ϕ M y M(x,y) M(r,ϕ) K
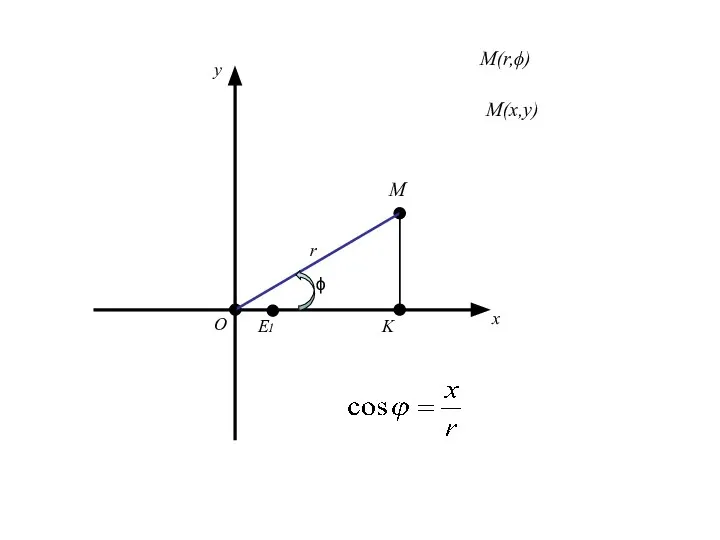
- 96. Из Получаем (1)
- 97. Из Получаем (1) Так как (2)
- 98. Из Получаем (1) Так как (2) то (3)
- 99. Формулы (1) позволяют вычислить декартовые прямоугольные координаты х, у точки М по её полярным координатам ϕ,r.
- 100. Формулы (1) позволяют вычислить декартовые прямоугольные координаты х, у точки М по её полярным координатам ϕ,r.
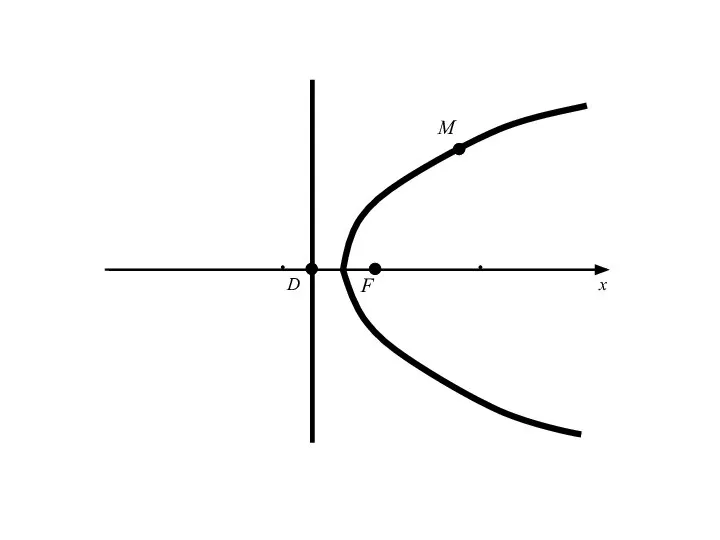
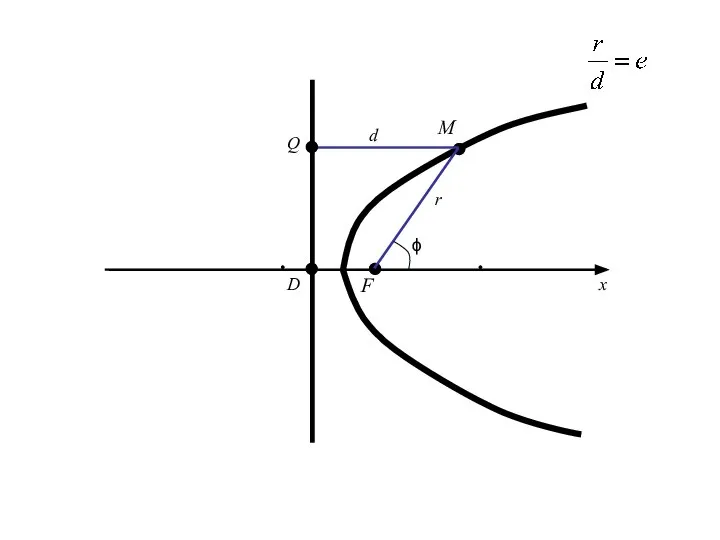
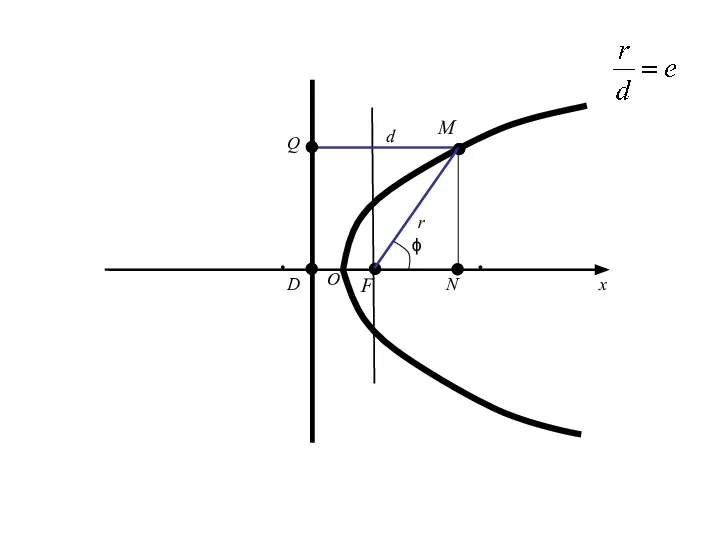
- 101. Полярное уравнение эллипса, гиперболы и параболы Пусть L-какая-нибудь из изученных нами линий второго порядка, (если L-гипербола,
- 102. Полярное уравнение эллипса, гиперболы и параболы Пусть L-какая-нибудь из изученных нами линий второго порядка, (если L-гипербола,
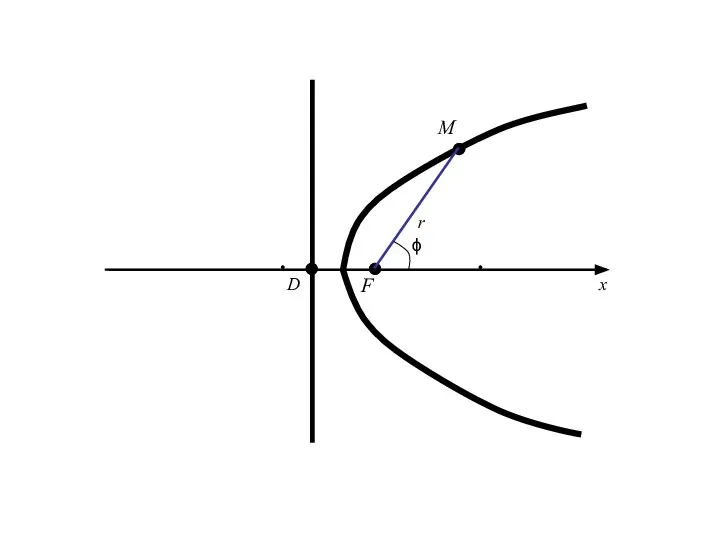
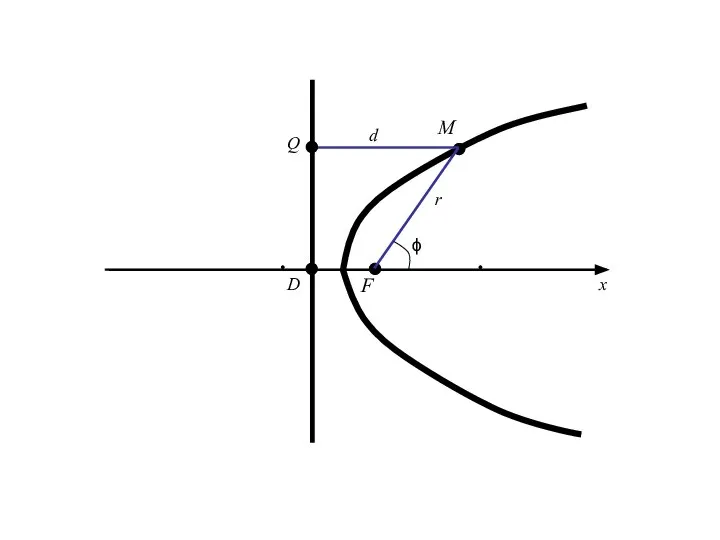
- 103. Введем полярную систему координат, совмещая полюс с фокусом F (в случае гиперболы берем фокус ближайшей к
- 104. M F D x
- 105. M F D x r ϕ
- 106. M F D x r d Q ϕ
- 107. M F D x r d Q ϕ
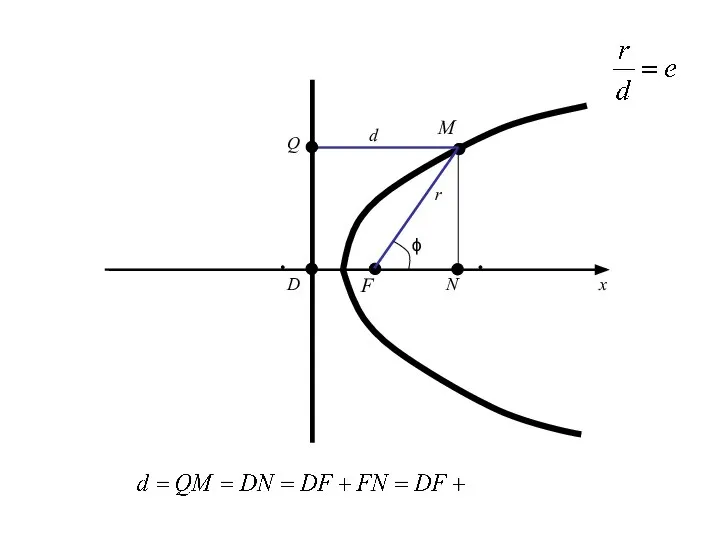
- 108. M F D x r d Q ϕ N
- 109. M F D x r d Q ϕ N
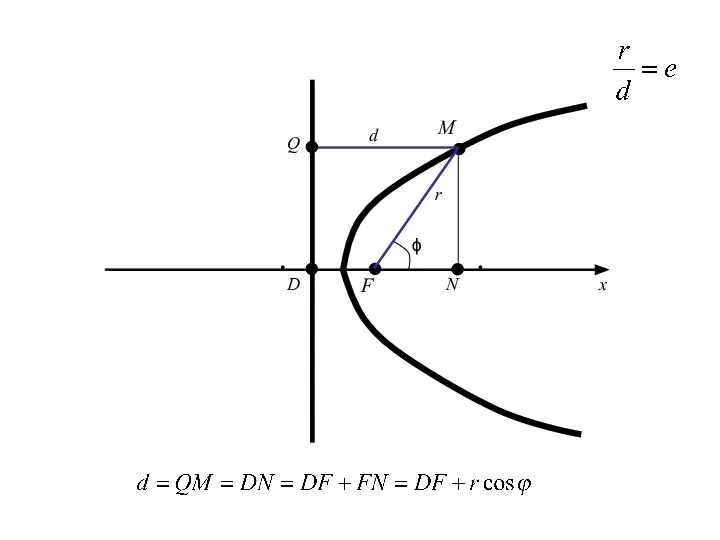
- 110. M F D O x r d Q N ϕ
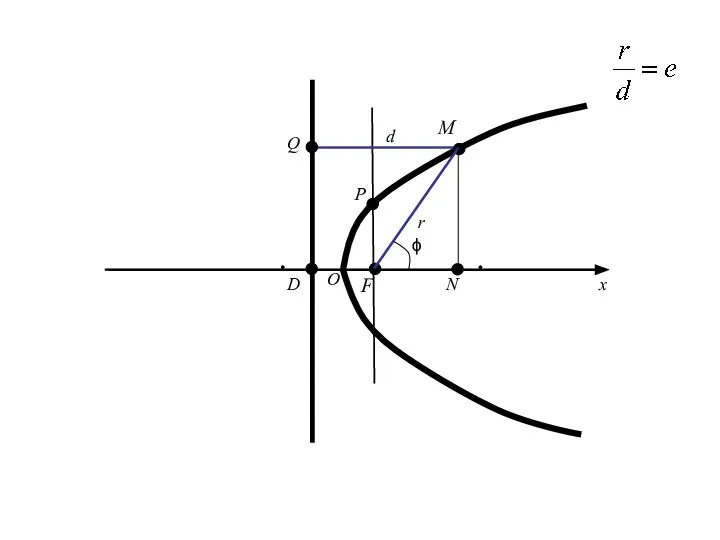
- 111. M F D O x P r d Q N ϕ
- 112. M F D O x P r d S Q N ϕ
- 113. M F D O x P r d S Q N ϕ
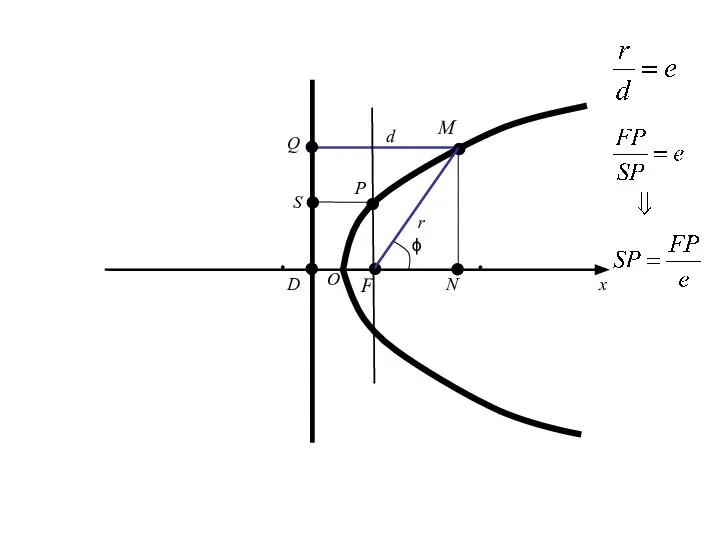
- 114. Половина длины фокальной хорды (т. е. хорды, проходящей через фокус перпендикулярно к фокальной оси) называется фокальным
- 115. Половина длины фокальной хорды (т. е. хорды, проходящей через фокус перпендикулярно к фокальной оси) называется фокальным
- 116. Половина длины фокальной хорды (т. е. хорды, проходящей через фокус перпендикулярно к фокальной оси) называется фокальным
- 117. Половина длины фокальной хорды (т. е. хорды, проходящей через фокус перпендикулярно к фокальной оси) называется фокальным
- 118. Половина длины фокальной хорды (т. е. хорды, проходящей через фокус перпендикулярно к фокальной оси) называется фокальным
- 119. Половина длины фокальной хорды (т. е. хорды, проходящей через фокус перпендикулярно к фокальной оси) называется фокальным
- 120. Половина длины фокальной хорды (т. е. хорды, проходящей через фокус перпендикулярно к фокальной оси) называется фокальным
- 121. Половина длины фокальной хорды (т. е. хорды, проходящей через фокус перпендикулярно к фокальной оси) называется фокальным
- 123. Скачать презентацию
















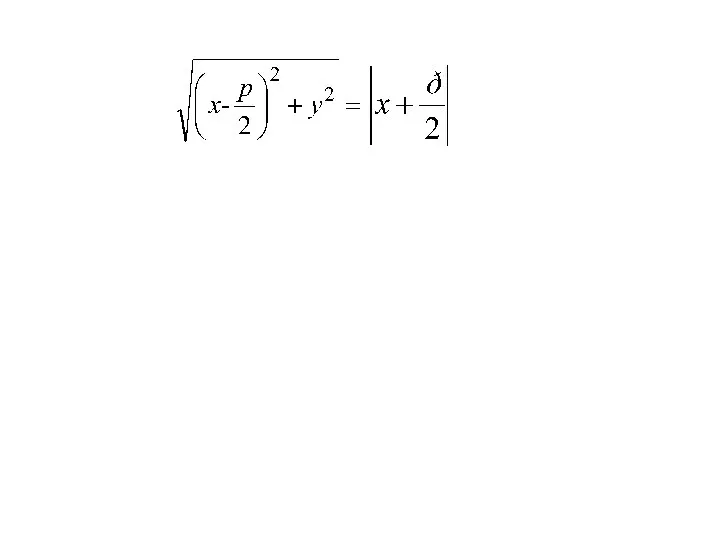
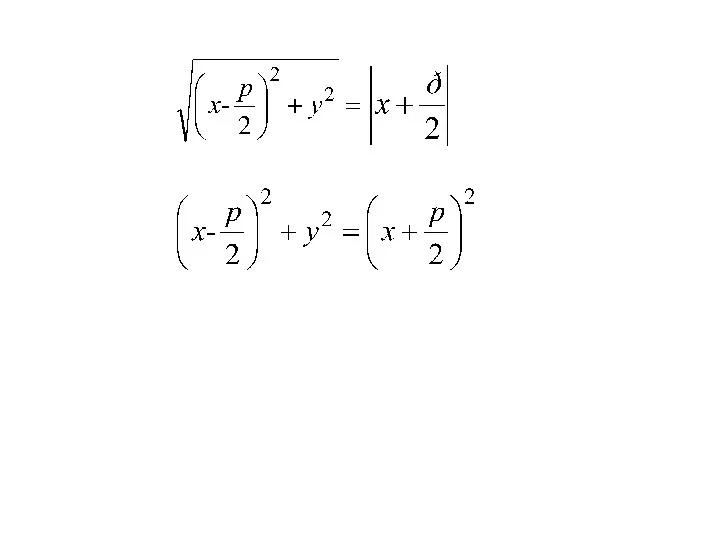
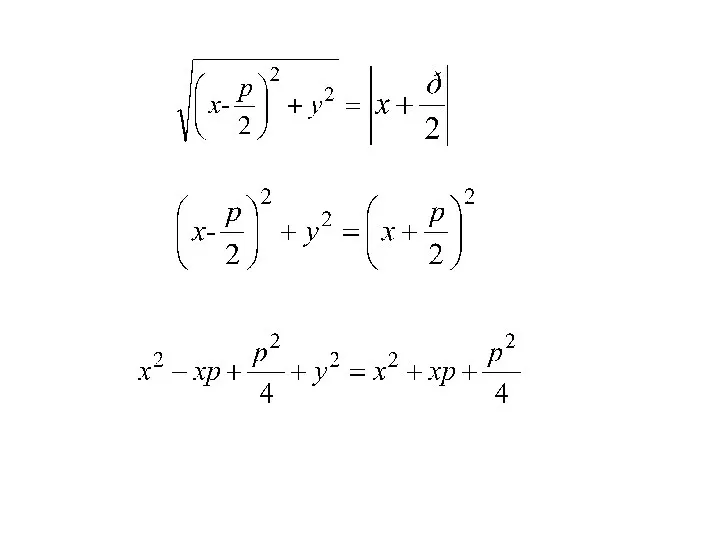
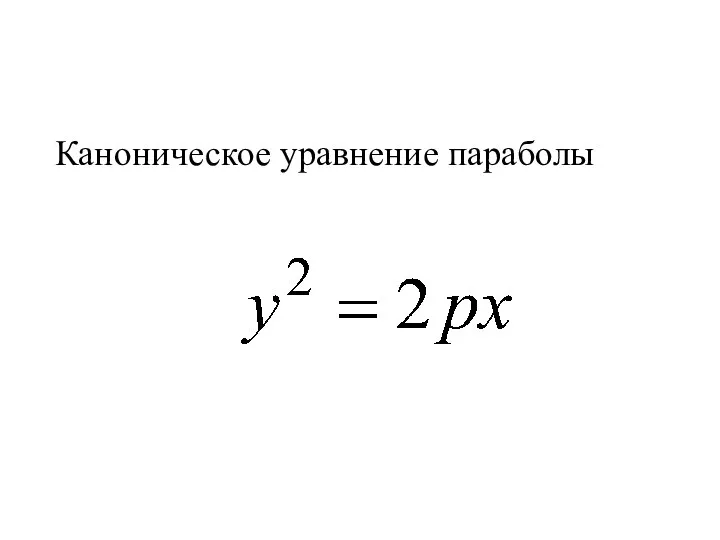








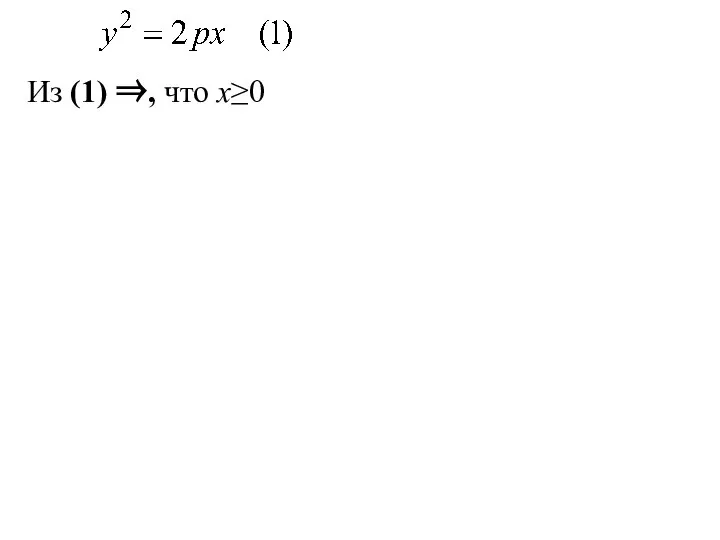
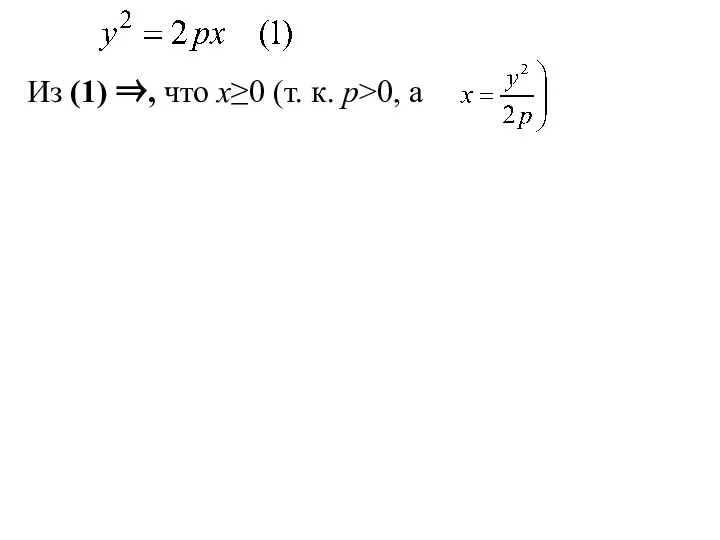





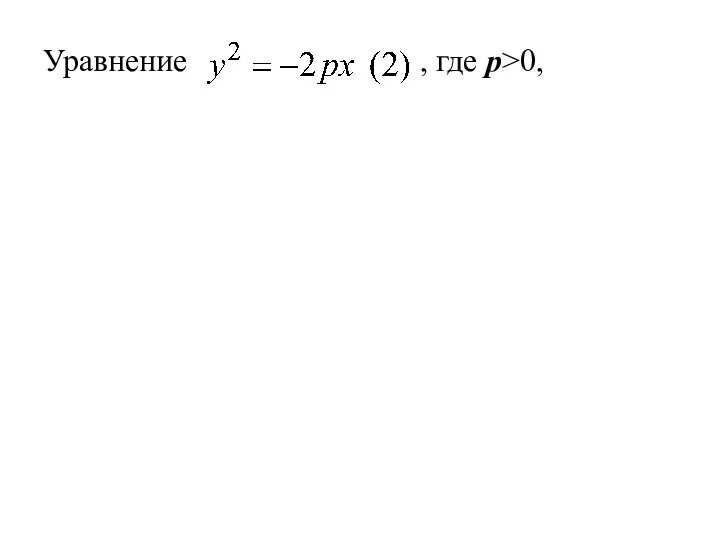




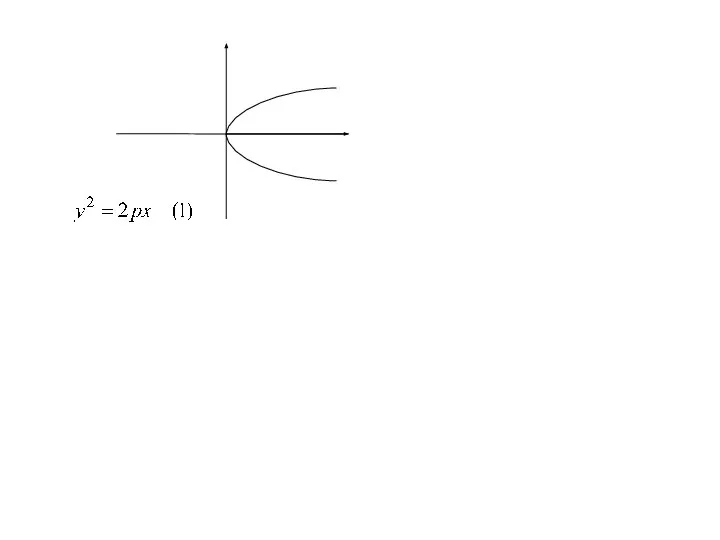
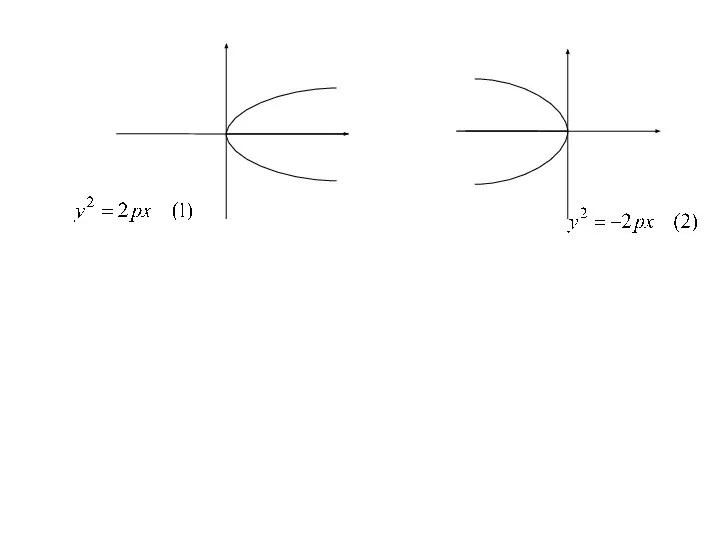
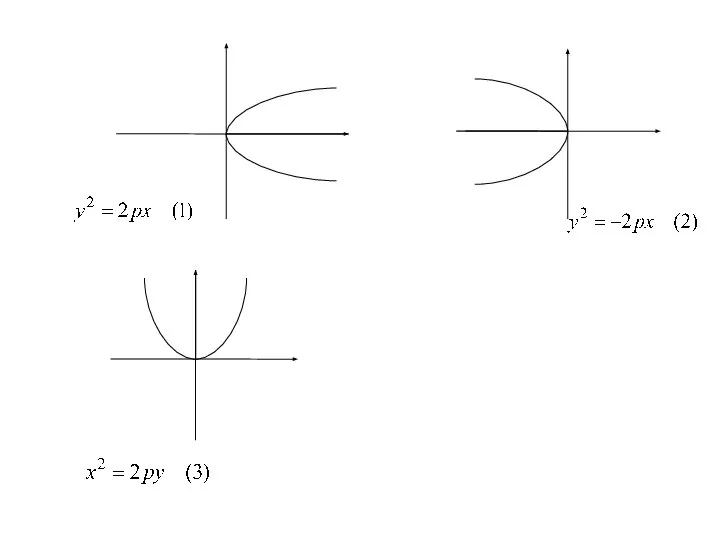
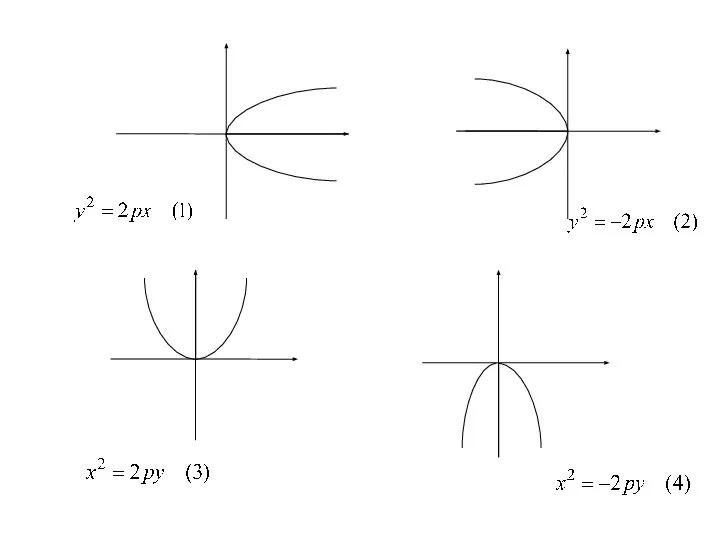




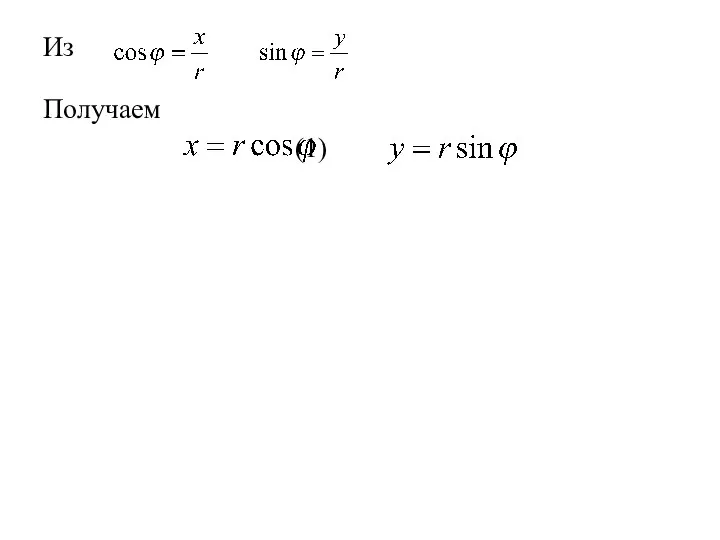







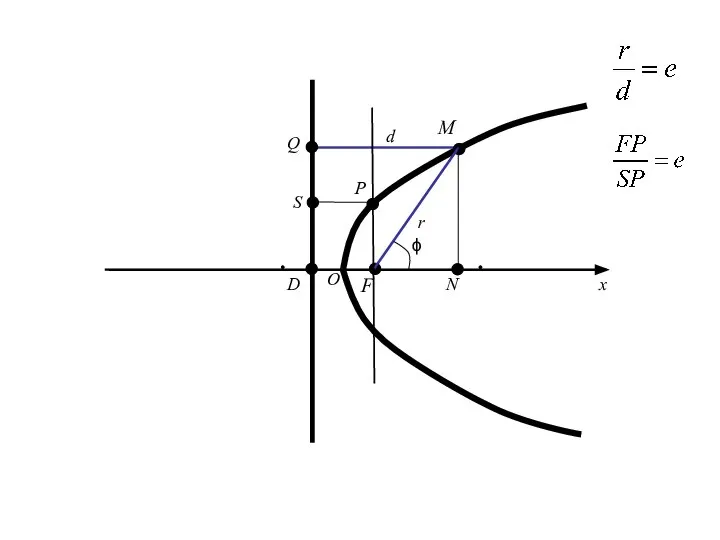








 Стандарты об образовании
Стандарты об образовании Презентация "Особенности английской живописи XIX века" - скачать презентации по МХК
Презентация "Особенности английской живописи XIX века" - скачать презентации по МХК Тренажер.Таблица умножения - презентация для начальной школы
Тренажер.Таблица умножения - презентация для начальной школы Теории лидерства
Теории лидерства Древние образы и символы в народном искусстве.Часть 1
Древние образы и символы в народном искусстве.Часть 1 Применение определенного интеграла Геометрическое приложение. Механическое приложение.
Применение определенного интеграла Геометрическое приложение. Механическое приложение. Методические рекомендации к составлению основной общеобразовательной программы ДОУ компенсирующего вида
Методические рекомендации к составлению основной общеобразовательной программы ДОУ компенсирующего вида Автоматизация анализа текстов партий
Автоматизация анализа текстов партий Дуговая сталеплавильная печь емкостью G=150т
Дуговая сталеплавильная печь емкостью G=150т Лёгкая атлетика
Лёгкая атлетика Культура стран халифата
Культура стран халифата Презентация Порядок назначения на должности государственной гражданской службы таможенных органов
Презентация Порядок назначения на должности государственной гражданской службы таможенных органов Sights of Prague. The dancing house
Sights of Prague. The dancing house Техническое обслуживание и текущий ремонт тележек модели 18-9810
Техническое обслуживание и текущий ремонт тележек модели 18-9810 Православный иконостас
Православный иконостас Легенды о Минске: интерпретация в современном контексте
Легенды о Минске: интерпретация в современном контексте ПИЩЕВЫЕ ОТРАВЛЕНИЯ. ГИГИЕНИЧЕСКИЕ ТРЕБОВАНИЯ К ПИЩЕБЛОКУ. Лекции
ПИЩЕВЫЕ ОТРАВЛЕНИЯ. ГИГИЕНИЧЕСКИЕ ТРЕБОВАНИЯ К ПИЩЕБЛОКУ. Лекции Плоское движение твёрдого тела
Плоское движение твёрдого тела Циклические алгоритмы. Виды циклов и циклические команды на Паскале
Циклические алгоритмы. Виды циклов и циклические команды на Паскале Сетевая модель OSI
Сетевая модель OSI Статистический подход Шеннона
Статистический подход Шеннона  СТРАХОВЫЕ КОМПАНИИ
СТРАХОВЫЕ КОМПАНИИ  Хрящевая и костная ткань
Хрящевая и костная ткань  Организация и методические основы проведения урока физической культуры
Организация и методические основы проведения урока физической культуры  ФОРМИРОВАНИЕ МОДЕЛИ ФУНКЦИОНИРОВАНИЯ ПРОГРАММНОГО СРЕДСТВА С ИСПОЛЬЗОВАНИЕМ UML 2
ФОРМИРОВАНИЕ МОДЕЛИ ФУНКЦИОНИРОВАНИЯ ПРОГРАММНОГО СРЕДСТВА С ИСПОЛЬЗОВАНИЕМ UML 2 3. Солдат и смерть
3. Солдат и смерть Орфографический режим в начальной школе - презентация для начальной школы
Орфографический режим в начальной школе - презентация для начальной школы Счетчики, регистры. (Лекция 7)
Счетчики, регистры. (Лекция 7)