Содержание
- 2. Комплексным числом называется выражение вида а + bi, в котором а и b – действительные числа,
- 3. Два комплексных числа (a; b) и (c; d) называются равными, если а = с и b
- 4. Арифметические операции над комплексными числами Суммой комплексных чисел z = (a; b) и w = (c;
- 5. Справедливо следующее правило: (a; b) – (c; d) = (a – c; b – d). Произведением
- 6. Пример 1 Вычислить: Пример 1 Вычислить:
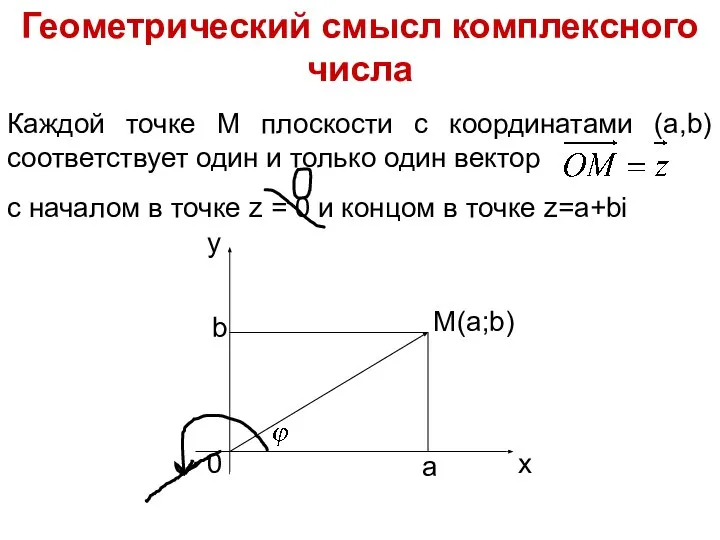
- 7. Геометрический смысл комплексного числа Каждой точке М плоскости с координатами (a,b) соответствует один и только один
- 8. Если комплексное число Z= a+bi трактовать как точку M (a,b) плоскости xOy, то модуль Z равен
- 9. Тригонометрическая форма комплексного числа Тригонометрической формой комплексного числа называют его запись в виде: z = r(cosφ
- 10. Пример2. Записать в тригонометрической форме: Сначала находим модуль числа: Далее, согласно формулам (*), имеем: Учитывая, что
- 11. Действия над комплексными числами, заданными в тригонометрической форме При умножении/делении комплексных чисел, заданных в тригонометрической форме,
- 12. Пример3. Выполнить действия: Используя формулу (1), находим:
- 13. При возведении комплексного числа z = r (Cosφ + iSinφ) в натуральную степень n модуль данного
- 14. Пример4. Решить уравнение Корнями данного уравнения являются все значения Для числа - 4 имеем r =
- 16. Скачать презентацию












 Смотр-конкурс макетов «Прогулочная площадка моей мечты». Ландшафтный дизайн
Смотр-конкурс макетов «Прогулочная площадка моей мечты». Ландшафтный дизайн Неоднозначность факторного решения
Неоднозначность факторного решения Нурбаев
Нурбаев глагол to be
глагол to be Первобытная магия и ритуалы
Первобытная магия и ритуалы Цель: определить влияние педагогического мастерства учителя на качество образования.
Цель: определить влияние педагогического мастерства учителя на качество образования. Презентация Уголовная ответственность несовершеннолетних
Презентация Уголовная ответственность несовершеннолетних Жизненный цикл организации Петрова М. Зедеев А.
Жизненный цикл организации Петрова М. Зедеев А. ПОСТРОЕНИЕ ДИАГРАММ В табличном процессоре Microsoft Excel
ПОСТРОЕНИЕ ДИАГРАММ В табличном процессоре Microsoft Excel Органи державної влади в Україні
Органи державної влади в Україні Стратегическое управление. Лекция 3
Стратегическое управление. Лекция 3 Провідні шляхи головного і спинного мозку, їх класифікація
Провідні шляхи головного і спинного мозку, їх класифікація Работы, выполняемые на авиационной технике
Работы, выполняемые на авиационной технике Основы религиозных культур и светской этики
Основы религиозных культур и светской этики Эволюция либеральной демократии
Эволюция либеральной демократии Разрез «Распадский»
Разрез «Распадский» Расчет на силовое динамическое воздействие во временной области
Расчет на силовое динамическое воздействие во временной области Стандарт изображения объекта розничной торговли SI GEELY AUTO
Стандарт изображения объекта розничной торговли SI GEELY AUTO Гибкие электропередачи
Гибкие электропередачи Олимпийские кольца
Олимпийские кольца Составление маршрута экскурсии
Составление маршрута экскурсии Презентация Судебно-психологическая экспертиза; требования, разновидности.
Презентация Судебно-психологическая экспертиза; требования, разновидности. Структуры в Си-программах. Семантика и синтез
Структуры в Си-программах. Семантика и синтез 2 класс. Учитель: Мастранская Ольга Николаевна.
2 класс. Учитель: Мастранская Ольга Николаевна. Основы C# и события в Unity
Основы C# и события в Unity Алгебра модуля - презентация по Алгебре
Алгебра модуля - презентация по Алгебре Отладочная плата MCS-51
Отладочная плата MCS-51 Программирование на языке MATLAB. Работа с массивами данных
Программирование на языке MATLAB. Работа с массивами данных