Содержание
- 2. Понятие множества Множество - это совокупность определенных различаемых объектов, причем таких, что для каждого можно установить,
- 3. Обычно множества обозначают большими буквами: A,B,X N ,…, а их элементы – соответствующими маленькими буквами: a,b,x,n…
- 4. Множества могут быть конечными, бесконечными и пустыми. Множество, содержащее конечное число элементов, называется конечным. Если множество
- 5. Способы задания множеств Существуют три способа задания множеств: 1) описание множества Примеры: Y={yΙ1≤y ≤10} –множество значений
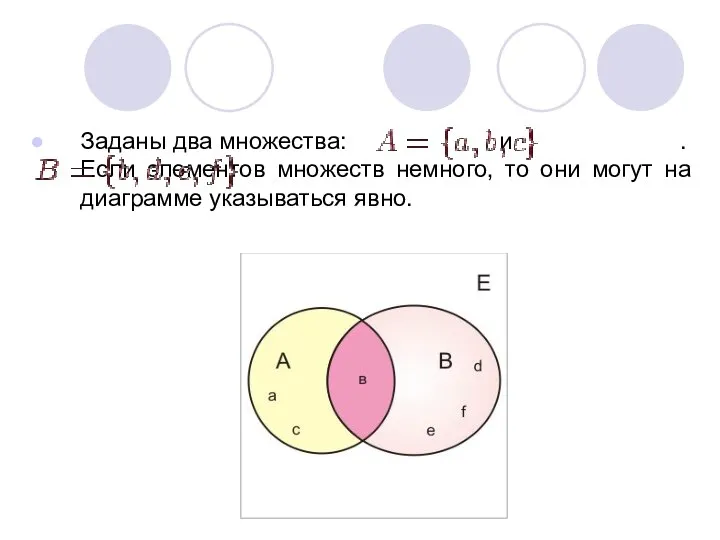
- 6. Заданы два множества: и .Если элементов множеств немного, то они могут на диаграмме указываться явно.
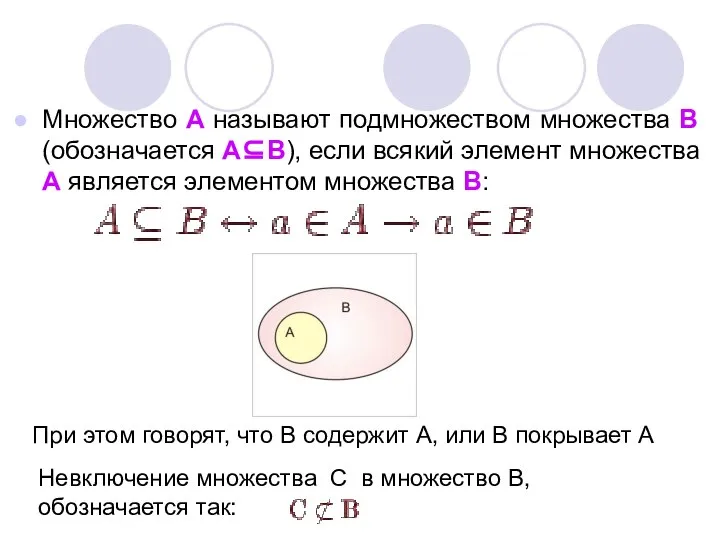
- 7. Множество А называют подмножеством множества В (обозначается А⊆В), если всякий элемент множества А является элементом множества
- 8. Множества А и В равны (А=В) тогда и только тогда, когда , А⊆В и В⊆А ,
- 9. Множество А называется собственным подмножеством множества В, если А⊆В, а В⊄А. Обозначается так: А⊂В. Например, Принято
- 10. Операции над множествами Объединением (суммой) множеств А и В (обозначается А∪В) называется множество С тех элементов,
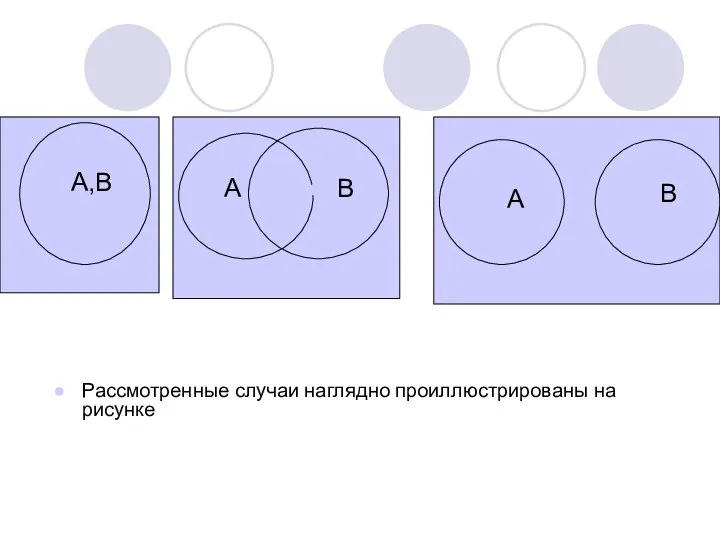
- 11. Рассмотренные случаи наглядно проиллюстрированы на рисунке А,В А В А В
- 12. Пересечением множеств А и В называется новое множество С, которое состоит только из элементов одновременно принадлежащих,
- 13. Примеры: 1)А={1,2,3}, B= {1,2,3}, тогда А∩В= {1,2,3}. 2)А={1,2,3}, B={2,3,4,5,6}, тогда А∩В={2,3} 3) A={1,2,3}, B={4,6,8}, тогда А∩В=∅
- 14. Разностью множеств А и В называется множество С, состоящее из элементов принадлежащих только множеству А и
- 15. Даны два множества: А={1,2,3,b,c,d},В={2,b,d,3}. Тогда: A∪B={1,2,3,b,c,d} B подмножество А А\В={1,c} A∩B={2,3,b,d}
- 16. Свойства: 1. Коммутативность объединения А∪B=B ∪ A 2. Коммутативность пересечения А ∩ В=В ∩ А 3.
- 17. Декартовое (прямое) произведение А и В - это новое множество С, состоящее из упорядоченных пар, в
- 19. Скачать презентацию













 Основы проектирования производственных зданий
Основы проектирования производственных зданий Презентация "Преобразование системы «Научного менеджмента» Ф. У. Тейлора" - скачать презентации по Экономике
Презентация "Преобразование системы «Научного менеджмента» Ф. У. Тейлора" - скачать презентации по Экономике Операторское искусство и монтаж. Мастер-класс
Операторское искусство и монтаж. Мастер-класс Тихая моя Родина - презентация для начальной школы_
Тихая моя Родина - презентация для начальной школы_ Рождество Христово
Рождество Христово Цветоведение
Цветоведение  Лого Титульный слайд Лого Титульный слайд Слайд содержание (1) Тексты, (слева)преобразованные в графический файл.png (transparent-прозрачн
Лого Титульный слайд Лого Титульный слайд Слайд содержание (1) Тексты, (слева)преобразованные в графический файл.png (transparent-прозрачн 27.05.2011 Как сэкономить на полиграфии? Практические советы и рекомендации Дни Директ маркетинга в Украине 2011. Competence Day 27.05.2011 Сергей Сн
27.05.2011 Как сэкономить на полиграфии? Практические советы и рекомендации Дни Директ маркетинга в Украине 2011. Competence Day 27.05.2011 Сергей Сн Ашық сабақ. Акробатикалық жаттығулардың
Ашық сабақ. Акробатикалық жаттығулардың Основы информационного права
Основы информационного права Реабилитация. Возмещение вреда
Реабилитация. Возмещение вреда Национальные символы Великобритании
Национальные символы Великобритании Ференц Лист Выполнила Иванова Мария
Ференц Лист Выполнила Иванова Мария my-morning-routine-before-going-to-school-activities-promoting-classroom-dynamics-group-form_8652
my-morning-routine-before-going-to-school-activities-promoting-classroom-dynamics-group-form_8652 Разработка элементов системы менеджмента качества для ресторана «неГорький сад» в городе Ижевск
Разработка элементов системы менеджмента качества для ресторана «неГорький сад» в городе Ижевск Мобильная медицина, как компонент реализации концепции модернизации и информатизации системы здравоохранения России Мавлю
Мобильная медицина, как компонент реализации концепции модернизации и информатизации системы здравоохранения России Мавлю Процесс и артефакты mardovich.blogspot.com
Процесс и артефакты mardovich.blogspot.com Закон об энергосбережении и о повышении энергетической эффективности и о внесении изменений в отдельные законодательные акты
Закон об энергосбережении и о повышении энергетической эффективности и о внесении изменений в отдельные законодательные акты Бібліотека Компас-Shaft 2D. Створення кресленика вала
Бібліотека Компас-Shaft 2D. Створення кресленика вала Рашит Мухаметбареевич Нурмухаметов (1925–1986)
Рашит Мухаметбареевич Нурмухаметов (1925–1986)  Исламские просветители
Исламские просветители Подходы к определению понятия "умственная отсталость"
Подходы к определению понятия "умственная отсталость" Приказное производство. Понятие и особенности судебного приказа
Приказное производство. Понятие и особенности судебного приказа «Что говорят ваши клиенты сегодня?»
«Что говорят ваши клиенты сегодня?» ВСТРЕЧА С БОГОМ Цель урока: Изучение видеоряда, изображающего различные культовые здания: античные, индийские, египетские, бу
ВСТРЕЧА С БОГОМ Цель урока: Изучение видеоряда, изображающего различные культовые здания: античные, индийские, египетские, бу Технология Superpave, как инновационный метод проектирования асфальтобетонных смесей
Технология Superpave, как инновационный метод проектирования асфальтобетонных смесей Италия. Конституция Итальянской Республики
Италия. Конституция Итальянской Республики Правовой статус общества с ограниченной ответственностью "Smolnygroup"
Правовой статус общества с ограниченной ответственностью "Smolnygroup"