Содержание
- 2. 28.04.2014 Кратчайшие пути 1 Кратчайшие пути в графе Путь p в графе G = (V, E):
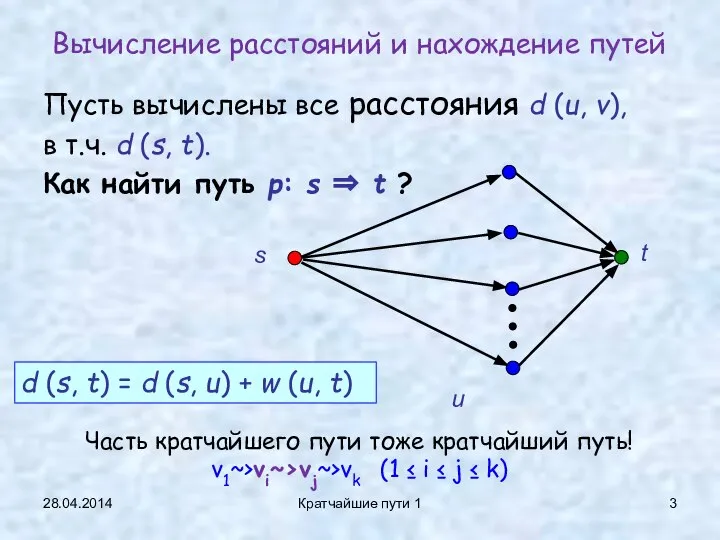
- 3. 28.04.2014 Кратчайшие пути 1 Вычисление расстояний и нахождение путей Пусть вычислены все расстояния d (u, v),
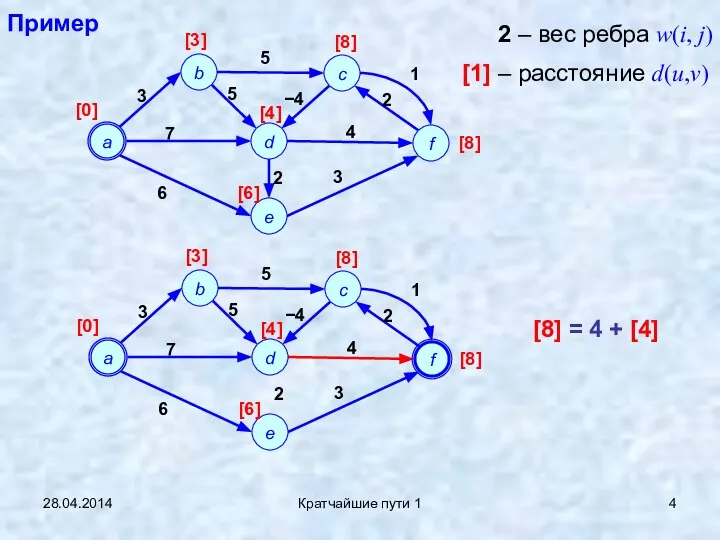
- 4. 28.04.2014 Кратчайшие пути 1 Пример 2 – вес ребра w(i, j) [1] – расстояние d(u,v) [8]
- 5. 28.04.2014 Кратчайшие пути 1 Пример [4] = − 4 + [8] [8] = 5 + [3]
- 6. 28.04.2014 Кратчайшие пути 1 Алгоритм нахождения кратчайшего пути по расстояниям между вершинами /*Дано: s, t –
- 7. 28.04.2014 Кратчайшие пути 1 Алгоритм нахождения кратчайшего пути продолжение Детализация строки u = вершина, для которой
- 8. 28.04.2014 Кратчайшие пути 1 Задачи вычисления длин кратчайших путей (расстояний) Стартовая вершина s фиксирована, конечная вершина
- 9. 28.04.2014 Кратчайшие пути 1 Задачи вычисления расстояний от фиксированной вершины Общая схема большинства алгоритмов: рассматриваются временные
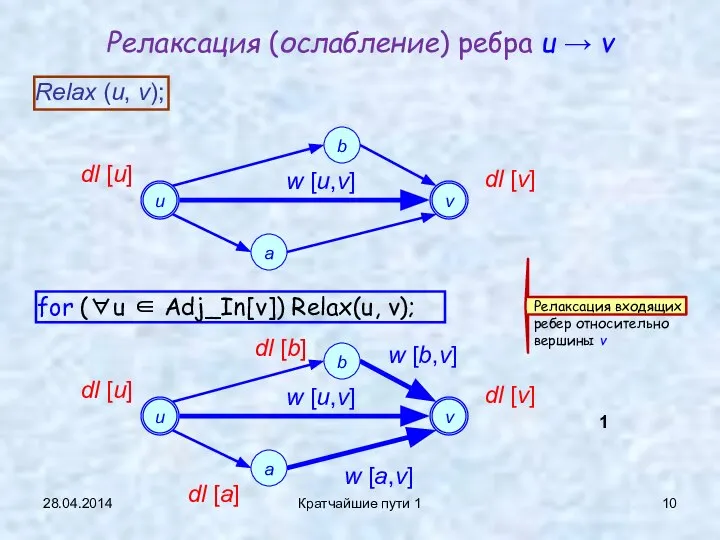
- 10. 28.04.2014 Кратчайшие пути 1 Релаксация (ослабление) ребра u → v 1 dl [u] dl [v] w
- 11. 28.04.2014 Кратчайшие пути 1 Релаксация входящих ребер относительно вершины v : for (∀u ∈ Adj_In[v]) Relax(u,
- 12. Продолжение на лекции 5 мая 28.04.2014 Кратчайшие пути 1
- 13. 28.04.2014 Кратчайшие пути 1
- 14. Алгоритм Дейкстры (Dijkstra E.W. - 1959) 28.04.2014 Кратчайшие пути 1
- 15. 28.04.2014 Кратчайшие пути 1 Алгоритм Дейкстры W [ *, * ] ≥ 0 Идея алгоритма: V
- 16. 28.04.2014 Кратчайшие пути 1 for (∀ v ∈V) DL[v] =W[s,v]; DL[s] =0; T = V \
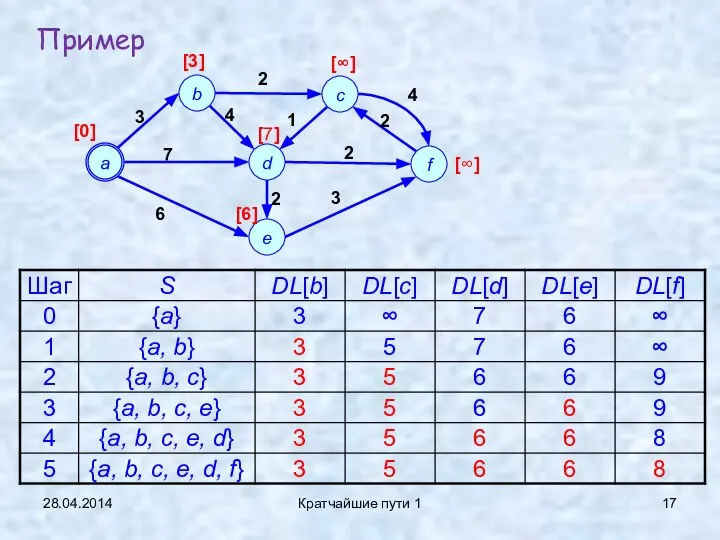
- 17. 28.04.2014 Кратчайшие пути 1 Пример
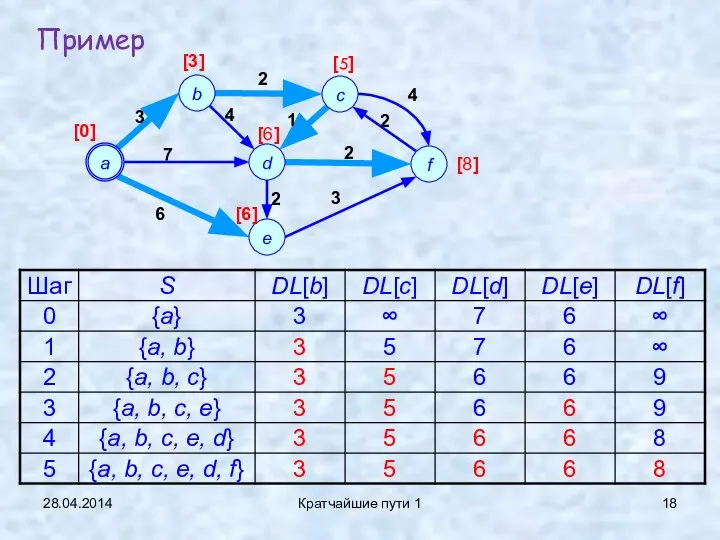
- 18. 28.04.2014 Кратчайшие пути 1 Пример
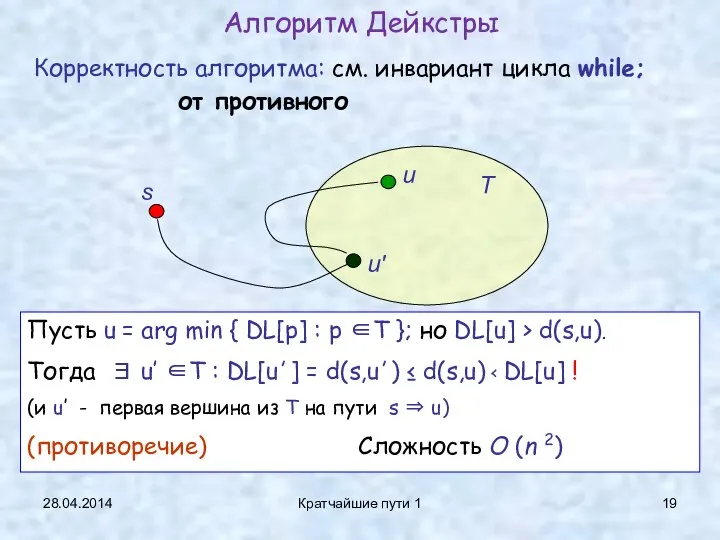
- 19. 28.04.2014 Кратчайшие пути 1 Корректность алгоритма: см. инвариант цикла while; от противного Алгоритм Дейкстры T s
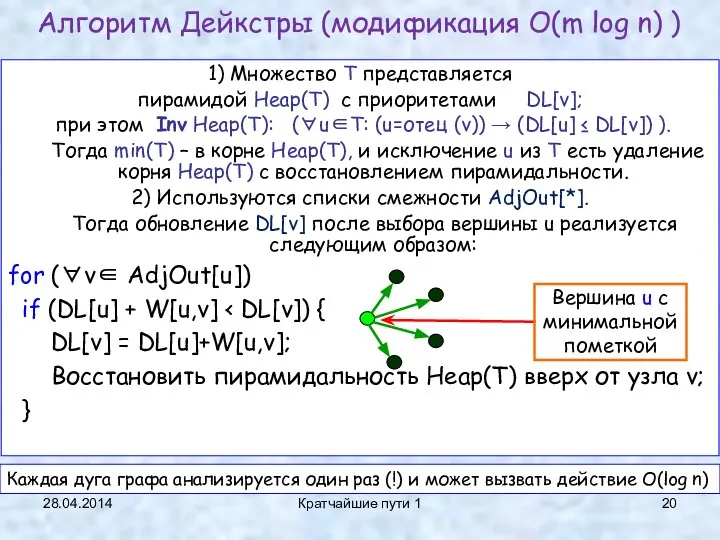
- 20. 28.04.2014 Кратчайшие пути 1 1) Множество T представляется пирамидой Heap(T) с приоритетами DL[v]; при этом Inv
- 21. Следующий Алгоритм Форда-Беллмана 28.04.2014 Кратчайшие пути 1
- 22. 28.04.2014 Кратчайшие пути 1 Алгоритм Форда-Беллмана нахождения расстояний от источника до остальных вершин в графе, не
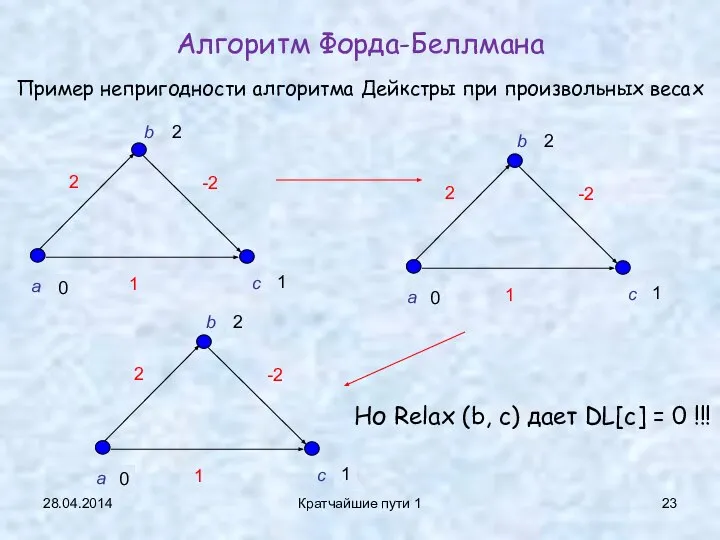
- 23. 0 28.04.2014 Кратчайшие пути 1 Алгоритм Форда-Беллмана Пример непригодности алгоритма Дейкстры при произвольных весах b 2
- 24. 28.04.2014 Кратчайшие пути 1 for (∀ v ∈ V) DL[v] =W[s,v]; DL[s] = 0; for (k=1;
- 25. 28.04.2014 Кратчайшие пути 1 Вариант сложности O (nm) for (∀ v ∈ V) DL[v]=W[s,v]; DL[s] =0;
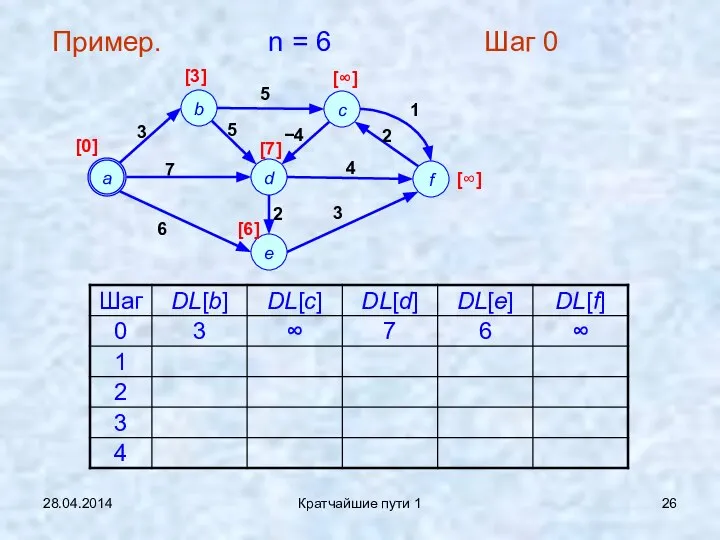
- 26. 28.04.2014 Кратчайшие пути 1 Пример. n = 6 Шаг 0
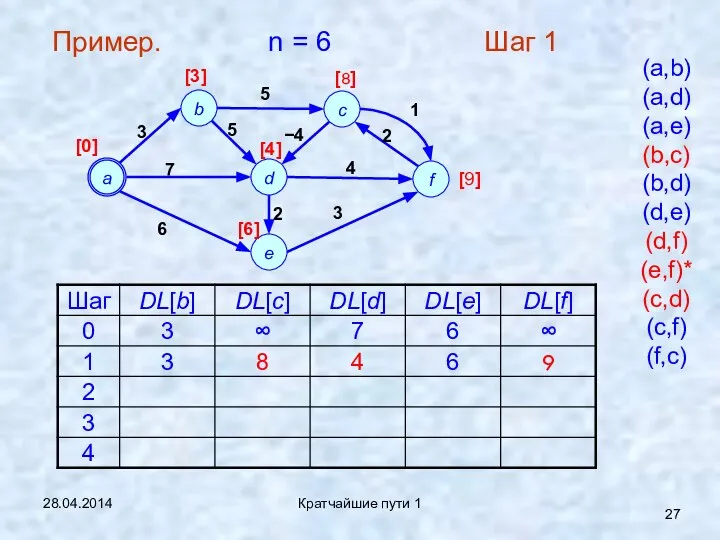
- 27. 28.04.2014 Кратчайшие пути 1 Пример. n = 6 Шаг 1 (a,b) (a,d) (a,e) (b,c) (b,d) (d,e)
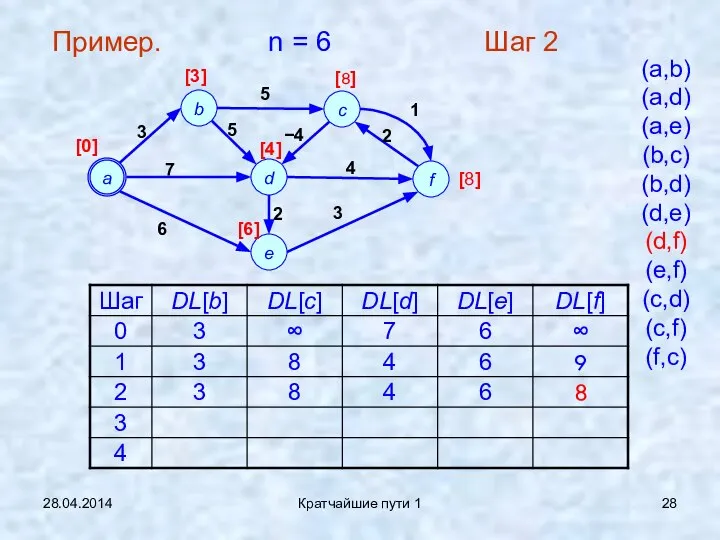
- 28. 28.04.2014 Кратчайшие пути 1 Пример. n = 6 Шаг 2 (a,b) (a,d) (a,e) (b,c) (b,d) (d,e)
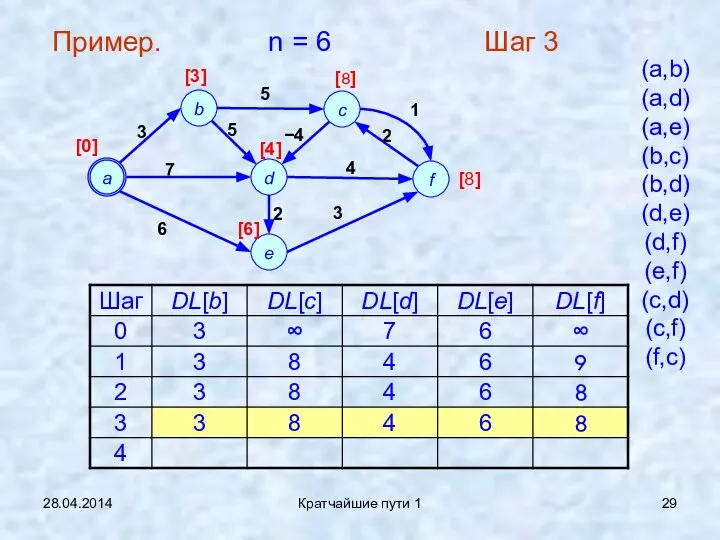
- 29. 28.04.2014 Кратчайшие пути 1 Пример. n = 6 Шаг 3 (a,b) (a,d) (a,e) (b,c) (b,d) (d,e)
- 30. 28.04.2014 Кратчайшие пути 1 Индуктивное утверждение (“инвариант”) цикла for (k=1; k P( [1..k) ) ≡ (
- 31. 28.04.2014 Кратчайшие пути 1 Если P( [1..k) ) и P( [1..k] ) действительно инварианты, то для
- 32. 28.04.2014 Кратчайшие пути 1 После очередной итерации d(s,v) ≤ DL[v] ≤ { по алгоритму, с учетом
- 33. 28.04.2014 Кратчайшие пути 1 Кратчайшие пути между всеми парами вершин См. лекцию 12
- 34. Примечание 28.04.2014 Кратчайшие пути 1
- 36. Скачать презентацию

![28.04.2014 Кратчайшие пути 1 Пример [4] = − 4 + [8]](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/1301917/slide-4.jpg)






![28.04.2014 Кратчайшие пути 1 Алгоритм Дейкстры W [ *, * ]](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/1301917/slide-14.jpg)
![28.04.2014 Кратчайшие пути 1 for (∀ v ∈V) DL[v] =W[s,v]; DL[s]](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/1301917/slide-15.jpg)


![28.04.2014 Кратчайшие пути 1 for (∀ v ∈ V) DL[v] =W[s,v];](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/1301917/slide-23.jpg)


![28.04.2014 Кратчайшие пути 1 Если P( [1..k) ) и P( [1..k]](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/1301917/slide-30.jpg)
![28.04.2014 Кратчайшие пути 1 После очередной итерации d(s,v) ≤ DL[v] ≤](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/1301917/slide-31.jpg)


 Викторина по творчеству и биографии Антона Павловича Чехова - презентация для начальной школы_
Викторина по творчеству и биографии Антона Павловича Чехова - презентация для начальной школы_ Человек и профессия
Человек и профессия Критерии успешности учителя, воспитателя
Критерии успешности учителя, воспитателя 21 нче февраль – Халыкара туган тел көне
21 нче февраль – Халыкара туган тел көне Функции по защите информации руководителя предприятия
Функции по защите информации руководителя предприятия Features that are available only in the Advanced version: 3D simulation
Features that are available only in the Advanced version: 3D simulation Презентация "Инвестиции муниципального образования" - скачать презентации по Экономике
Презентация "Инвестиции муниципального образования" - скачать презентации по Экономике Архитектура. Разновидности форм кровли. Учитель ИЗО,МОСШ№3, г. Белоярский, ХМАО Шаньшерова М.М.
Архитектура. Разновидности форм кровли. Учитель ИЗО,МОСШ№3, г. Белоярский, ХМАО Шаньшерова М.М. ПОДГОТОВКА К СЕРТИФИКАЦИОННОМУ АУДИТУ Евгения Соловей Сибирский сертификационный центр
ПОДГОТОВКА К СЕРТИФИКАЦИОННОМУ АУДИТУ Евгения Соловей Сибирский сертификационный центр  Неоинституциональная экономическая теория К.э.н., ст. препод. Бренделева Елена Алексеевна
Неоинституциональная экономическая теория К.э.н., ст. препод. Бренделева Елена Алексеевна  Региональные туристские организации
Региональные туристские организации Back-end. Протокол HTTP
Back-end. Протокол HTTP Чертежи фасадов зданий. Последовательность вычерчивания фасада здания. Наименование фасадов здания на чертеже
Чертежи фасадов зданий. Последовательность вычерчивания фасада здания. Наименование фасадов здания на чертеже Индуизм. Тилака или тилак. Теория и практика
Индуизм. Тилака или тилак. Теория и практика Развитие скоростно-силовых способностей юных волейболистов
Развитие скоростно-силовых способностей юных волейболистов Презентация Экологические права граждан и общественных объединений
Презентация Экологические права граждан и общественных объединений  Скрининг состояния организма за 5 минут с DePuls+
Скрининг состояния организма за 5 минут с DePuls+ Золотое сечение. Научно-практическая конфереция
Золотое сечение. Научно-практическая конфереция Работы победителей муниципального этапа областного конкурса детского и юношеского изобразительного искусства «Я рисую
Работы победителей муниципального этапа областного конкурса детского и юношеского изобразительного искусства «Я рисую Конфликты в школе
Конфликты в школе «Методы повышения учебной мотивации учащихся, развитие познавательной активности учащихся»
«Методы повышения учебной мотивации учащихся, развитие познавательной активности учащихся» Табакерка
Табакерка Хабар агенттіг
Хабар агенттіг телестудия LEONARUS
телестудия LEONARUS  Введение
Введение Поиск информации в сети интернет. Адресная строка
Поиск информации в сети интернет. Адресная строка Логические основы ЭВМ
Логические основы ЭВМ Распознаватели регулярных языков
Распознаватели регулярных языков