Содержание
- 2. 07.05.2013 Кратчайшие пути 2 Расстояния между всеми парами вершин Найти расстояния d(s, t) : ∀ s,
- 3. 07.05.2013 Кратчайшие пути 2 Часть 1 лекции. Вспомогательная тема: Транзитивное замыкание графа. Алгоритм Уоршалла (Warshall) Задан
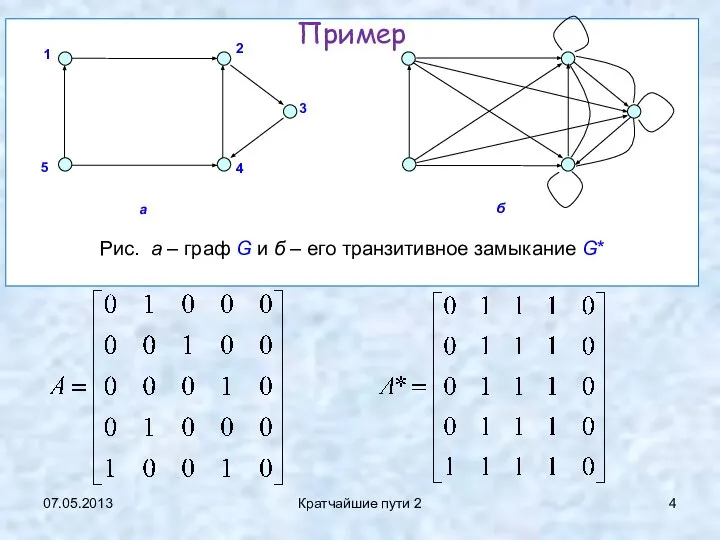
- 4. 07.05.2013 Кратчайшие пути 2 Пример
- 5. 07.05.2013 Кратчайшие пути 2 Матрица путей Матрица путей (или матрица достижимости) P графа G : pij
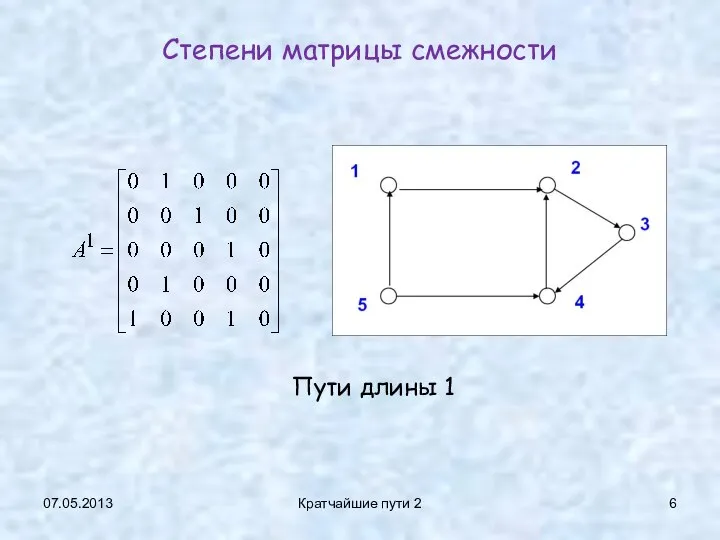
- 6. 07.05.2013 Кратчайшие пути 2 Степени матрицы смежности Пути длины 1
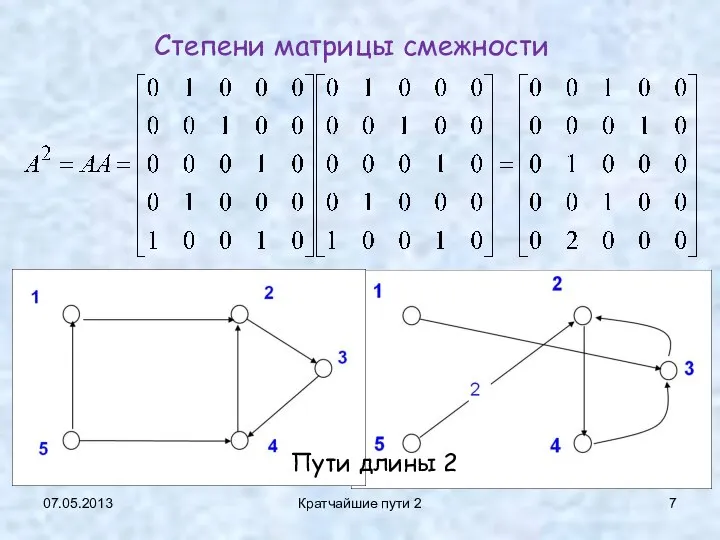
- 7. 07.05.2013 Кратчайшие пути 2 Степени матрицы смежности Пути длины 2
- 8. 07.05.2013 Кратчайшие пути 2 Утверждение. Пусть A есть матрица смежности графа G. Элемент матрицы Ak равен
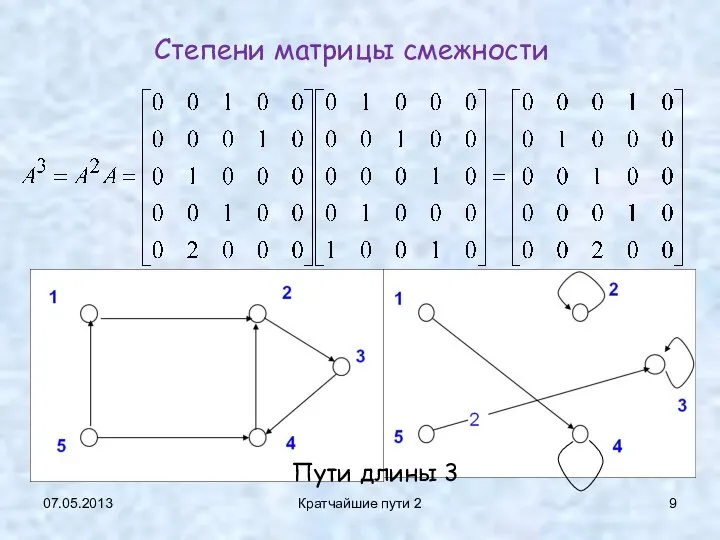
- 9. 07.05.2013 Кратчайшие пути 2 Степени матрицы смежности Пути длины 3
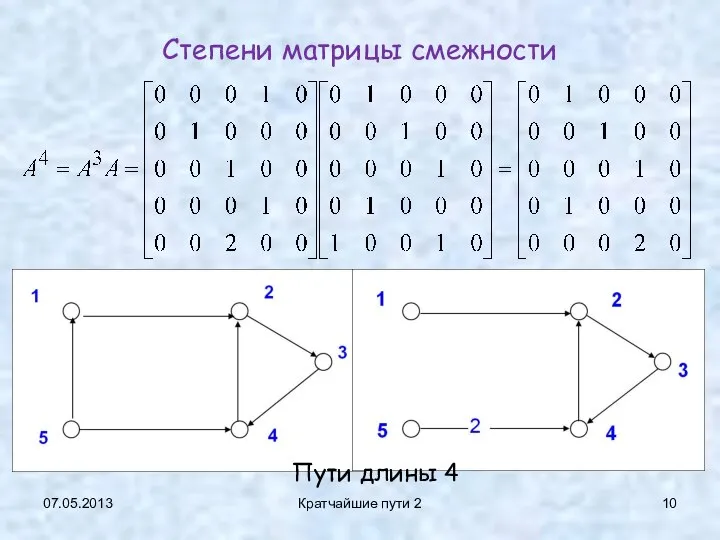
- 10. 07.05.2013 Кратчайшие пути 2 Степени матрицы смежности Пути длины 4
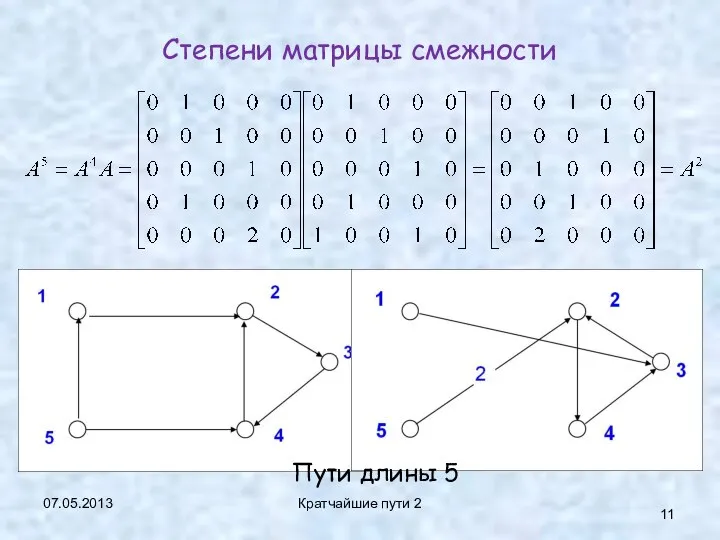
- 11. 07.05.2013 Кратчайшие пути 2 Степени матрицы смежности Пути длины 5
- 12. 07.05.2013 Кратчайшие пути 2 Степени матрицы смежности Т.к. перемножение матриц осуществляется за время O(n3), то вычислить
- 13. 07.05.2013 Кратчайшие пути 2 Определение операции умножения и сложения булевских матриц O(n3log n),
- 14. 07.05.2013 Кратчайшие пути 2 Далее Алгоритм Уоршалла (Warshall) См. далее текстовый файл «Лекция 12 Кратч пути
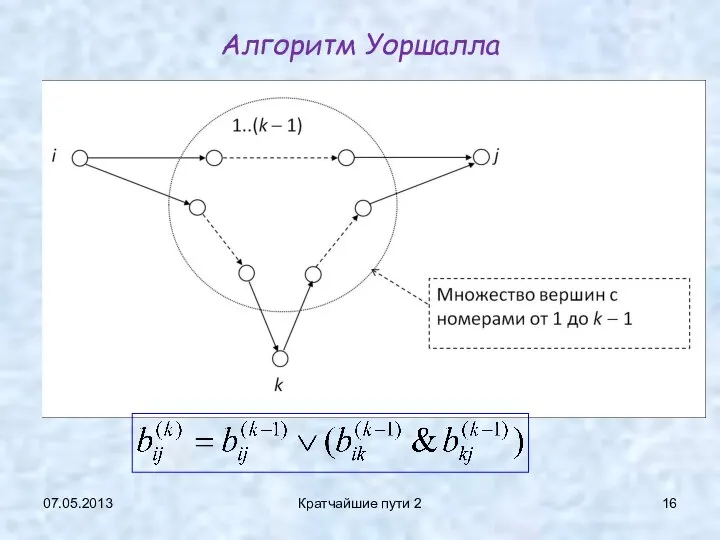
- 15. Алгоритм Уоршалла (Warshall) Пусть вершины графа пронумерованы числами от 1 до n. Нас будут интересовать пути,
- 16. Алгоритм Уоршалла 07.05.2013 Кратчайшие пути 2
- 17. {Инициализация: } {1} for i := 1 to n do {2} for j := 1 to
- 19. Скачать презентацию









 Экономический анализ. Оценка результатов хозяйственной деятельности
Экономический анализ. Оценка результатов хозяйственной деятельности Наркозно-дихальний апарат «ОБЕРІГ»-302 Твій професійний вибір
Наркозно-дихальний апарат «ОБЕРІГ»-302 Твій професійний вибір Айвазовский Иван Константинович
Айвазовский Иван Константинович Merry Christmas!
Merry Christmas! Достижения правоведов и отраслевых психологов в исследованиях преступных групп Подготовила Ивкина Юлия
Достижения правоведов и отраслевых психологов в исследованиях преступных групп Подготовила Ивкина Юлия  Дорога без опасности - презентация для начальной школы
Дорога без опасности - презентация для начальной школы Археология энеолита
Археология энеолита Презентация на тему "Из опыта работы муниципальной системы оценки качества образования" - скачать презентации по Педагогике
Презентация на тему "Из опыта работы муниципальной системы оценки качества образования" - скачать презентации по Педагогике Абсентеизм
Абсентеизм Учебник из семейной библиотеки Проект учащегося 2б класса МОУ СОШ № 17 Зозуля Егора.
Учебник из семейной библиотеки Проект учащегося 2б класса МОУ СОШ № 17 Зозуля Егора. Программирование и разработка веб-приложений. Использование Python для работы с базой данных
Программирование и разработка веб-приложений. Использование Python для работы с базой данных Строительство египетских пирамид
Строительство египетских пирамид Прославление Христа
Прославление Христа Методы обучения
Методы обучения Расчет железобетонных элементов по раскрытию трещин
Расчет железобетонных элементов по раскрытию трещин Особенности и классификация спортивных споров
Особенности и классификация спортивных споров Растениеводство Подготовили: Долиденко Вячеслав
Растениеводство Подготовили: Долиденко Вячеслав Презентация для Мастеров 03.02.2010
Презентация для Мастеров 03.02.2010 Презентация Основные формы собственности на использование вод
Презентация Основные формы собственности на использование вод Возможности использования ИКТ на уроках географии Гикал Людмила Владимировна, учитель географии ГОУ ЦО №1473 имени Г.А Тарана, ЗА
Возможности использования ИКТ на уроках географии Гикал Людмила Владимировна, учитель географии ГОУ ЦО №1473 имени Г.А Тарана, ЗА Натюрморт Мертвая натура?
Натюрморт Мертвая натура? Производная и ее геометрический смысл - презентация по Алгебре
Производная и ее геометрический смысл - презентация по Алгебре Система питания дизеля COMMON RAIL
Система питания дизеля COMMON RAIL Культура России 17 века
Культура России 17 века Тема лекции: Противодиабетические средства Доцент кафедры общей и клинической фармакологии с курсом ФПК и ПК Владимир Михайл
Тема лекции: Противодиабетические средства Доцент кафедры общей и клинической фармакологии с курсом ФПК и ПК Владимир Михайл fb728085_lektsiya_st1.ppt
fb728085_lektsiya_st1.ppt Русский народный праздничный костюм. 5 класс
Русский народный праздничный костюм. 5 класс Научно-практическая конференция «Первые шаги в науку» Тема выступления: «Азбука животного мира родного края»
Научно-практическая конференция «Первые шаги в науку» Тема выступления: «Азбука животного мира родного края»