Содержание
- 2. Булева алгебра Двоичное кодирование – все виды информации кодируются с помощью 0 и 1. Задача –
- 3. Логические высказывания Логическое высказывание – это повествовательное предложение, относительно которого можно однозначно сказать, истинно оно или
- 4. Обозначение высказываний A – Сейчас идет дождь. B – Форточка открыта. простые высказывания (элементарные) Составные высказывания
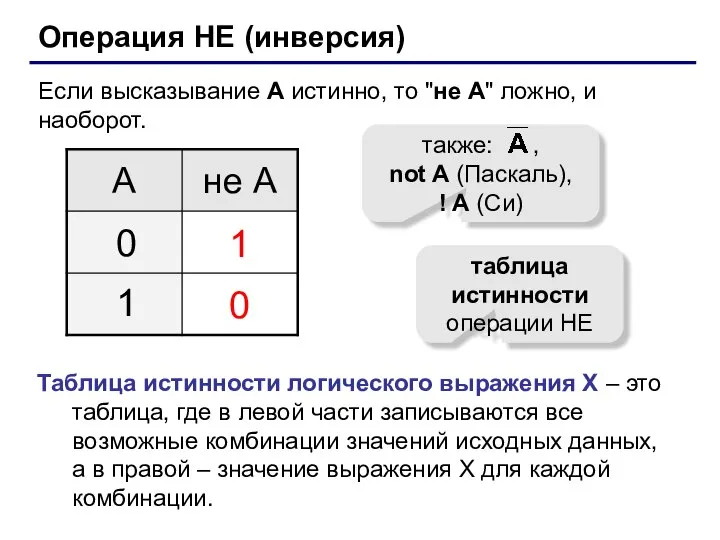
- 5. Операция НЕ (инверсия) Если высказывание A истинно, то "не А" ложно, и наоборот. 1 0 0
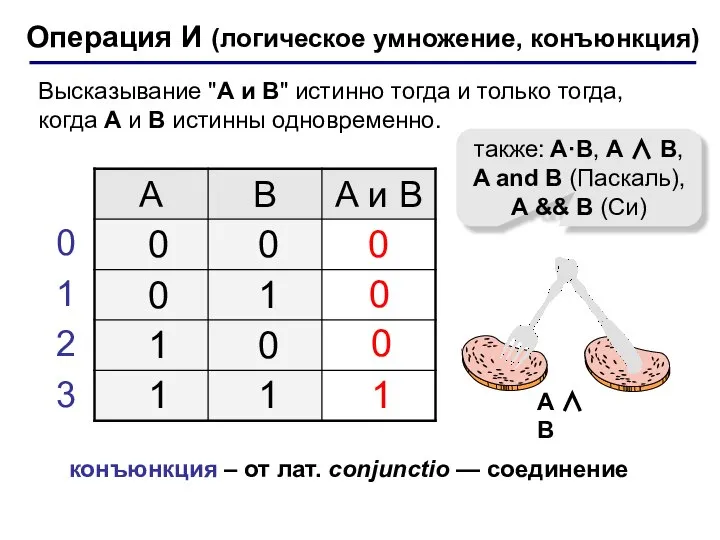
- 6. Операция И (логическое умножение, конъюнкция) 1 0 также: A·B, A ∧ B, A and B (Паскаль),
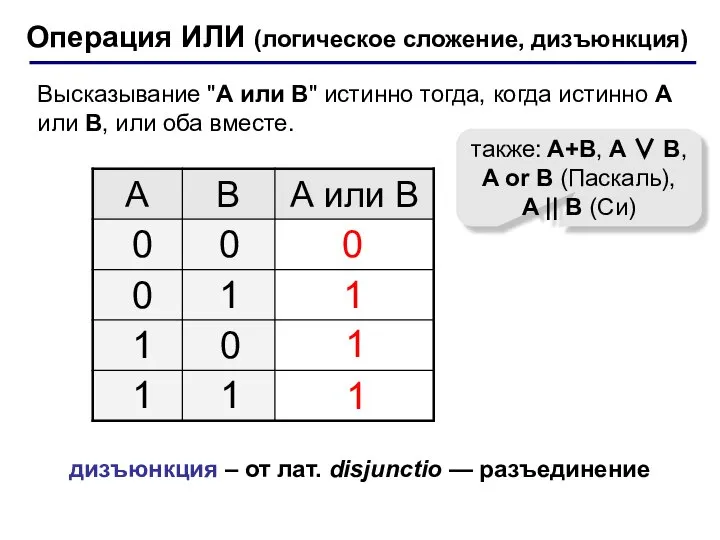
- 7. Операция ИЛИ (логическое сложение, дизъюнкция) 1 0 также: A+B, A ∨ B, A or B (Паскаль),
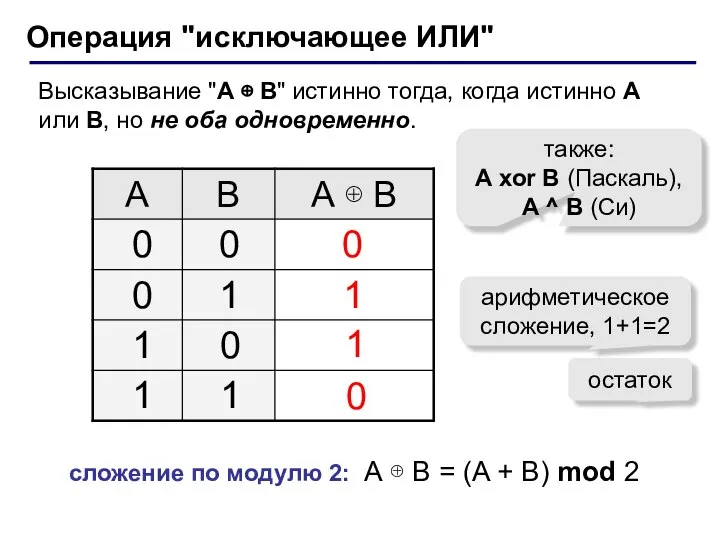
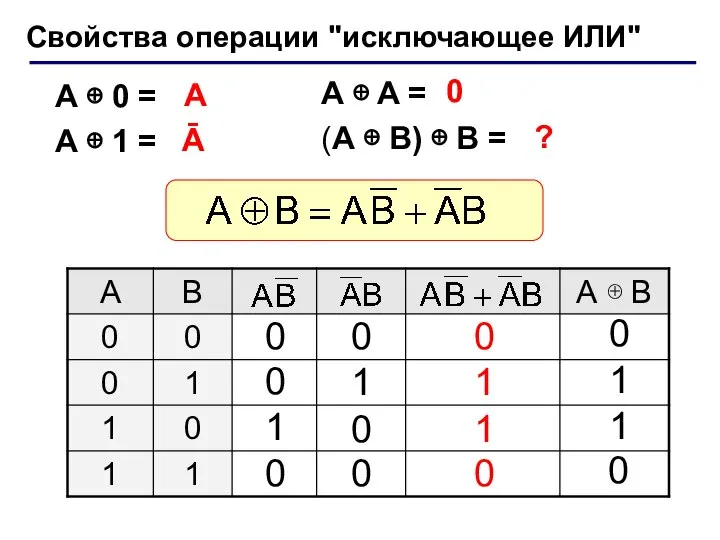
- 8. Операция "исключающее ИЛИ" Высказывание "A ⊕ B" истинно тогда, когда истинно А или B, но не
- 9. A ⊕ A = (A ⊕ B) ⊕ B = Свойства операции "исключающее ИЛИ" A ⊕
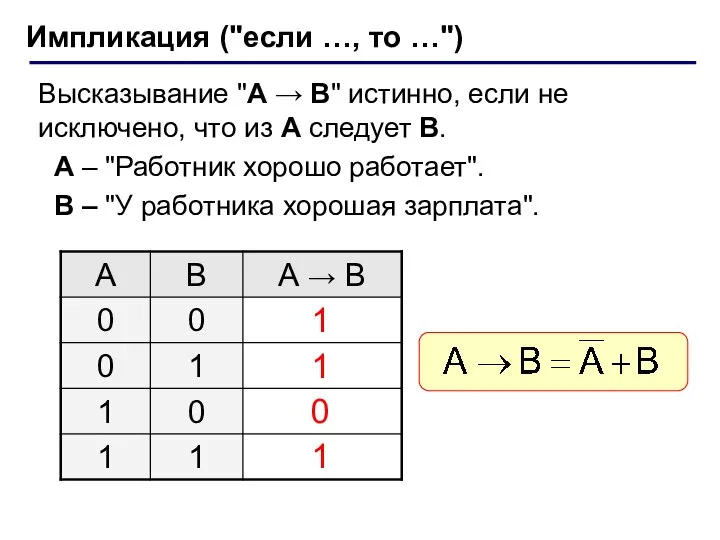
- 10. Импликация ("если …, то …") Высказывание "A → B" истинно, если не исключено, что из А
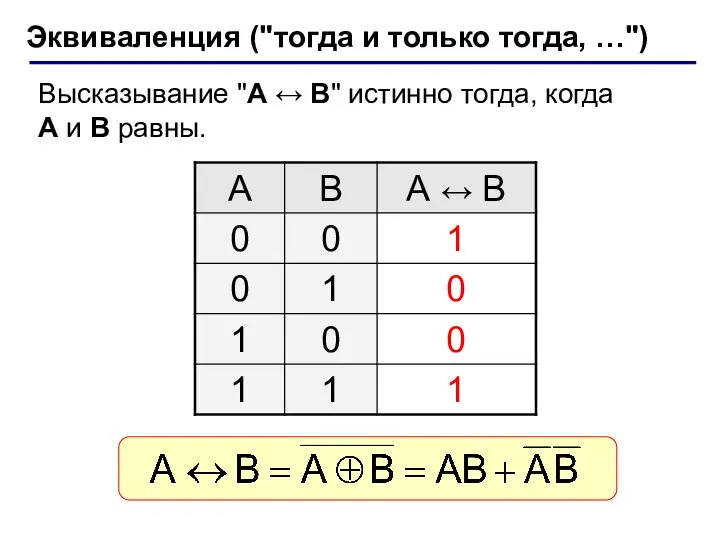
- 11. Эквиваленция ("тогда и только тогда, …") Высказывание "A ↔ B" истинно тогда, когда А и B
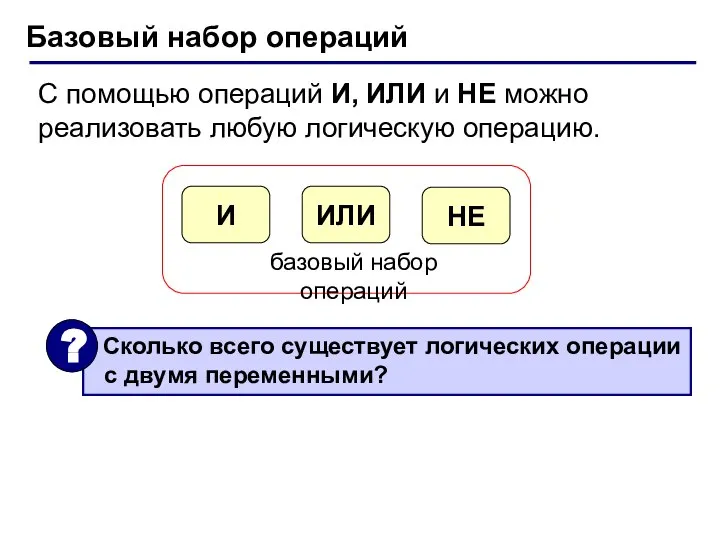
- 12. Базовый набор операций С помощью операций И, ИЛИ и НЕ можно реализовать любую логическую операцию.
- 13. Логические формулы Система имеет три датчика и может работать, если два из них исправны. A –
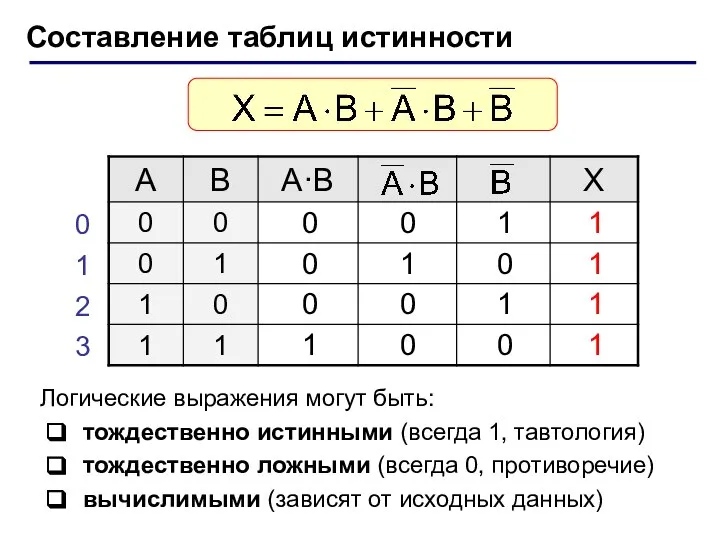
- 14. Составление таблиц истинности Логические выражения могут быть: тождественно истинными (всегда 1, тавтология) тождественно ложными (всегда 0,
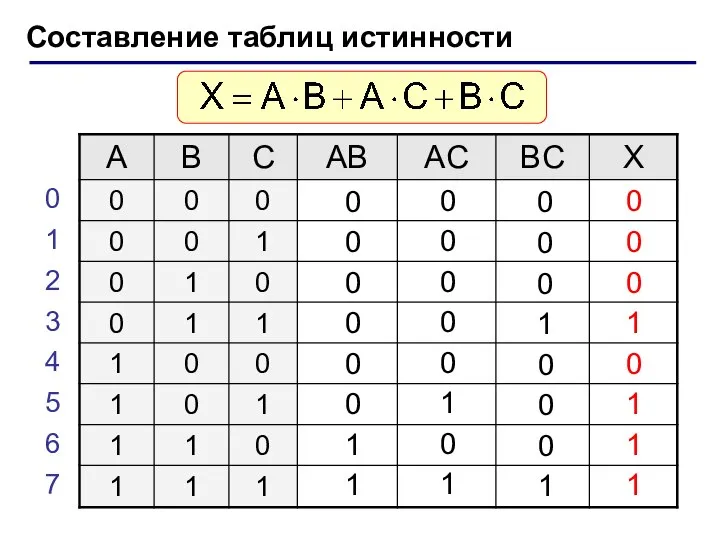
- 15. Составление таблиц истинности
- 16. Логические основы компьютеров Диаграммы
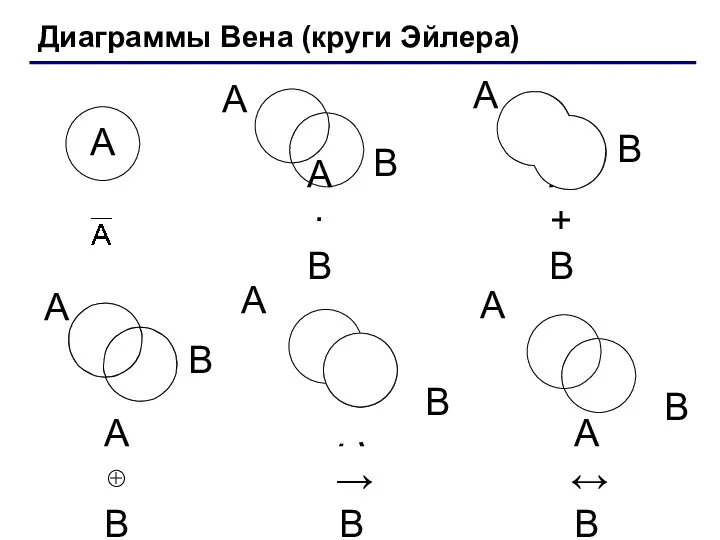
- 17. Диаграммы Вена (круги Эйлера) A·B A+B A⊕B A→B A↔B
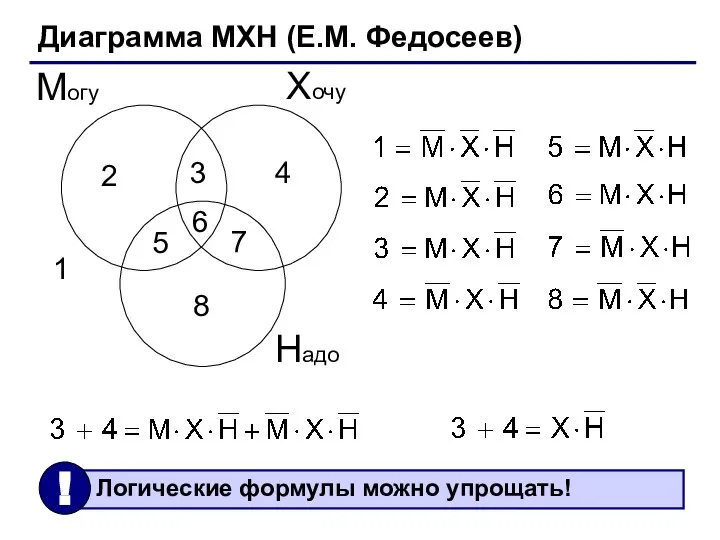
- 18. Диаграмма МХН (Е.М. Федосеев) Хочу Могу Надо 1 2 3 4 5 6 7 8
- 19. Логические основы компьютеров Преобразование логических выражений
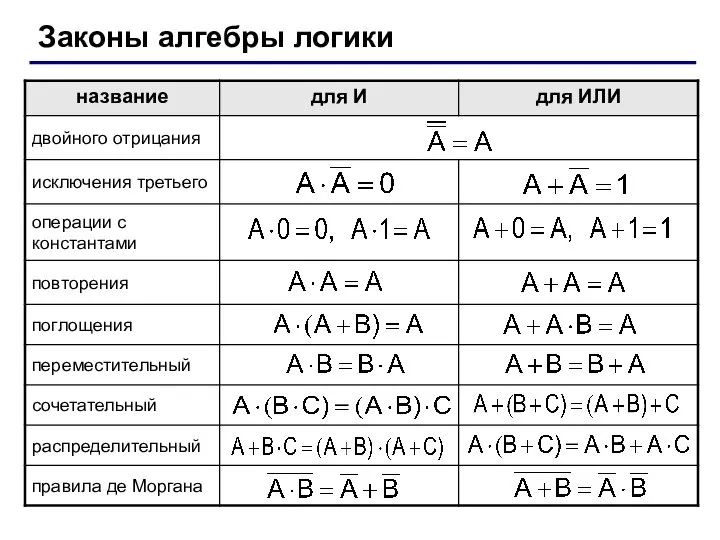
- 20. Законы алгебры логики
- 21. Упрощение логических выражений Шаг 1. Заменить операции ⊕→↔ на их выражения через И, ИЛИ и НЕ:
- 22. Упрощение логических выражений раскрыли → формула де Моргана распределительный исключения третьего повторения поглощения
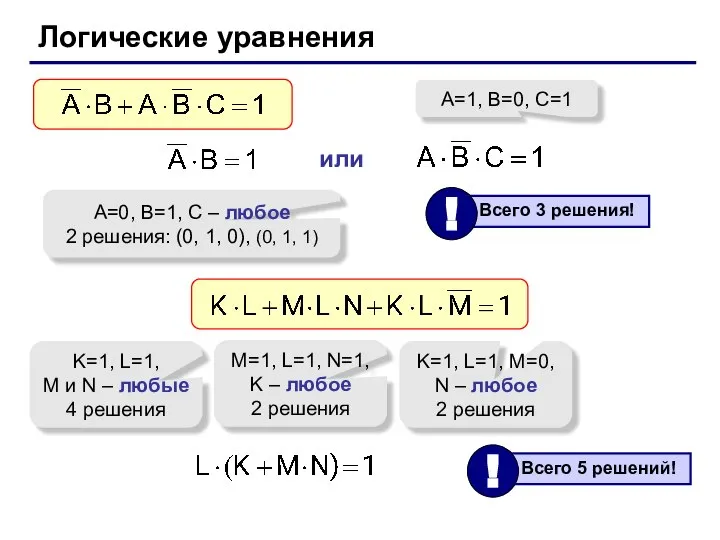
- 23. Логические уравнения A=0, B=1, C – любое 2 решения: (0, 1, 0), (0, 1, 1) или
- 24. Логические основы компьютеров Синтез логических выражений
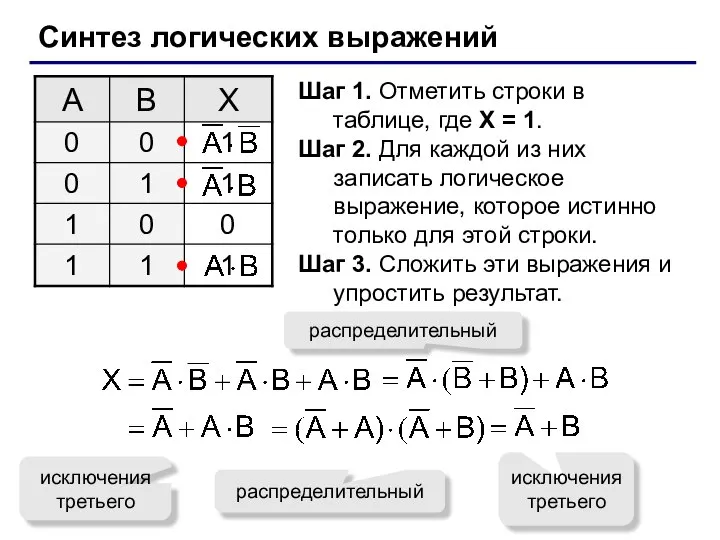
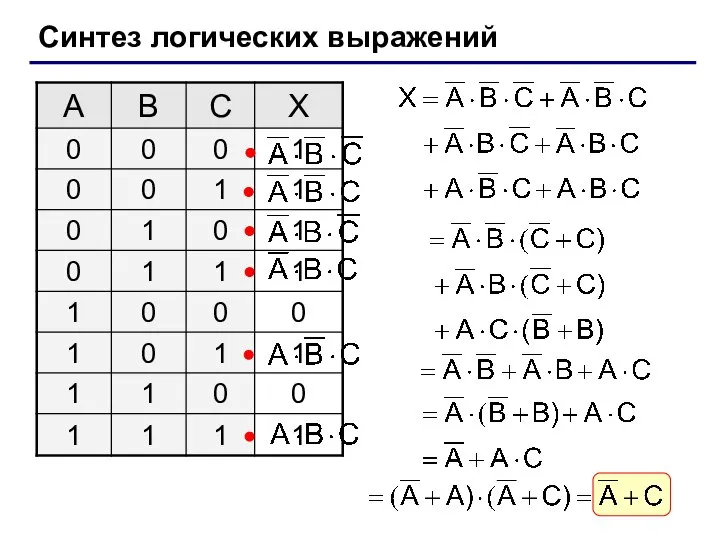
- 25. Синтез логических выражений Шаг 1. Отметить строки в таблице, где X = 1. Шаг 2. Для
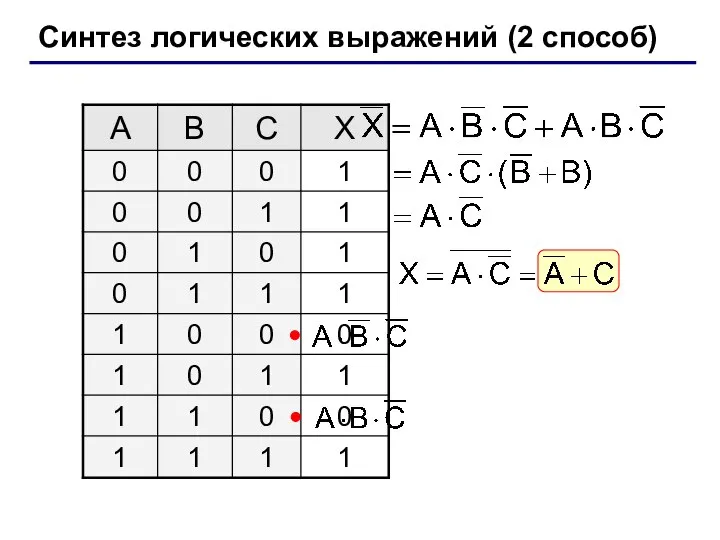
- 26. Синтез логических выражений (2 способ) Шаг 1. Отметить строки в таблице, где X = 0. Шаг
- 27. Синтез логических выражений
- 28. Синтез логических выражений (2 способ)
- 29. Логические основы компьютеров Логические элементы компьютера
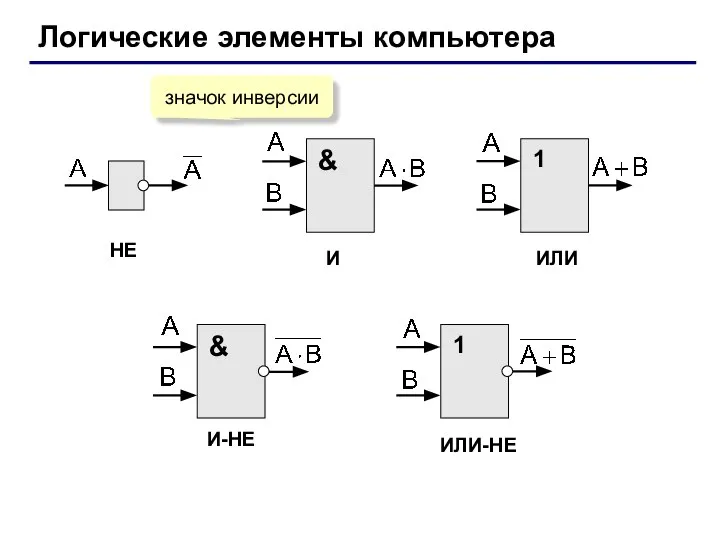
- 30. Логические элементы компьютера НЕ И ИЛИ ИЛИ-НЕ И-НЕ значок инверсии
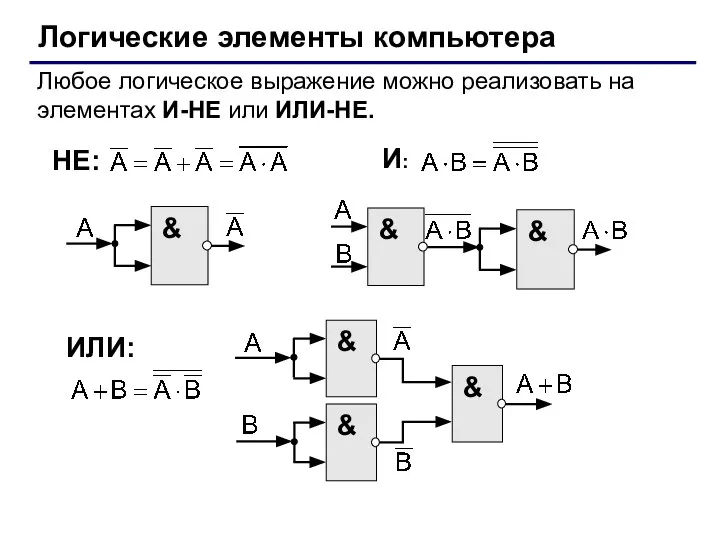
- 31. Логические элементы компьютера Любое логическое выражение можно реализовать на элементах И-НЕ или ИЛИ-НЕ. И: НЕ: ИЛИ:
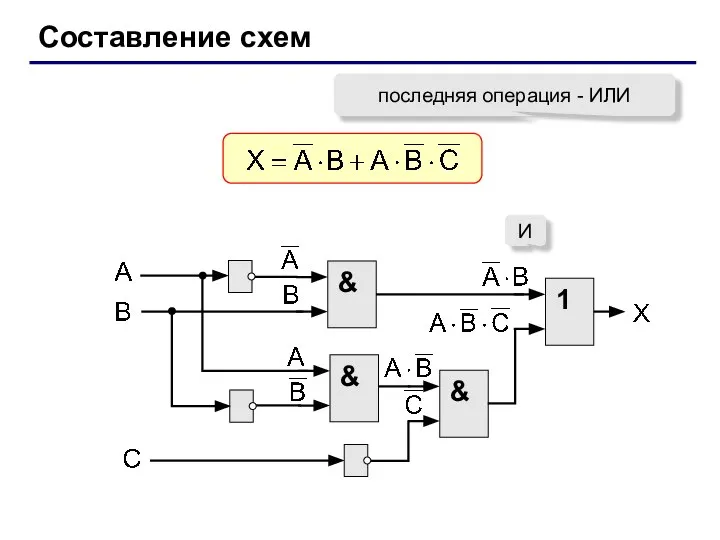
- 32. Составление схем последняя операция - ИЛИ & И
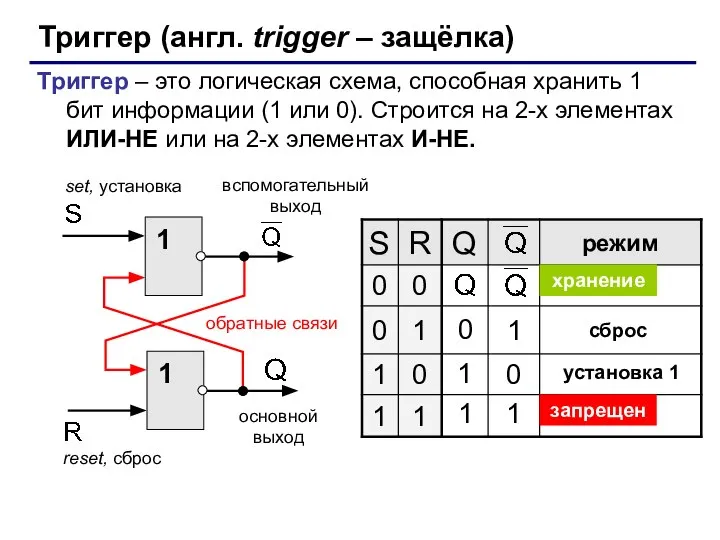
- 33. Триггер (англ. trigger – защёлка) Триггер – это логическая схема, способная хранить 1 бит информации (1
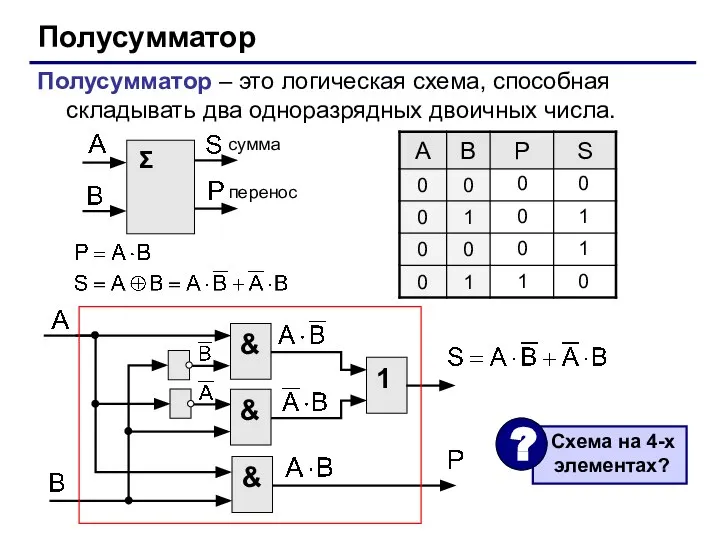
- 34. Полусумматор Полусумматор – это логическая схема, способная складывать два одноразрядных двоичных числа. 0 0 0 1
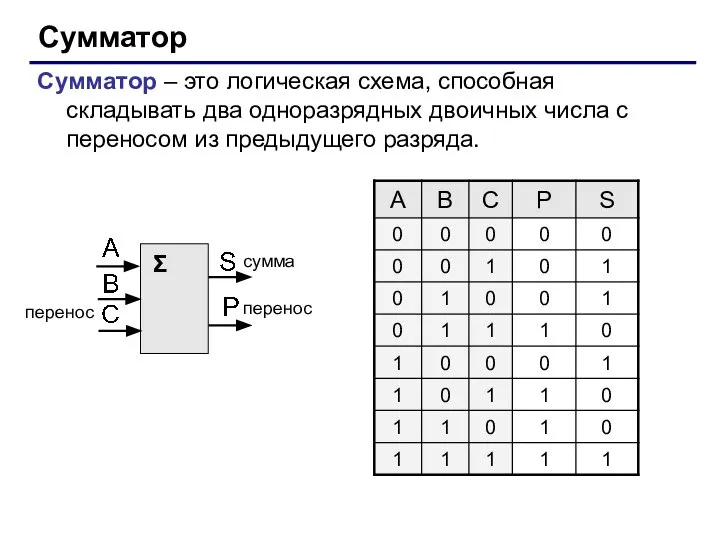
- 35. Сумматор Сумматор – это логическая схема, способная складывать два одноразрядных двоичных числа с переносом из предыдущего
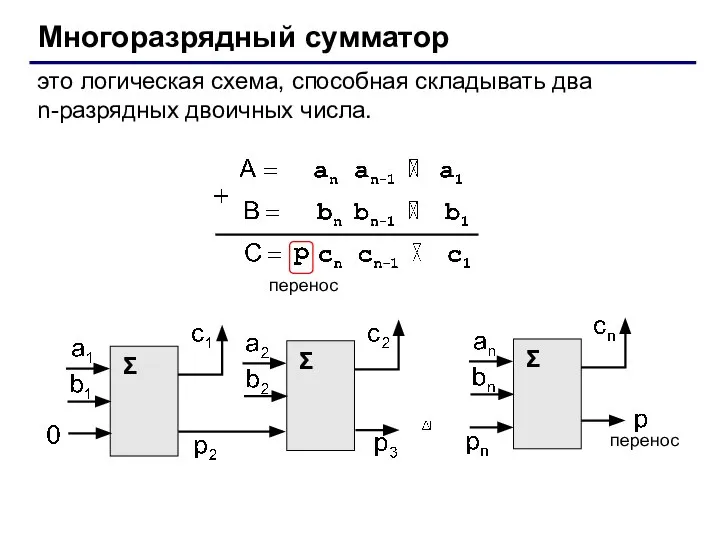
- 36. Многоразрядный сумматор это логическая схема, способная складывать два n-разрядных двоичных числа. перенос перенос
- 37. Логические основы компьютеров Логические задачи
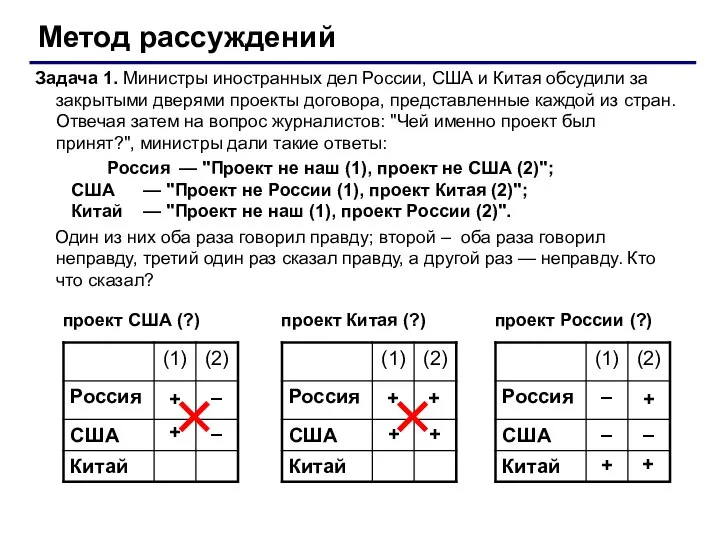
- 38. Метод рассуждений Задача 1. Министры иностранных дел России, США и Китая обсудили за закрытыми дверями проекты
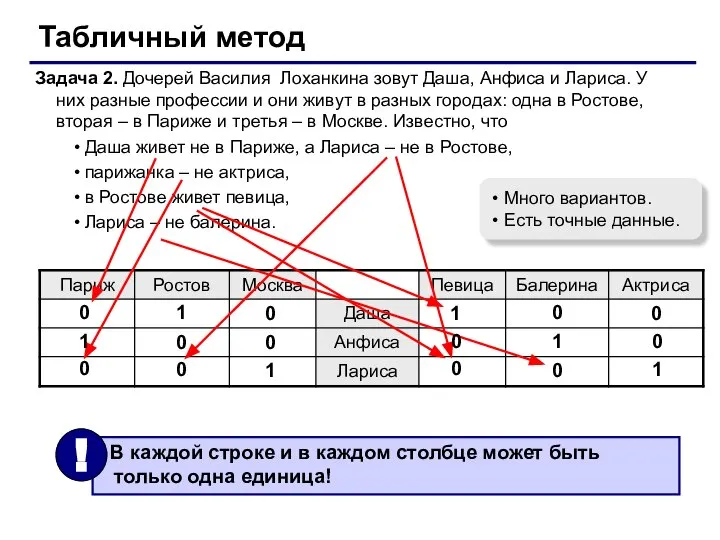
- 39. Табличный метод Задача 2. Дочерей Василия Лоханкина зовут Даша, Анфиса и Лариса. У них разные профессии
- 40. Задача Эйнштейна Условие: Есть 5 домов разного цвета, стоящие в ряд. В каждом доме живет по
- 41. Использование алгебры логики Задача 3. Следующие два высказывания истинны: 1. Неверно, что если корабль A вышел
- 43. Скачать презентацию














 Греция. Ахейцы, гомеровский период
Греция. Ахейцы, гомеровский период МСБО 18 Дохід
МСБО 18 Дохід  Тема 4. Контрактные отношения Окончание
Тема 4. Контрактные отношения Окончание  My favorite sport is football
My favorite sport is football Проблема сохранения биологического и ландшафтного разнообразия
Проблема сохранения биологического и ландшафтного разнообразия  ЛЕКЦИЯ 4 АЛЬВЕОЛЯТЫ. ТИП ДИНОФИТОВЫЕ (DINOPHYTA). ТИП ПЕРЕДНЕКОМПЛЕКСНЫЕ (APICOMPLEXA) 1 Характеристика альвеолят 2 Особенности строения
ЛЕКЦИЯ 4 АЛЬВЕОЛЯТЫ. ТИП ДИНОФИТОВЫЕ (DINOPHYTA). ТИП ПЕРЕДНЕКОМПЛЕКСНЫЕ (APICOMPLEXA) 1 Характеристика альвеолят 2 Особенности строения  PHONE STAGE
PHONE STAGE Твой бюджет. Благоустройство детской площадки. Пулковский парк в Московском районе
Твой бюджет. Благоустройство детской площадки. Пулковский парк в Московском районе Психические свойства личности: способности
Психические свойства личности: способности Трансформатор. Радіохвилі
Трансформатор. Радіохвилі История лыжного спорта
История лыжного спорта Презентация О мерах региональной политики по созданию благоприятной среды для инвестиций в инновации
Презентация О мерах региональной политики по созданию благоприятной среды для инвестиций в инновации Сестринская помощь при пиелонефритах
Сестринская помощь при пиелонефритах Поверхневі акустичні хвилі
Поверхневі акустичні хвилі Крутова Раиса Александровна Старший воспитатель ГДОУ детский сад 120 Выборгский район Санкт-Петербург
Крутова Раиса Александровна Старший воспитатель ГДОУ детский сад 120 Выборгский район Санкт-Петербург Понятие и причины текучести кадров.
Понятие и причины текучести кадров. Трудовая деятельность. Рынок труда.
Трудовая деятельность. Рынок труда. СРОКИ ПРИЕМА НА РАБОТУ СОТРУДНИКОВ, ПРИВЛЕКАЕМЫХ ДЛЯ ВЫПОЛНЕНИЯ ПРОЕКТОВ ПО ПРОГРАММЕ ФИ В 2012 ГОДУ 01 февраля 2012 г. – 31 декабря 2012 г
СРОКИ ПРИЕМА НА РАБОТУ СОТРУДНИКОВ, ПРИВЛЕКАЕМЫХ ДЛЯ ВЫПОЛНЕНИЯ ПРОЕКТОВ ПО ПРОГРАММЕ ФИ В 2012 ГОДУ 01 февраля 2012 г. – 31 декабря 2012 г Государственное бюджетное образовательное учреждение высшего профессионального образования «Оренбургская государственная мед
Государственное бюджетное образовательное учреждение высшего профессионального образования «Оренбургская государственная мед Презентация на тему "Введение предмета «Самопознание» в организациях образования Акмолинской области с 2010-2011 учебного года"
Презентация на тему "Введение предмета «Самопознание» в организациях образования Акмолинской области с 2010-2011 учебного года"  Договор на оказание туристических услуг
Договор на оказание туристических услуг Философия как социокультурный феномен
Философия как социокультурный феномен Интродукция в селекции растений
Интродукция в селекции растений  Презентация на тему "Безболевая ишемия миокарда" - скачать презентации по Медицине
Презентация на тему "Безболевая ишемия миокарда" - скачать презентации по Медицине Государственная политика в религиозной сфере
Государственная политика в религиозной сфере ТЕМА УРОКА: СУЩНОСТЬ И ФУНКЦИИ ДЕНЕГ «Даже любовь не свела с ума стольких людей, сколько
ТЕМА УРОКА: СУЩНОСТЬ И ФУНКЦИИ ДЕНЕГ «Даже любовь не свела с ума стольких людей, сколько  Гид по контенту для ТВ
Гид по контенту для ТВ Аттестационная работа. Влияние спортивной специализации на формирование типа телосложения
Аттестационная работа. Влияние спортивной специализации на формирование типа телосложения