Содержание
- 2. Он вычисляет и хранит только информацию, необходимую на данный момент, а важные данные передает в более
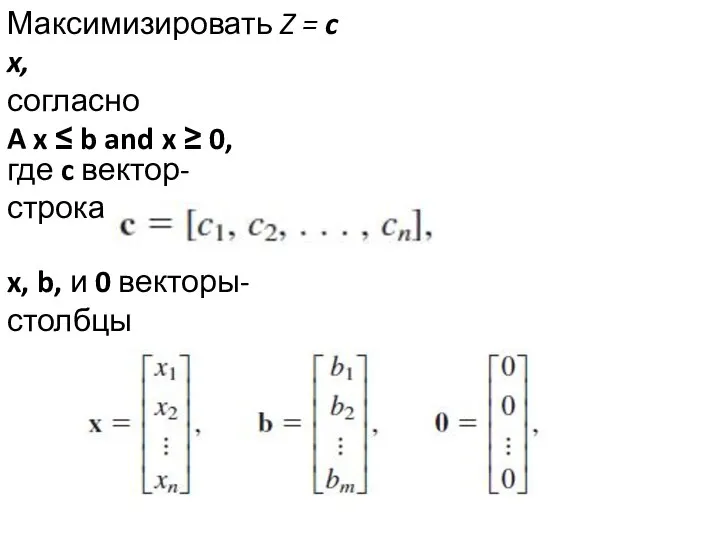
- 3. Максимизировать Z = c x, согласно A x ≤ b and x ≥ 0, где c
- 4. A - матрица Для дополненной формы, вектор-столбец фиктивных переменных: Ограничения : I = (m × m
- 5. Нахождение базового допустимого решения Общий подход симплекс-метода – получение последовательности улучшающихся ОД решений до тех пор,
- 6. Исключая эти n переменных приравниванием к нулю, получаем систему уравнений m с m переменными (основными (базисными)
- 7. И базисная матрица Полученная исключением столбцов, соответствующих коэффициентам небазисных переменных из [A, I]. (В дополнение, элементы
- 8. cB – вектор, чьи элементы - коэффициенты целевых функций (включая нули для фиктивных переменных) для соответствующих
- 9. Пример: - Итерация 0 so so
- 10. - Итерация 1 so so
- 11. - Итерация 2 so so
- 12. Матричная форма для текущего множества уравнений Матричная форма для множества уравнений, появляющаяся в симплекс-таблице для любой
- 14. Эта матрица будет иметь те же элементы, что и единичная матрица, за исключением того, что каждое
- 15. Так как мы выполняем одни и те же серии алгебраических операций с обеими сторонами исходного множества,
- 16. Example: матричная форма, полученная после итерации 2 для задачи о стекольном заводе, используя B-1 и cB:
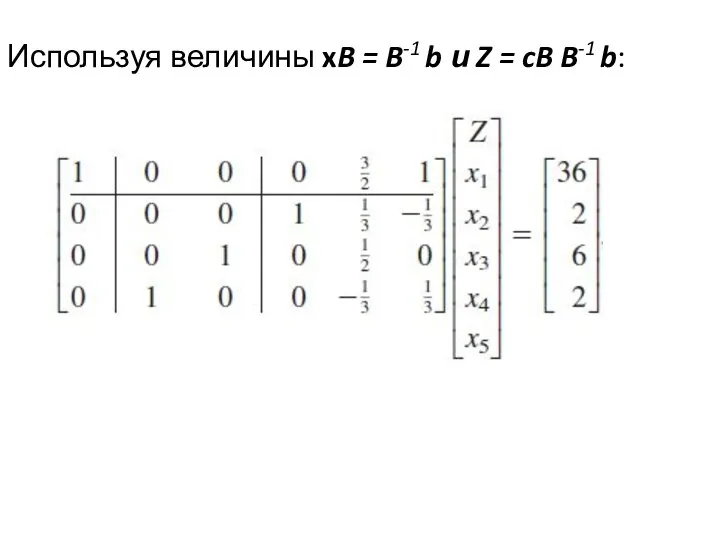
- 17. Используя величины xB = B-1 b и Z = cB B-1 b:
- 18. Только B-1 должна быть получена для вычисления всех чисел симплекс-таблицы из исходных параметров задачи (A, b,
- 20. Скачать презентацию















 Электрофизикохимические методы обработки
Электрофизикохимические методы обработки Экология и Экономика Королев Юрий Юрьевич ICS Group, President
Экология и Экономика Королев Юрий Юрьевич ICS Group, President Благоустройство участка набережной реки Охты
Благоустройство участка набережной реки Охты Предложение по реформе политической партии «Родная Партия»
Предложение по реформе политической партии «Родная Партия» Счётчики посещений. Статистика (03)
Счётчики посещений. Статистика (03) Кинотеатр Калевала
Кинотеатр Калевала Механизмы клеточной смерти Лабораторная гемоцитология
Механизмы клеточной смерти Лабораторная гемоцитология Острая ревматическая лихорадка Зав. кафедрой проф. д.мед.н. Чурилина А.В.
Острая ревматическая лихорадка Зав. кафедрой проф. д.мед.н. Чурилина А.В. ФГБОУ вПО «ЧУВАШСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ ИМ. И.Н. УЛЬЯНОВА» КАФЕДРА «СТОМАТОЛОГИИ ДЕТСКОГО ВОЗРАСТА» Введение в профилак
ФГБОУ вПО «ЧУВАШСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ ИМ. И.Н. УЛЬЯНОВА» КАФЕДРА «СТОМАТОЛОГИИ ДЕТСКОГО ВОЗРАСТА» Введение в профилак Хоку Хоку
Хоку Хоку Современная фармакотерапия эпилепсии у детей Милованова О.А.
Современная фармакотерапия эпилепсии у детей Милованова О.А. Вставка и удаление элементов массива
Вставка и удаление элементов массива Геоинформационные системы
Геоинформационные системы Презентация "Рынок факторов производства: рынок земли" - скачать презентации по Экономике
Презентация "Рынок факторов производства: рынок земли" - скачать презентации по Экономике Реабилитация в уголовном судопроизводстве Подготовила_Журавлёва Елена_Ю 093
Реабилитация в уголовном судопроизводстве Подготовила_Журавлёва Елена_Ю 093 Развития транспортной инфраструктуры Санкт-Петербурга
Развития транспортной инфраструктуры Санкт-Петербурга  Сортировка массива. Метод пузырька
Сортировка массива. Метод пузырька Валютный рынок и конвертируемость валют Экономика, профильный уровень, 11 класс, учитель Г.И. Непершина, МОУ СОШ № 15 г. Балашова Сар
Валютный рынок и конвертируемость валют Экономика, профильный уровень, 11 класс, учитель Г.И. Непершина, МОУ СОШ № 15 г. Балашова Сар 12/2011 22.08-11.09 Учиться...Учиться?...Учиться!!! СНОВА В ШКОЛУ!... в школу КРАСОТЫ. - презентация_
12/2011 22.08-11.09 Учиться...Учиться?...Учиться!!! СНОВА В ШКОЛУ!... в школу КРАСОТЫ. - презентация_ Заклепочные соединения
Заклепочные соединения Тепловой насос. Принцип его действия
Тепловой насос. Принцип его действия Презентация Государственная регистрация объектов недвижимости
Презентация Государственная регистрация объектов недвижимости Гражданское процессуальное право Общая часть
Гражданское процессуальное право Общая часть Умножение в Простоквашино - презентация для начальной школы
Умножение в Простоквашино - презентация для начальной школы Производство сыра
Производство сыра Сөйлемнің құрылымы
Сөйлемнің құрылымы Наблюдение и уход за пациентами пожилого и старческого возраста
Наблюдение и уход за пациентами пожилого и старческого возраста Сервитутное право
Сервитутное право