Содержание
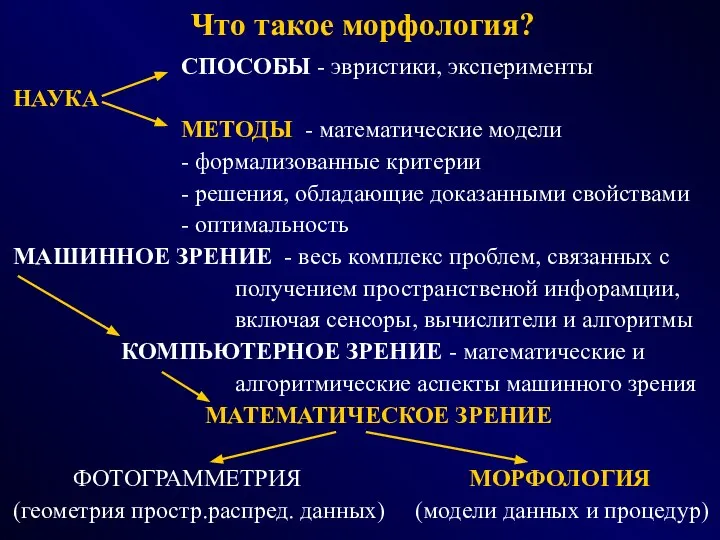
- 2. Что такое морфология? СПОСОБЫ - эвристики, эксперименты НАУКА МЕТОДЫ - математические модели - формализованные критерии -
- 3. Что такое морфология? Термин: Морфология – (1) «наука о форме»; (2) методы анализа изображений, основанные на
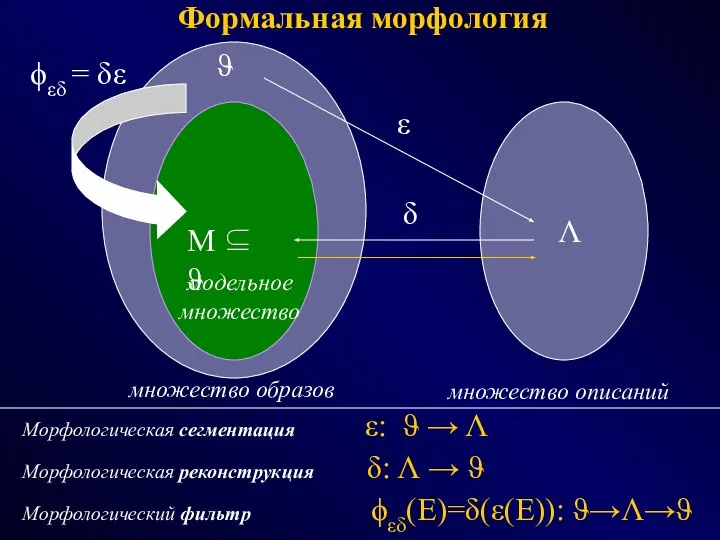
- 4. Формальная морфология ϑ Λ M ⊆ ϑ ε δ ϕεδ = δε множество образов множество описаний
- 5. Сегментация + Реконструкция множество образов множество описаний Искусственный изоморфизм Естественный гомоморфизм 568=5×102+6×101+8×10 40=1×25+1×23 28=22 × 71
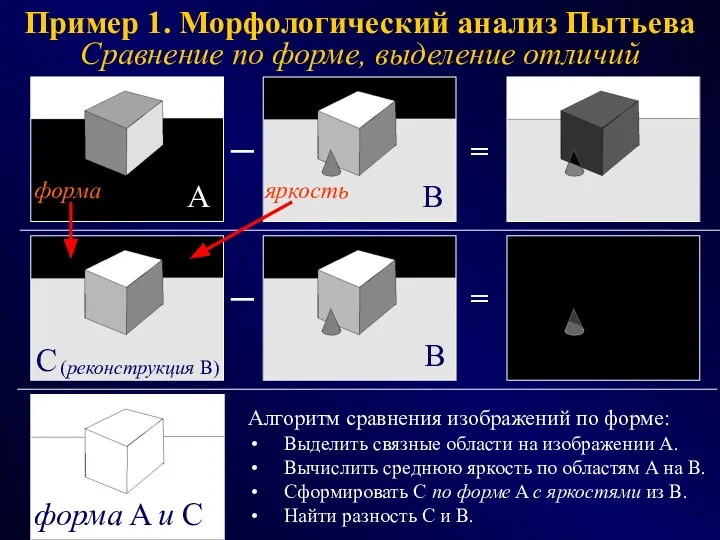
- 6. Пример 1. Морфологический анализ Пытьева Сравнение по форме, выделение отличий ─ = ─ = Алгоритм сравнения
- 7. Морфологический анализ Пытьева A1 A2 A3 A4 Индикаторная функция множества Ai Значение яркости(интенсивности) пикселя с координатами
- 8. Морфологический анализ Пытьева Проекция изображения на форму Изображение , определенное на поле Х Форма изображения V(f)
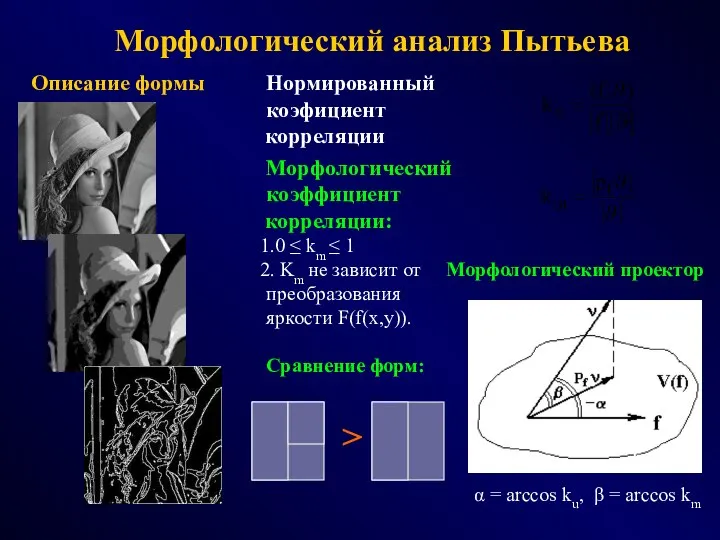
- 9. Морфологический анализ Пытьева α = arccos ku, β = arccos km Нормированный коэфициент корреляции Морфологический коэффициент
- 10. Морфологический анализ Пытьева
- 11. Пример 2. Математическая морфология Серра Обработка с учетом формы, выделение деталей MIN эрозия MAX дилатация MIN
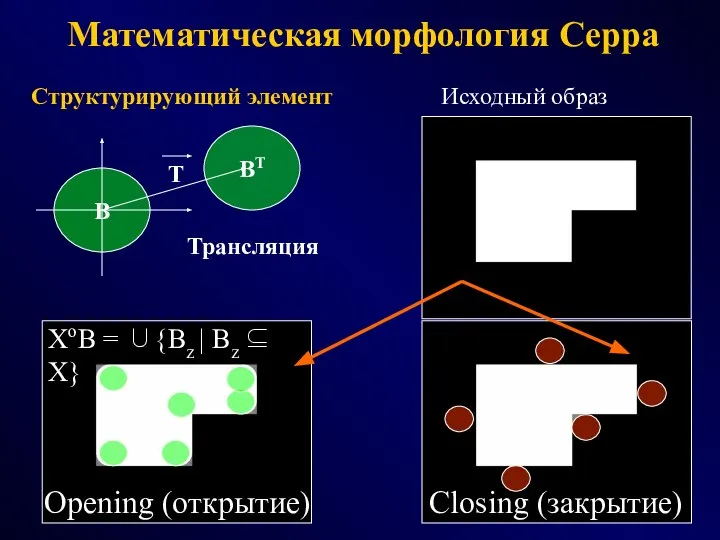
- 12. Математическая морфология Серра B BT T Структурирующий элемент Исходный образ Трансляция Opening (открытие) Closing (закрытие) XoB
- 13. Математическая морфология Серра Трансляция A по z: Az = {y| a∈A, y=a=z}. Сложение Минковского (дилатация): A⊕B
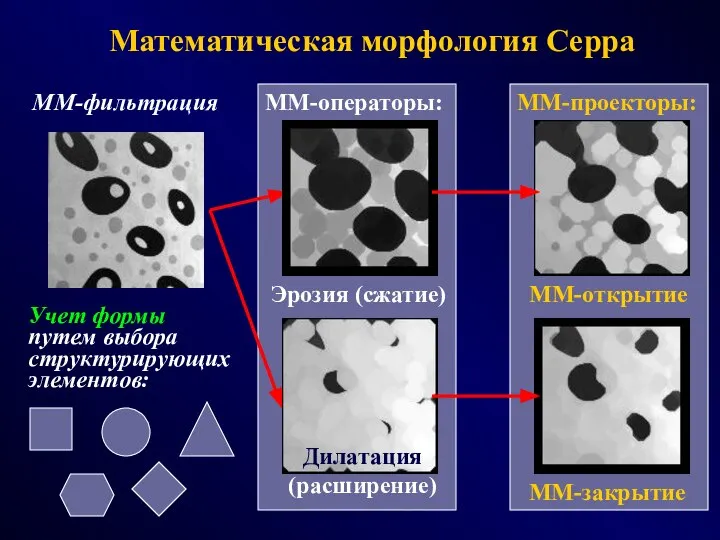
- 14. Математическая морфология Серра ММ-операторы: ММ-проекторы: Эрозия (сжатие) Дилатация (расширение) ММ-открытие ММ-закрытие ММ-фильтрация Учет формы путем выбора
- 15. Математическая морфология Серра
- 16. Пример 3. Бинарная морфология на базе скелетов A Фигурой называется связная замкнутая область плоскости, ограниченная конечным
- 17. Бинарная морфология на базе скелетов
- 18. ПРОЕКТИВНОСТЬ
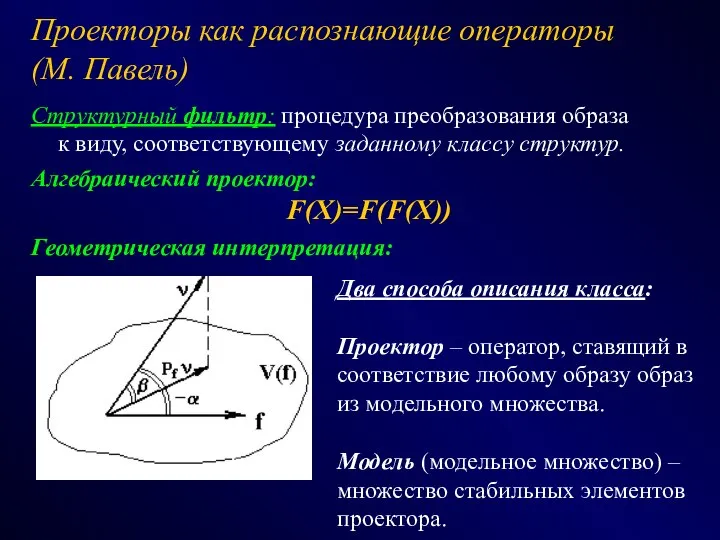
- 19. Проекторы как распознающие операторы (М. Павель) Структурный фильтр: процедура преобразования образа к виду, соответствующему заданному классу
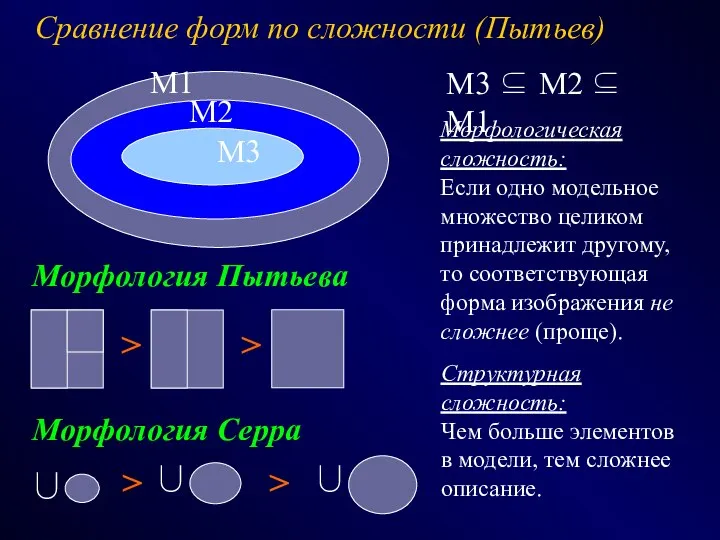
- 20. Сравнение форм по сложности (Пытьев) M1 M2 M3 M3 ⊆ M2 ⊆ M1 Морфологическая сложность: Если
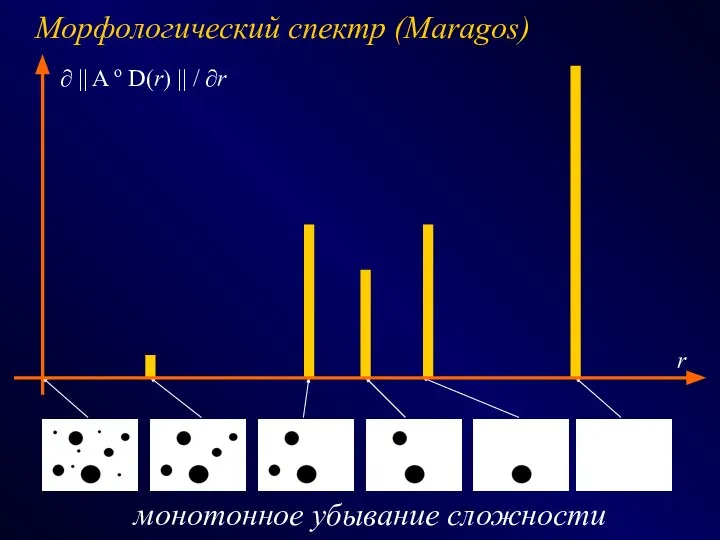
- 21. Морфологический спектр (Maragos) r ∂ || A o D(r) || / ∂r монотонное убывание сложности
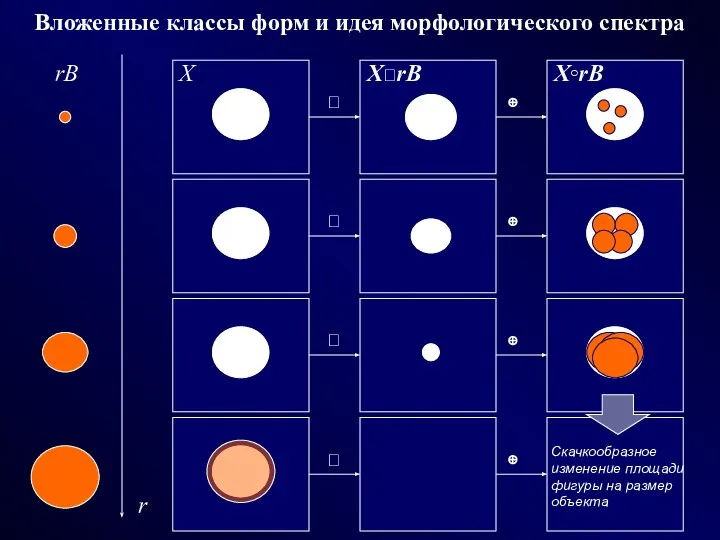
- 22. Вложенные классы форм и идея морфологического спектра ⊕ ⊕ ⊕ ⊕ r
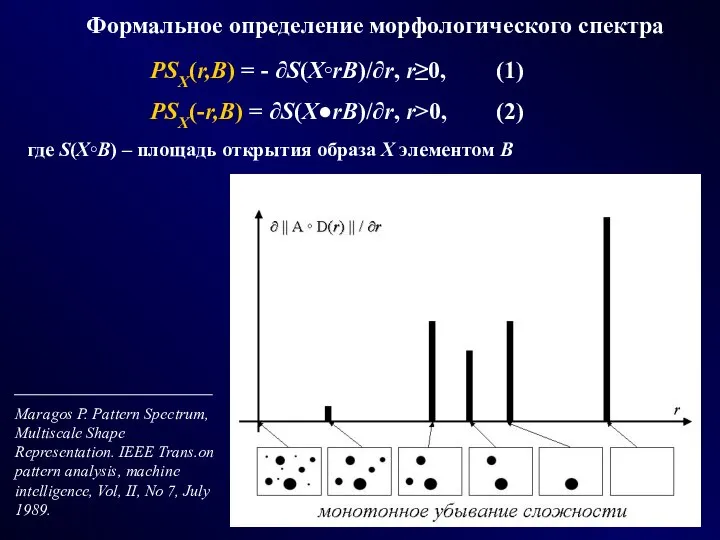
- 23. PSX(r,B) = - ∂S(X◦rB)/∂r, r≥0, (1) PSX(-r,B) = ∂S(X●rB)/∂r, r>0, (2) где S(X◦B) – площадь открытия
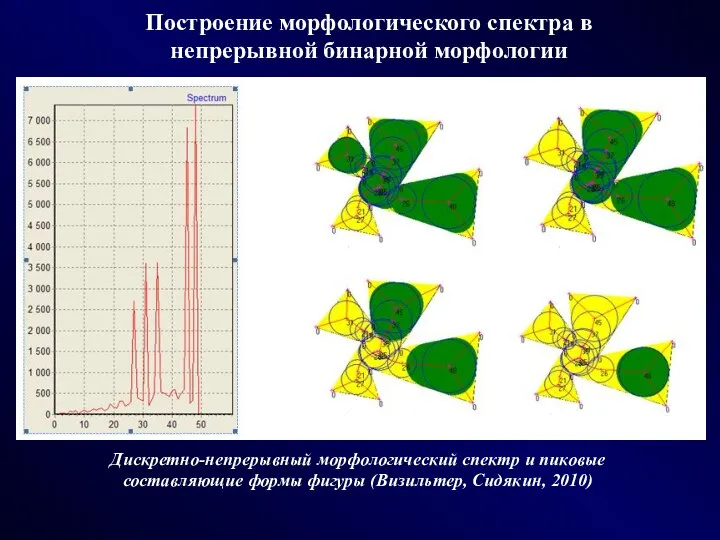
- 24. Построение морфологического спектра в непрерывной бинарной морфологии Дискретно-непрерывный морфологический спектр и пиковые составляющие формы фигуры (Визильтер,
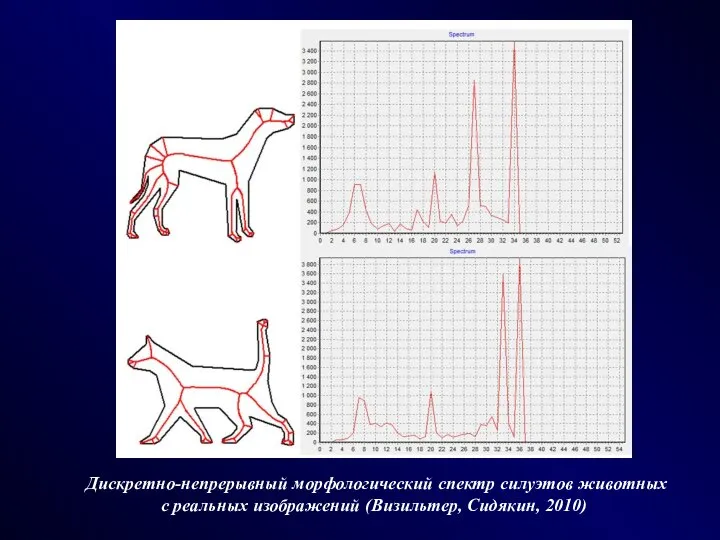
- 25. Дискретно-непрерывный морфологический спектр силуэтов животных с реальных изображений (Визильтер, Сидякин, 2010)
- 26. МОДУЛЬНОСТЬ (комбинирование процедур)
- 27. Альтернативные модульные морфологии Идея: Построение различных модульных морфологических операторов путем комбинирования разных операторов сегментации с разными
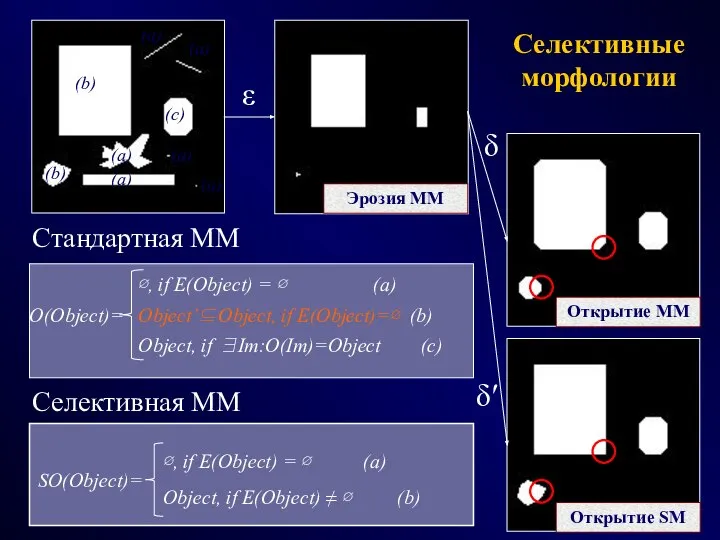
- 28. Селективные морфологии (a) (b) (c) (a) (b) (a) (a) Открытие MM (a) (a) O(Object)= ∅, if
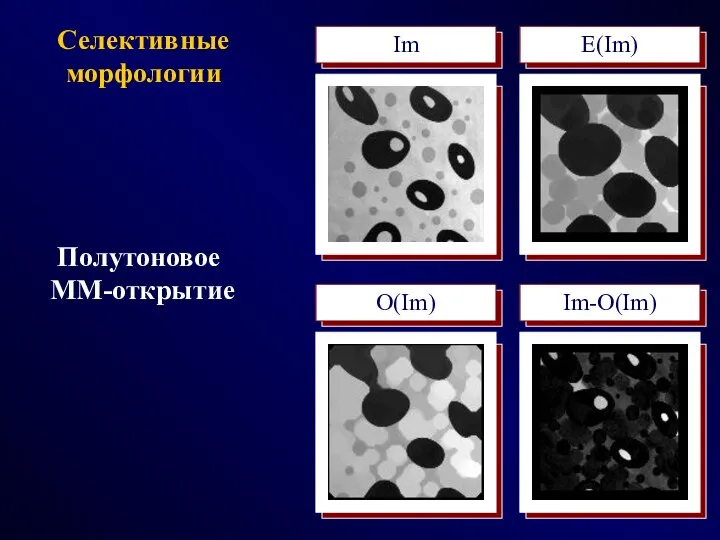
- 29. Селективные морфологии Im E(Im) O(Im) Im-O(Im) Полутоновое MM-открытие
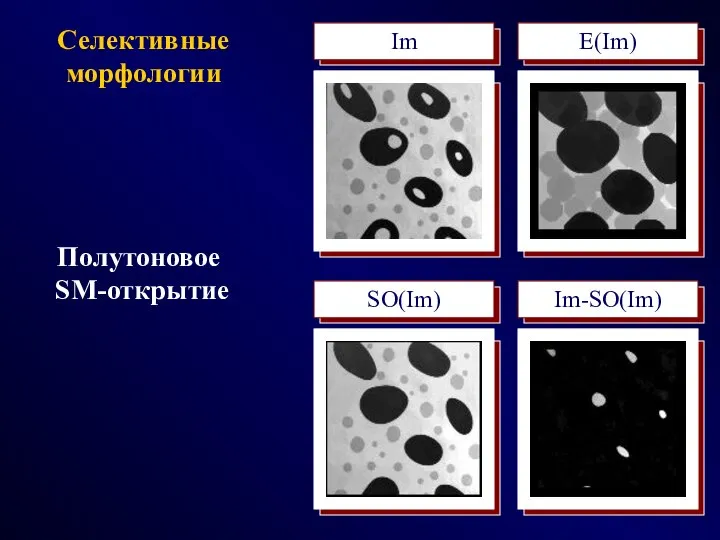
- 30. Селективные морфологии Полутоновое SM-открытие Im E(Im) SO(Im) Im-SO(Im)
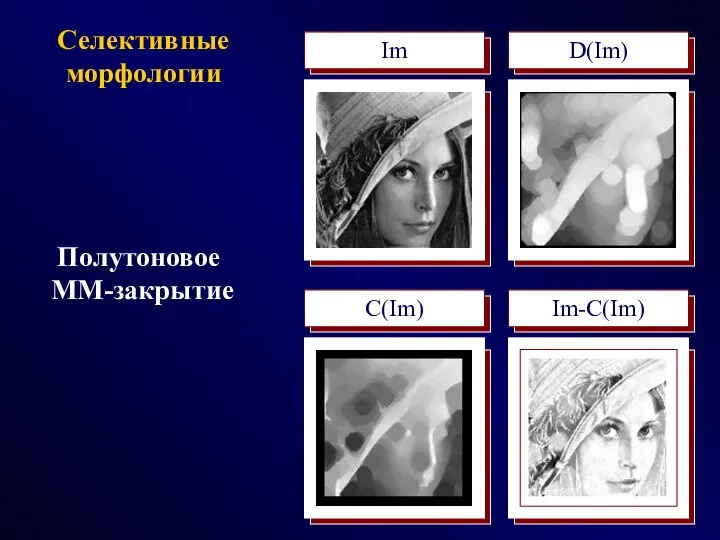
- 31. Селективные морфологии Im D(Im) C(Im) Im-C(Im) Полутоновое MM-закрытие
- 32. Селективные морфологии Im D(Im) SC(Im) Im-SC(Im) Полутоновое SM-закрытие
- 33. Селективные морфологии Полутоновое MM-открытие Im E(Im) O(Im) Im-O(Im)
- 34. Селективные морфологии Полутоновое SM-открытие Im E(Im) SO(Im) Im-SO(Im)
- 35. Селективные морфологии Полутоновое MM-закрытие Im D(Im) C(Im) Im-C(Im)
- 36. Селективные морфологии Полутоновое SM-закрытие Im D(Im) SC(Im) Im-SC(Im)
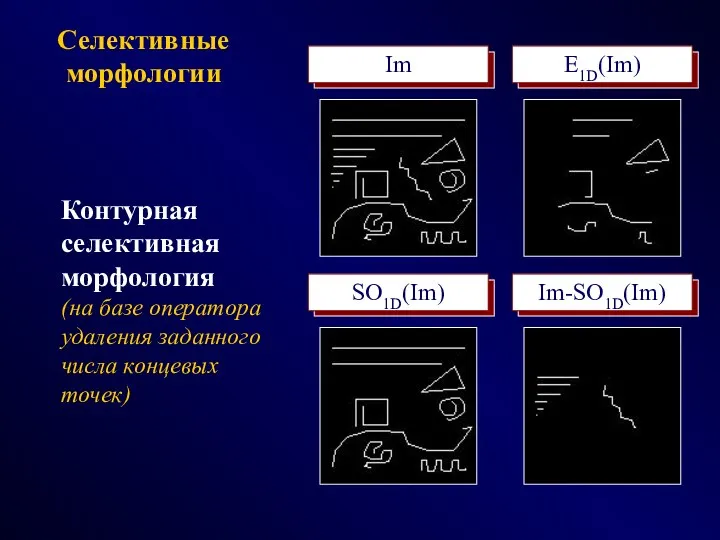
- 37. Селективные морфологии Im E1D(Im) SO1D(Im) Im-SO1D(Im) Контурная селективная морфология (на базе оператора удаления заданного числа концевых
- 38. МОРФОЛОГИЧЕСКИЙ АНАЛИЗ НА БАЗЕ КРИТЕРИЕВ (сегментация с регуляризацией)
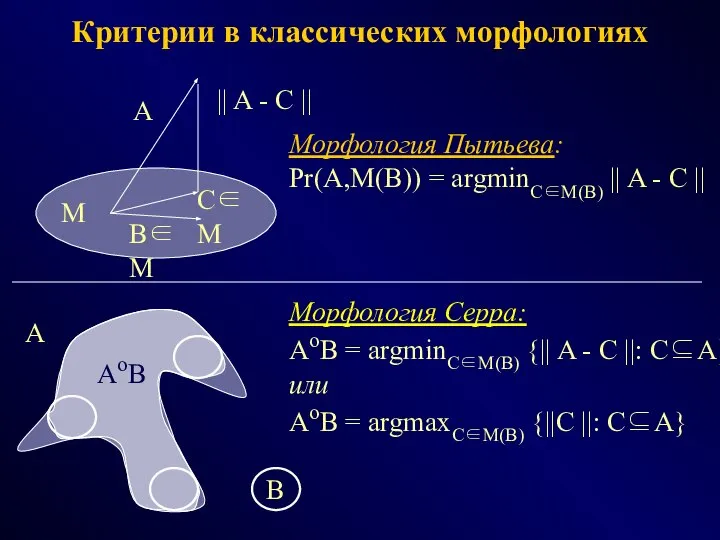
- 39. Критерии в классических морфологиях Морфология Пытьева: Pr(A,M(B)) = argminC∈M(B) || A - C || Морфология Серра:
- 40. Критериальная морфология: Модель: M(λ): Λ→[0,1] ⇔ M(L):ϑ→[0,1] Критерий соответствия: K(E,λ): ϑ×Λ→[0,1] ⇔ K(E,L): ϑ×ϑ→[0,1] Критериальный морфологический
- 41. Морфологическое решение задач анализа данных: 1. Фильтрация ϕФ(E)=δ(λ): 2. Сегментация εФ(E)=λ: Ф(E,λ)=K(E,δ(λ))×M(λ)→max(λ∈Λ) 3. Распознавание cФ(E)=H: Ф(E,λ,H)=K(E,δ(λ))×M(λ,H)×M(H)→max(λ∈Λ,H∈Θ)
- 42. Нечеткие модели: [0,1] Максимум достоверности: Ф(A,L)=K(A,L)×M(L)→max(L∈Ω) Вероятностные модели: [0,1] Максимум апостериорной вероятности ψ(A)=L: P(A,L)=P(A/L)×P(L)→max(L∈Ω). Четкие или
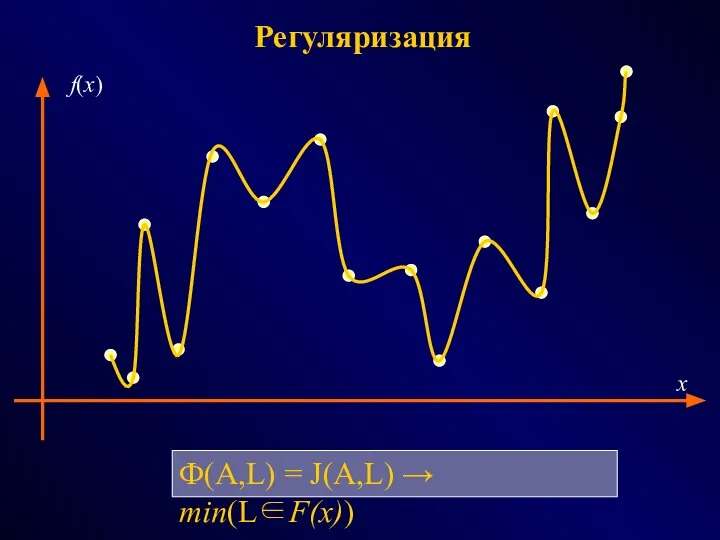
- 43. Регуляризация Ф(A,L) = J(A,L) → min(L∈F(x)) x f(x)
- 44. Регуляризация Ф(A,L) = J(A,L) → min(L∈F(x)) x f(x)
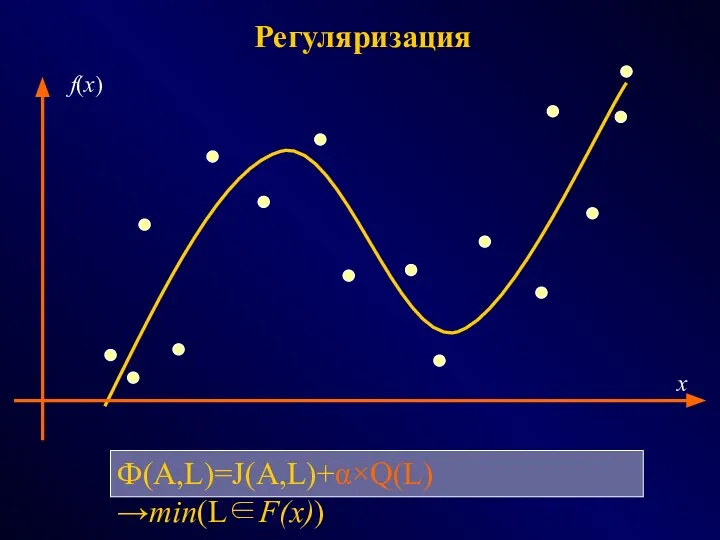
- 45. Регуляризация Ф(A,L)=J(A,L)+α×Q(L)→min(L∈F(x)) x f(x)
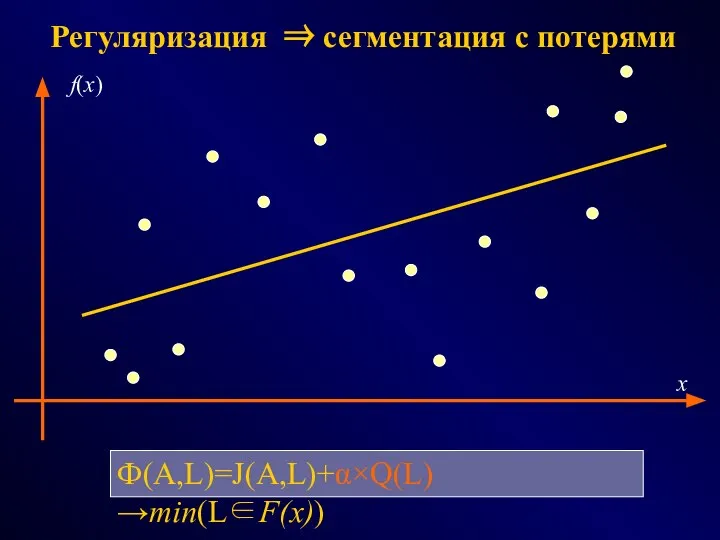
- 46. Регуляризация ⇒ сегментация с потерями Ф(A,L)=J(A,L)+α×Q(L)→min(L∈F(x)) x f(x)
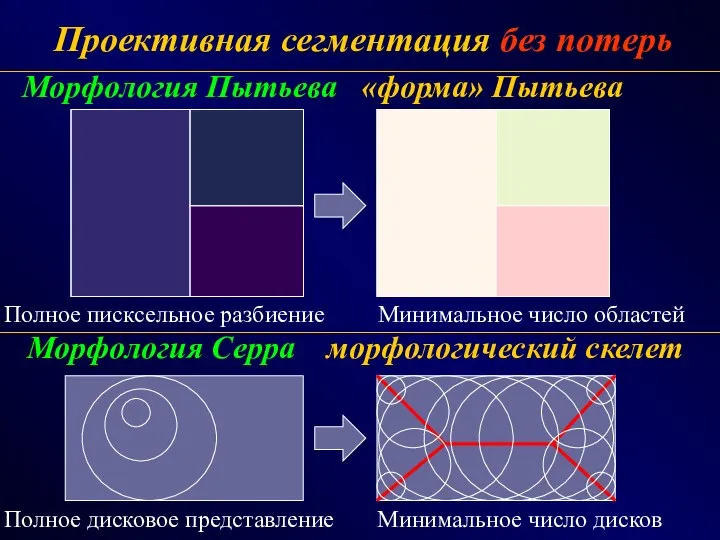
- 47. Проективная сегментация без потерь Морфология Пытьева «форма» Пытьева Морфология Серра морфологический скелет Минимальное число областей Минимальное
- 48. Критериальные проективные морфологии Пусть имеется множество образов Ω, на котором определена операция сложения (‘+’), задающая на
- 49. Стандартный критерий штрафа Ф(A,B)= J(A,B) + χ(A,B) + α×Q(B) где J(A,B) – критерий соответствия проекции и
- 50. Достаточные условия построения проективных операторов Ф(A,B)= J(A,B) + χ(A,B) + α×Q(B) Критериальные проективные морфологии
- 52. Скачать презентацию



















![Критериальная морфология: Модель: M(λ): Λ→[0,1] ⇔ M(L):ϑ→[0,1] Критерий соответствия: K(E,λ): ϑ×Λ→[0,1]](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/1295772/slide-39.jpg)

![Нечеткие модели: [0,1] Максимум достоверности: Ф(A,L)=K(A,L)×M(L)→max(L∈Ω) Вероятностные модели: [0,1] Максимум апостериорной](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/1295772/slide-41.jpg)




 Братья Гримм
Братья Гримм Рождество. История возникновения рождественской открытки
Рождество. История возникновения рождественской открытки Экономические основы деятельности фирмы
Экономические основы деятельности фирмы  Современное украинское кино Презентацию подготовил студент 1 курса стоматологического факультета Загарук Марк
Современное украинское кино Презентацию подготовил студент 1 курса стоматологического факультета Загарук Марк  Энергетические спектры сигналов. Принципы корреляционного анализа
Энергетические спектры сигналов. Принципы корреляционного анализа Тестовая оценка знаний учащихся начальных классов Выполнила Вайс В.К., руководитель педстудии «Разновозрастный класс»
Тестовая оценка знаний учащихся начальных классов Выполнила Вайс В.К., руководитель педстудии «Разновозрастный класс» Спортивные парки Украины. Концепция
Спортивные парки Украины. Концепция Азербайджанские народные игры
Азербайджанские народные игры Пересечение поверхностей вращения
Пересечение поверхностей вращения Презентация на тему "Методы обследования больных с эндокринной патологией" - скачать презентации по Медицине
Презентация на тему "Методы обследования больных с эндокринной патологией" - скачать презентации по Медицине Мастерица-рукодельница
Мастерица-рукодельница Абай Кунанбаев
Абай Кунанбаев Организация циклов. Цикл с параметром (со счетчиком)
Организация циклов. Цикл с параметром (со счетчиком) Требования, предъявляемые к управленческим решениям. Лекция 2
Требования, предъявляемые к управленческим решениям. Лекция 2 Қазақ халқының өлім-жітім жөнелту салты
Қазақ халқының өлім-жітім жөнелту салты Как достичь успеха в профессии
Как достичь успеха в профессии Satanizm. Bądź czujn
Satanizm. Bądź czujn Очаги детского сифилиса
Очаги детского сифилиса Рекомендации родителям по укреплению здоровья детей
Рекомендации родителям по укреплению здоровья детей Русская культура первой половины XIX века. (10 класс)
Русская культура первой половины XIX века. (10 класс) Футбольный матч Украина - Македония
Футбольный матч Украина - Македония Агитационное искусство периода Первой мировой войны Материалы к уроку 11 класс
Агитационное искусство периода Первой мировой войны Материалы к уроку 11 класс Современные стандарты лечения больных ранним артритом
Современные стандарты лечения больных ранним артритом « Поговорим о ВИЧ и СПИД » Акмолинский областной центр по профилактике и борьбе со СПИД
« Поговорим о ВИЧ и СПИД » Акмолинский областной центр по профилактике и борьбе со СПИД Государство. Теории происхождения государства. Государственно-религиозные отношения
Государство. Теории происхождения государства. Государственно-религиозные отношения Исследование рынка труда в области компьютерной лингвистики Руководитель проекта – Татьяна Ландо Участники проекта Алеш
Исследование рынка труда в области компьютерной лингвистики Руководитель проекта – Татьяна Ландо Участники проекта Алеш СОВРЕМЕННЫЙ РУССКИЙ ЛИТЕРАТУРНЫЙ ЯЗЫК
СОВРЕМЕННЫЙ РУССКИЙ ЛИТЕРАТУРНЫЙ ЯЗЫК  Понятие о памяти и ее основных процессах
Понятие о памяти и ее основных процессах