Содержание
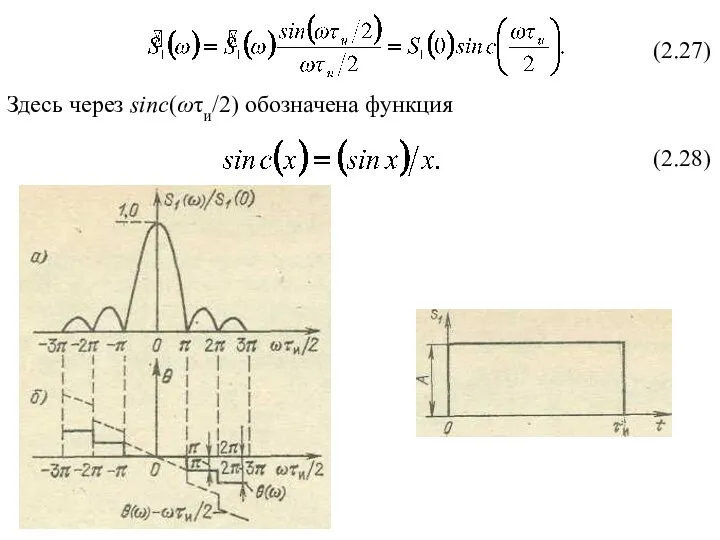
- 2. Здесь через sinc(ωτи/2) обозначена функция (2.27) (2.28)
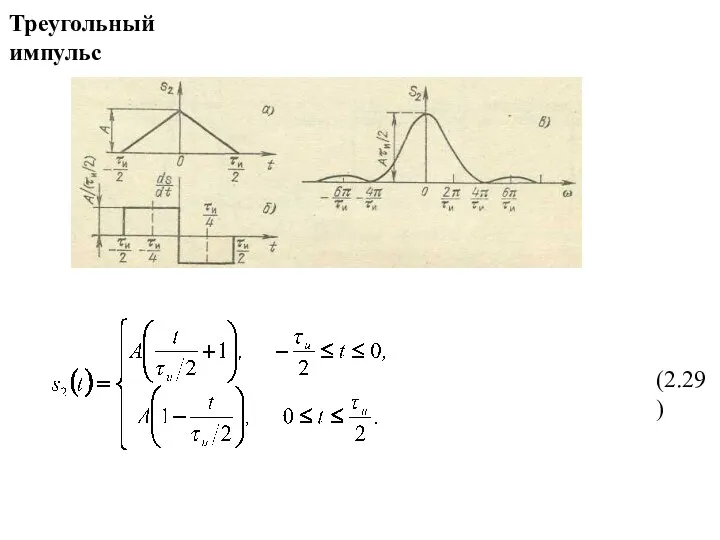
- 3. Треугольный импульс (2.29)
- 4. Спектральная плотность положительного прямоугольного импульса длительностью по аналогии с формулой (2.26) и с учетом сдвига середины
- 5. Колоколообразный (гауссовский) импульс (2.32) (2.33) Дополним показатель степени до квадрата суммы где d определяется из условия
- 6. Переходя к новой переменной , получаем Учитывая, что входящий в это выражение интеграл равен , окончательно
- 7. соответствует гауссовский импульс с длительностью и амплитудой Гауссовский импульс и его спектр выражаются одинаковыми функциями и
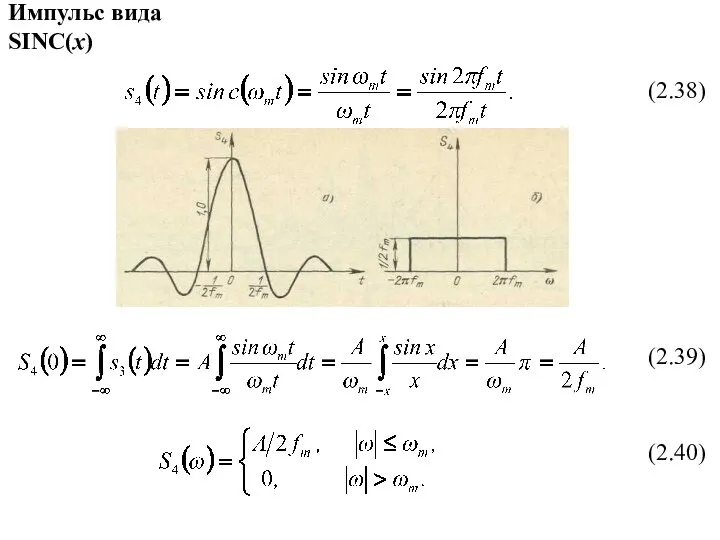
- 8. Импульс вида SINC(x) (2.38) (2.39) (2.40)
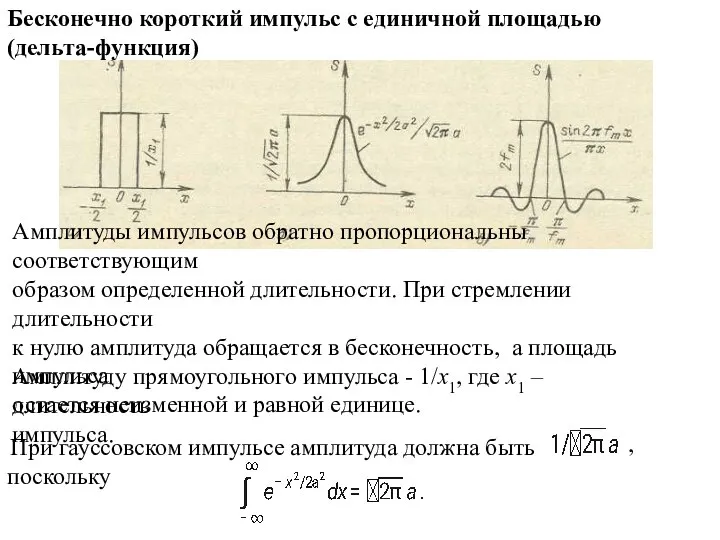
- 9. Бесконечно короткий импульс с единичной площадью (дельта-функция) Амплитуды импульсов обратно пропорциональны соответствующим образом определенной длительности. При
- 10. при одновременном условии (2.43) (2.44) Для импульса sin(2πfmx)/πx , площадь которого равна единице, амплитуда равна 2fm
- 11. Применительно к исходным функциям, дельта-функция должна быть определена выражениями При сдвиге импульса по оси х на
- 12. (2.49) В математике соотношение (2.49) называется фильтрующим (стробирующим) свойством дельта-функции. Спектральная плотность дельта-функции вещественна и равна
- 13. Спектральная плотность дельта-функции может быть получена и с помощью преобразования Фурье: Используя свойство (2.49), находим :
- 15. Скачать презентацию








 Поговорим об ушедшем лете
Поговорим об ушедшем лете  Культура Руси XVII века
Культура Руси XVII века Проект «Региональный студенческий Центр боевых искусств в Республике Марий Эл»
Проект «Региональный студенческий Центр боевых искусств в Республике Марий Эл»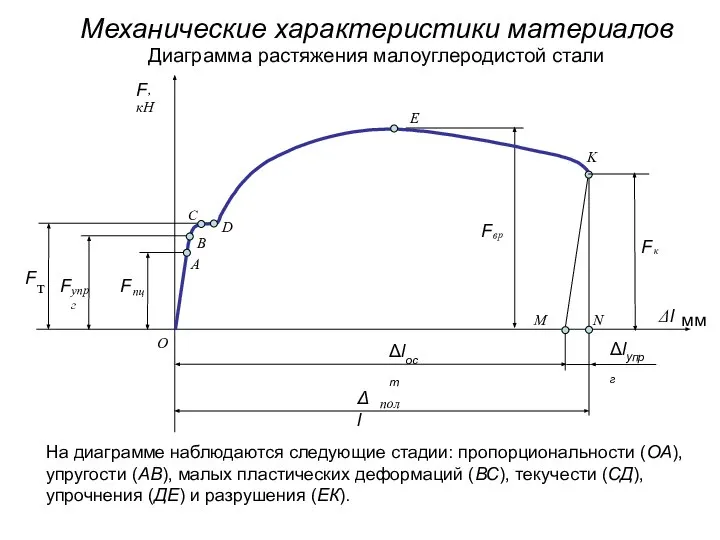 Механические характеристики материалов. Диаграмма растяжения малоуглеродистой стали
Механические характеристики материалов. Диаграмма растяжения малоуглеродистой стали Шахматные игры с ладьей. Часть 2
Шахматные игры с ладьей. Часть 2 Моделирование.pptx
Моделирование.pptx Патофизиология и ее место среди медико-биологических и клинических наук
Патофизиология и ее место среди медико-биологических и клинических наук Мы против СПИДа Подготовила: студентка 1го курса группы 444-к Моргун Марина
Мы против СПИДа Подготовила: студентка 1го курса группы 444-к Моргун Марина Программирование линейных алгоритмов
Программирование линейных алгоритмов Цыпленок - презентация для начальной школы
Цыпленок - презентация для начальной школы Презентация "Школа искусств" - скачать презентации по МХК
Презентация "Школа искусств" - скачать презентации по МХК Правовая охрана программ и данных
Правовая охрана программ и данных  УРОВНИ ОРГАНИЗАЦИИ ЖИЗНИ
УРОВНИ ОРГАНИЗАЦИИ ЖИЗНИ Усыновление. От знакомства до решения суда. Работа с родителями. Дом ребёнка № 20 г. Москва Воспитатель Антонова И.А.
Усыновление. От знакомства до решения суда. Работа с родителями. Дом ребёнка № 20 г. Москва Воспитатель Антонова И.А.  Здоровьесберегающие технологии на уроках изобразительного искусства
Здоровьесберегающие технологии на уроках изобразительного искусства Органы, осуществляющие предварительное следствие Выполнила Тарасенко Александра, студент группы Ю101
Органы, осуществляющие предварительное следствие Выполнила Тарасенко Александра, студент группы Ю101 Виды соединений
Виды соединений Public area mark up
Public area mark up Презентация на тему "Воспитательная система МБОУ «Каратузская СОШ»" - скачать презентации по Педагогике
Презентация на тему "Воспитательная система МБОУ «Каратузская СОШ»" - скачать презентации по Педагогике Турнир новичка 2015-16-01
Турнир новичка 2015-16-01 Идентификация контролируемых товаров и технологий Статья 24. Идентификация контролируемых товаров и технологий  
Идентификация контролируемых товаров и технологий Статья 24. Идентификация контролируемых товаров и технологий   История становления и развития социологии
История становления и развития социологии Оптимизация и измерение производительности
Оптимизация и измерение производительности Основные термины и определения. Метод сечений
Основные термины и определения. Метод сечений Греческое: искусство украшать. Греческое: искусство украшать.
Греческое: искусство украшать. Греческое: искусство украшать. Theory of International Relations
Theory of International Relations фракталы, нелинейная динамика
фракталы, нелинейная динамика Основы SQL. Описание отношений, доменов, ограничений целостности, представлений данных.
Основы SQL. Описание отношений, доменов, ограничений целостности, представлений данных.