Нормальный закон распределения

План лекции:

Закономерности нормального распределения
Кривая нормального распределения и ее характеристики
Интервальные оценки
Генеральная и

Нормальный закон распределения случайных величин

Нормальное распределение возникает тогда, когда на

ЗАКОНОМЕРНОСТИ НОРМАЛЬНОГО РАСПРЕДЕЛЕНИЯ:

Параметр μ характеризует математическое ожидание (среднее арифметическое) случайной величины,

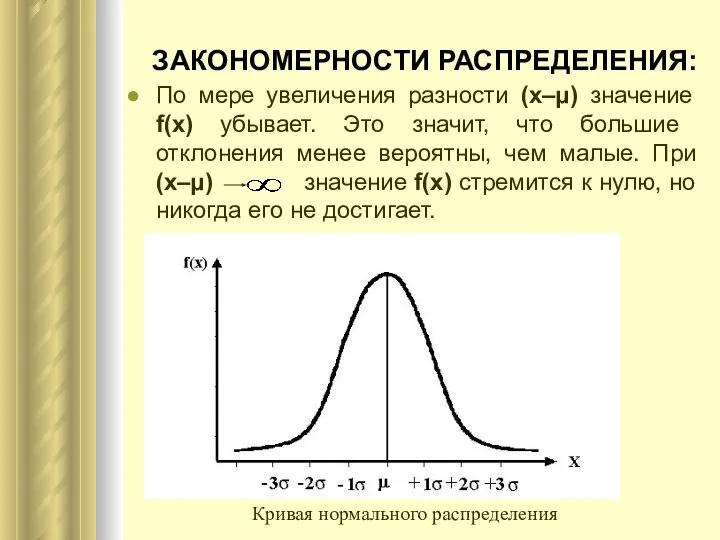
ЗАКОНОМЕРНОСТИ РАСПРЕДЕЛЕНИЯ:

По мере увеличения разности (x–μ) значение f(x) убывает. Это значит,

Функция распределения вероятностей:

Функция плотности распределения вероятностей:

Вероятность попадания значения случайной величины в интервал от а до

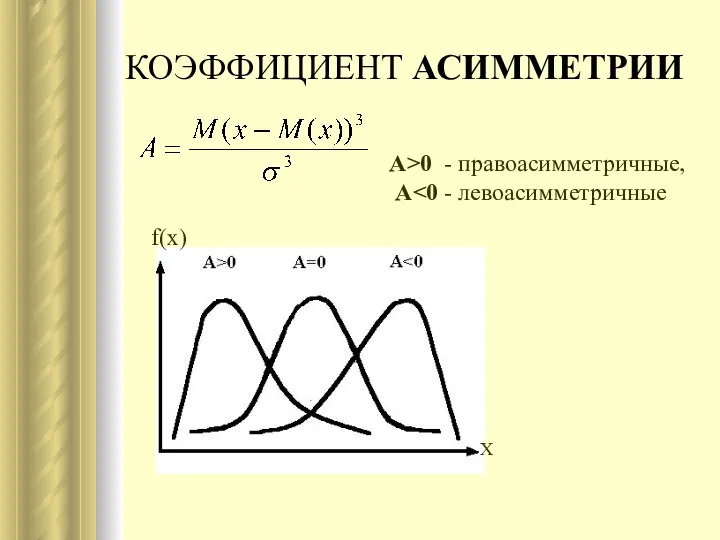
КОЭФФИЦИЕНТ АСИММЕТРИИ

А>0 - правоасимметричные,
А<0 - левоасимметричные

f(x)

X

ПОКАЗАТЕЛЬ ЭКСЦЕССА

f(x)

Х

Интервальные оценки

нормированное отклонение

х – μ=σt

1σ – 68,3%;

2σ – 95,5%;

3σ

Доверительные вероятности и доверительные интервалы

Вероятности 0,95 и 0,99 (95% и 99%)

Генеральная и выборочные совокупности

Наиболее общую совокупность, подлежащих изучению объектов называют генеральной.
Выборка

Сравнительная характеристика

Средняя квадратическая ошибка (стандартная ошибка)

s

σ

Среднее квадратическое отклонение

μ

Математическое
ожидание

Выборочная

Генеральная

Совокупность

Характеристики

значение генеральной средней
с

Сравнение теоретических и эмпирических распределений

Нулевая гипотеза. Согласно этой гипотезе первоначально принимается,

Средние квадратические ошибки sА (асимметрии) и sЕ (эксцесса)

Для достаточно большой

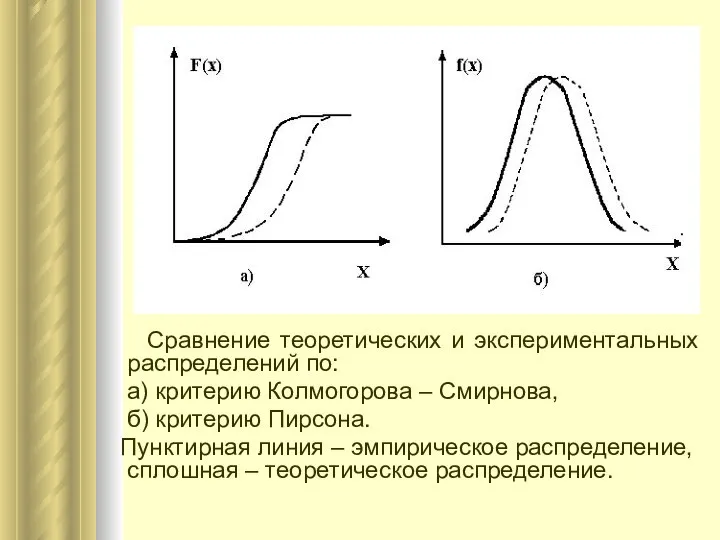
Сравнение теоретических и экспериментальных распределений по:
а) критерию Колмогорова

Критерий Пирсона

где mi – экспериментальные частоты попадания значения случайной величины

Число степеней свободы – это общее число величин, по которым вычисляются

Основные этапы исследования:

Сгруппировать исследуемый ряд по классам. Подсчитать середины интервалов и