Содержание
- 2. Размещения Теорема: число размещений из n по m равно Размещением из n элементов по m называется
- 3. 1) Студенты изучают 6 различных дисциплин. Если ежедневно в расписание включается по три дисциплины, то сколькими
- 4. Перестановки Перестановкой из n элементов называется любое упорядоченное множество, в которое входят по одному разу все
- 5. Записать все возможные перестановки для чисел 3,5,7 3,5,7 ; 3,7,5 ; 5,3,7 ; 5,7,3 ; 7,3,5
- 6. Сочетания Сочетанием из n элементов по m называется любое подмножество из m элементов, которые принадлежат множеству,
- 7. 1) Имеется 10 белых и 5 черных шаров. Сколькими способами можно выбрать 7 шаров , что
- 8. Правило умножения Если требуется выполнить одно за другим какие то K действий при чем 1 действие
- 9. Правило сложения Если два действия взаимно исключают друг друга, при чем одно из них можно выполнить
- 10. Основные понятия События А и В называются несовместными, если в результате данного испытания появление одного из
- 11. Пусть А и В - события, связанные с каким-либо опытом. ОПЕРАЦИИ НАД СОБЫТИЯМИ Пример: выпадение герба
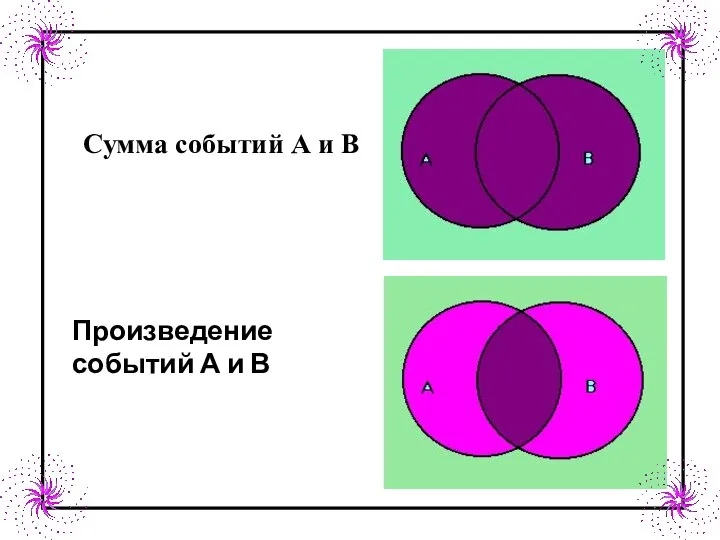
- 14. Сумма событий А и В Произведение событий А и В
- 15. Событие А - попадание при первом выстреле, событие В - попадание при втором выстреле. Событие А+В
- 16. Пусть событие А1 - попадание в цель при первом выстреле; Ā1 - промах при первом выстреле;
- 17. Событие В выразится в виде комбинации событий А и Ā:
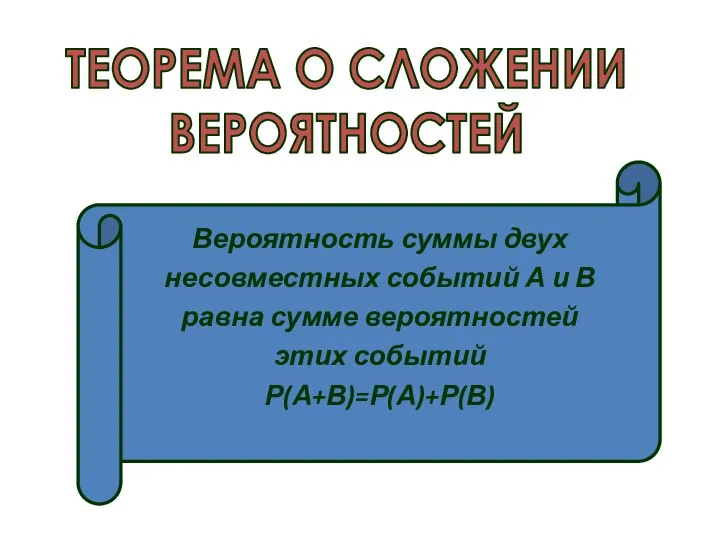
- 18. ТЕОРЕМА О СЛОЖЕНИИ ВЕРОЯТНОСТЕЙ Вероятность суммы двух несовместных событий А и В равна сумме вероятностей этих
- 19. Пусть все возможные исходы опыта сводятся к n случаям, из которых m случаев благоприятны событию А,
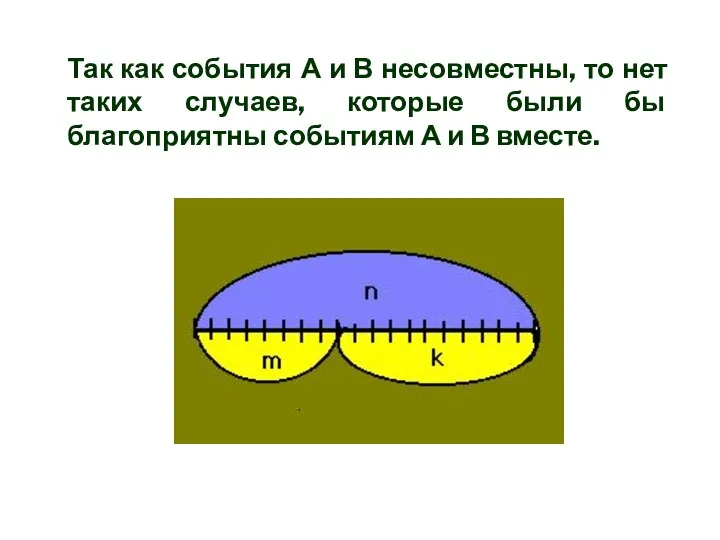
- 20. Так как события А и В несовместны, то нет таких случаев, которые были бы благоприятны событиям
- 21. Следовательно, событию А+В будет благоприятно m+k случаев.
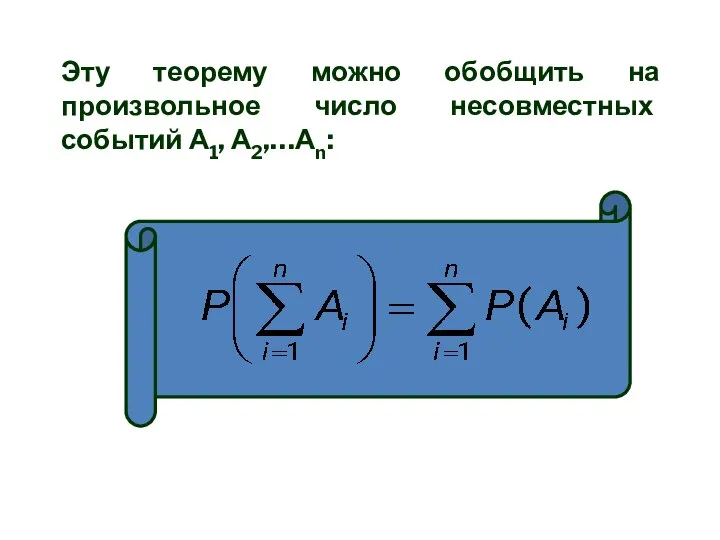
- 22. Эту теорему можно обобщить на произвольное число несовместных событий А1, А2,…Аn:
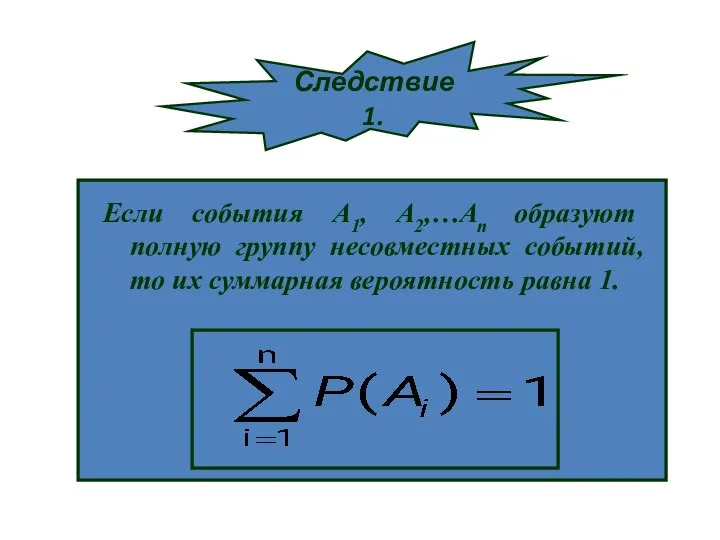
- 23. Если события А1, А2,…Аn образуют полную группу несовместных событий, то их суммарная вероятность равна 1. Следствие
- 24. Так как события А1, А2,…Аn образуют полную группу, то появление в опыте хотя бы одного из
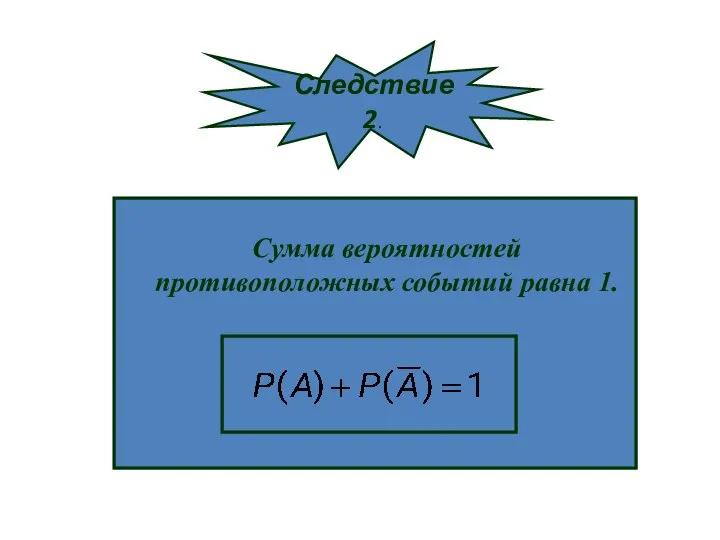
- 25. Сумма вероятностей противоположных событий равна 1. Следствие 2.
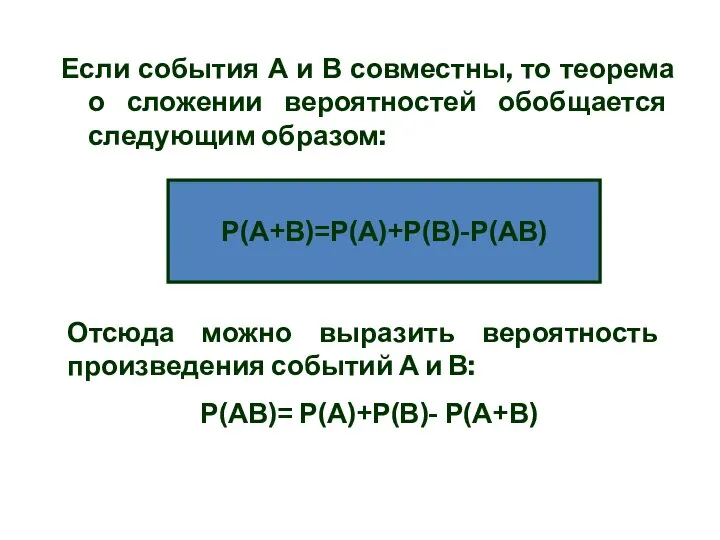
- 26. Если события А и В совместны, то теорема о сложении вероятностей обобщается следующим образом: Р(А+В)=Р(А)+Р(В)-Р(АВ) Отсюда
- 27. Пример 1.
- 28. События А и В будут совместными. Поэтому по теореме о сложении вероятностей вероятность того, что наугад
- 29. Р(А)=0.4, Р(В)=0.2, Р(АВ)=0.1 Следовательно,
- 30. Пример 2. Молодой человек рассматривает три возможности уклониться от службы в армии. Во-первых, он может поступить
- 31. Решение. Пусть событие А заключается в том, что молодой человек поступит в ВУЗ, событие В -
- 32. Так как Р(А)=0.5 Р(В)=0.2 Р(С)=0.01 то Р(А+В+С)=0.5+0.2+0.01=0.7
- 33. Теорема умножения вероятностей. Условная вероятность Условной вероятностью называется вероятность события В, вычисленная в предположении, что событие
- 34. Теорема умножения вероятностей. Условная вероятность Вероятность совместного наступления конечного числа событий равна произведению вероятности одного из
- 35. Формула полной вероятности является следствием теорем о сложении и умножении вероятностей. Пусть требуется определить вероятность события
- 36. По теореме об умножении вероятностей Отсюда вытекает формула полной вероятности: Так как гипотезы Н1,Н2…Нn несовместны, то
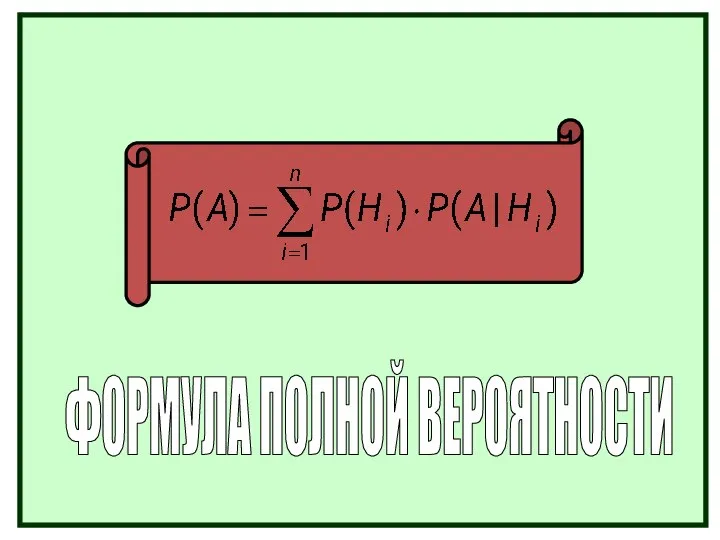
- 37. Формула полной вероятности. Вероятность события А, которое может наступить только при условии появления одного из событий
- 38. ФОРМУЛА ПОЛНОЙ ВЕРОЯТНОСТИ
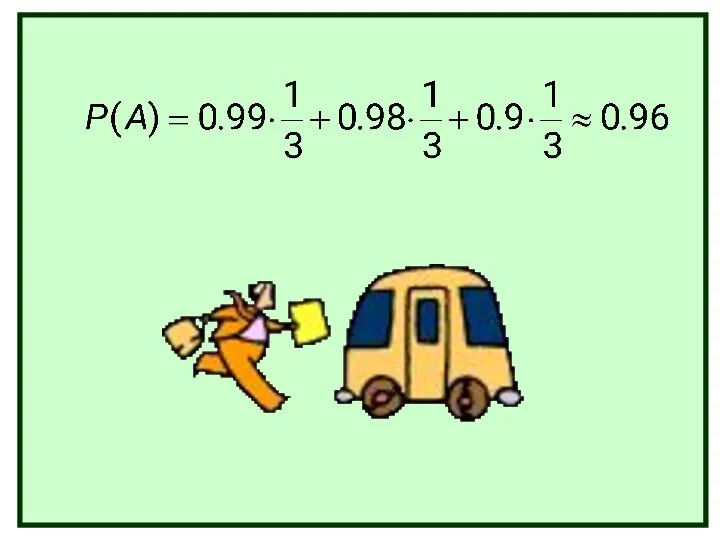
- 39. Студент, выйдя из дома за 30 минут до начала занятий, может приехать в институт автобусом, троллейбусом
- 40. Н1- студент поехал автобусом; Н2- студент поехал троллейбусом; Н3- студент поехал трамваем. Чтобы использовать формулу полной
- 41. Так как гипотезы образуют полную группу событий, то суммарная вероятность всех гипотез равна 1. По условию
- 43. Формула полной вероятности. Рассмотрим события В1, В2, В3,…,Вn которые образуют полную группу событий и при наступлении
- 44. ТЕОРЕМА ГИПОТЕЗ (ФОРМУЛА БАЙЕСА) Пусть имеется полная группа несовместных гипотез Н1,Н2…Нn . Вероятности этих гипотез до
- 45. Определим условные вероятности каждой из гипотез Р(Нi/А). По теореме об умножении вероятностей: Отсюда По формуле полной
- 46. ФОРМУЛА БАЙЕСА
- 47. Формула Байеса Рассмотрим событие А которое может наступить при условии появления одного из несовместных событий, В1,
- 48. Перед экзаменом студент с равной вероятностью может спрятать шпаргалку в одно из трех мест: в ботинок,
- 49. Н1- достал шпаргалку из ботинка; Н2- достал шпаргалку из кармана; Н3- достал шпаргалку из рукава. Событие
- 50. Т.е. требуется определить условную вероятность первой гипотезы, при условии, что событие А имело место. Для этого
- 51. Тогда Условные вероятности события А для каждой из гипотез даны по условию задачи: Р(А|Н1)=0.4; Р(А|Н2)=0.6; Р(А|Н3)=0.55
- 52. ПРИМЕР 2. Статистика запросов кредитов в банке: 10 % - государственные органы, 30 % - банки,
- 53. Гипотезами в этой задаче будут: Н1- кредит взял государственный орган; Н2- кредит взял банк; Н3- кредит
- 54. Условные вероятности события А для каждой из гипотез даны в задаче: Р(А|Н1)=0.01; Р(А|Н2)=0.05; Р(А|Н3)=0.2. Тогда: Вероятность
- 55. Формула Бернулли Вероятность того что в n независимых испытаниях в каждом из которых вероятность появления события
- 56. Если производится n независимых опытов, в каждом из которых событие А появляется с вероятностью Р, то
- 57. Известно, если монета упадет орлом, студент идет пить пиво, если монета упадет решкой – студент идет
- 58. Решение: Тогда вероятность противоположного события составит q=3/4. По формуле Бернулли находим вероятность того, что при 5
- 59. Чтобы найти вероятность того, что при 5 бросаниях хотя бы один раз монета повиснет в воздухе,
- 60. Тогда вероятность искомого события составит
- 61. Асимптотические формулы Если число испытаний велико, то использование формулы Бернулли будет нецелесообразным в силу необходимости выполнения
- 63. Скачать презентацию



















































 Личное резюме. Собеседование при приеме на работу. 1. Правила написания резюме. 2. Разговор по телефону с потенциальным работо
Личное резюме. Собеседование при приеме на работу. 1. Правила написания резюме. 2. Разговор по телефону с потенциальным работо Презентация на тему Свойство металлов и сплавов 6 класс
Презентация на тему Свойство металлов и сплавов 6 класс  Технико-юридические приемы и правила подготовки нормативного правового акта
Технико-юридические приемы и правила подготовки нормативного правового акта Презентация "Сырьевые товары. Сущность и формы и особенности торговли сырьевой продукцией" - скачать презентации по Экономик
Презентация "Сырьевые товары. Сущность и формы и особенности торговли сырьевой продукцией" - скачать презентации по Экономик American football
American football Безопасность человека в ЧС техногенного характера
Безопасность человека в ЧС техногенного характера Новые понятия в старой оболочке Работа с понятийным аппаратом на уроках обществознания Учитель истории и обществоведения МОУ «С
Новые понятия в старой оболочке Работа с понятийным аппаратом на уроках обществознания Учитель истории и обществоведения МОУ «С Удержание персонала: подходы и пути решения Игорь Радченко, менеджер по работе с персоналом, DHL International 30 Марта 2006 года
Удержание персонала: подходы и пути решения Игорь Радченко, менеджер по работе с персоналом, DHL International 30 Марта 2006 года Презентация на тему "спинной мозг" - скачать презентации по Медицине
Презентация на тему "спинной мозг" - скачать презентации по Медицине Химическая связь
Химическая связь Алгоритмическая структура «Цикл»
Алгоритмическая структура «Цикл» Президент Грузии
Президент Грузии Презентация на тему "Портфоліо учнів 2-Б класу Жидачівської ЗОШ №2" - скачать презентации по Педагогике
Презентация на тему "Портфоліо учнів 2-Б класу Жидачівської ЗОШ №2" - скачать презентации по Педагогике Мозговой штурм
Мозговой штурм Аттестационная работа. Организация этнографической экспедиции школьников по изучению темы «Народная художественная культуры»
Аттестационная работа. Организация этнографической экспедиции школьников по изучению темы «Народная художественная культуры» Круглый стол по уголовному праву
Круглый стол по уголовному праву Как празднуют новый год в Италии
Как празднуют новый год в Италии устройства ввода-вывода
устройства ввода-вывода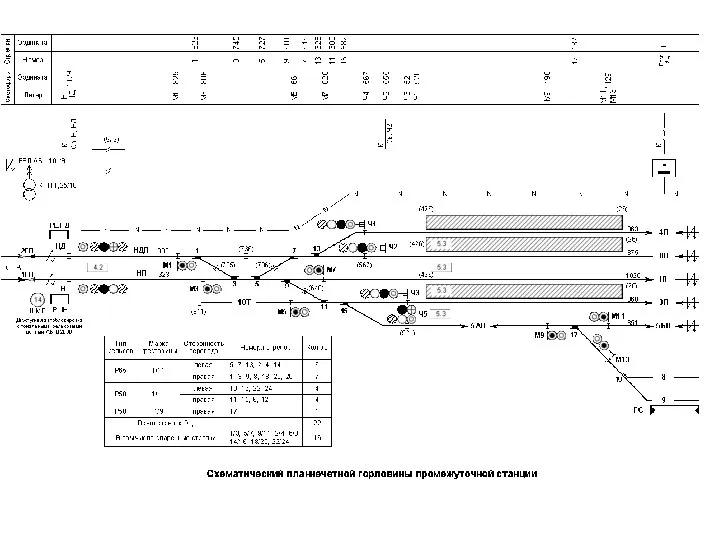 Структурная схема централизации
Структурная схема централизации Образы пушкинской прозы и поэзии в книжных иллюстрациях
Образы пушкинской прозы и поэзии в книжных иллюстрациях Примитивизм
Примитивизм  Цветы глазами художников
Цветы глазами художников Основы конституционного права РФ. Тема 5
Основы конституционного права РФ. Тема 5 Нормы права и нормативно-правовые акты. Источники российского права. Отрасли права. (Лекция 3)
Нормы права и нормативно-правовые акты. Источники российского права. Отрасли права. (Лекция 3) Многообразие культур и способы их изучения
Многообразие культур и способы их изучения ДЕЛОВАЯ ИГРА Редакция Мы будем помнить каждый миг, Наш лучший друг – родной язык! Невозможно стать культурным Без р
ДЕЛОВАЯ ИГРА Редакция Мы будем помнить каждый миг, Наш лучший друг – родной язык! Невозможно стать культурным Без р Международные правовые акты
Международные правовые акты Costum naţional Сhina
Costum naţional Сhina