Содержание
- 2. 6.1 Интуитивное понятие об алгоритме Интуитивное понятие алгоритма. Алгоритм – это правило, сформированное на некотором языке
- 3. Правила описания алгоритмов: Понятность для исполнителя Массовость (т.е. допустимость для него всех предложений языка исходных данных)
- 4. Алгоритм применим к допустимому исходному данному, если с его помощью, отправляясь от этого исходного данного, можно
- 5. Поскольку требование завершения алгоритмического процесса за конечное число шагов не учитывает реальных возможностей, связанных с затратами
- 6. Об источниках алгоритмов: Практика; научная теория; совокупность накопленных алгоритмов; изобретательность разработчика.
- 7. 6.2 Три типа алгоритмических моделей Различный выбор исходных средств формализации приводит к моделям алгоритмов разного вида.
- 8. Первый тип Связывает понятие алгоритма с вычислениями и числовыми функциями. Наиболее развитая и изученная модель этого
- 9. Второй тип Основан на представлении об алгоритме как о некотором детерминированном устройстве, способном выполнять в каждый
- 10. Третий тип Это преобразование слов в произвольных алфавитах, в которых элементарными операциями являются подстановки, т.е. замена
- 11. Тезис Чёрга Класс задач, решаемых в любой из этих формальных моделей, и есть класс всех задач,
- 12. Примеры. Задача о квадратуре круга. Требуется найти алгоритм построения с помощью циркуля и линейки квадрата, равновеликого
- 13. Примеры. Задача удвоения куба. Найти алгоритм, позволяющий на стороне любого куба с помощью циркуля и линейки
- 14. Вторая причина разработки теории алгоритмов – необходимость обоснования математики, поскольку появления антиномий привели к тому, что
- 15. Пример Актуально бесконечное множество. Расходуя ограниченное количество ресурсов на каждом шаге, имеющим фиксированную длительность, построить такое
- 16. 6.3 Кризис теории множеств антиномии. Выводы из антиномий. До середины XIX века никто не сомневался в
- 17. На втором Международном Математическом Конгрессе было заявлено, что теперь в математике остались только целые числа и
- 18. Две теории Кантора из теории множеств Кардинальное число множества М называется его мощностью и обозначается m.
- 19. Парадокс Кантора. Пусть М множество всех множеств обозначим его кардинальное число буквой m. В силу теоремы
- 20. Парадокс Рассела (парадокс брадобрея). Один из солдат оказался по профессии парикмахером, узнав об этом командир приказал
- 21. Открытие антиномий потрясло математику и математиков, как землетрясение. Нужно сказать, что математики поразному отреагировали на это
- 22. 6.4 Машины Тьюринга как модели алгоритмов В 1937г. английский математик Тьюринг опубликовал работу в которой он
- 23. Машина состоит из бесконечной в обе стороны ленты, разбитой на ячейки, и рабочей головки. Машина работает
- 24. Основной частью машины является логический блок, который работает следующим образом. В каждый момент времени рабочая головка
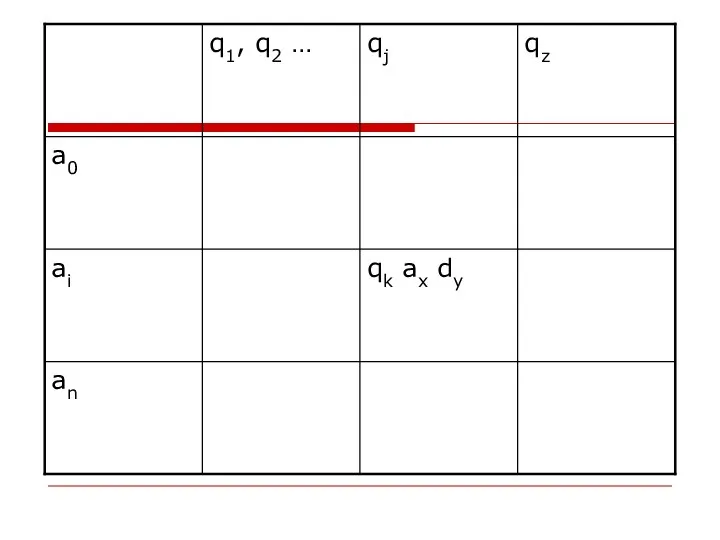
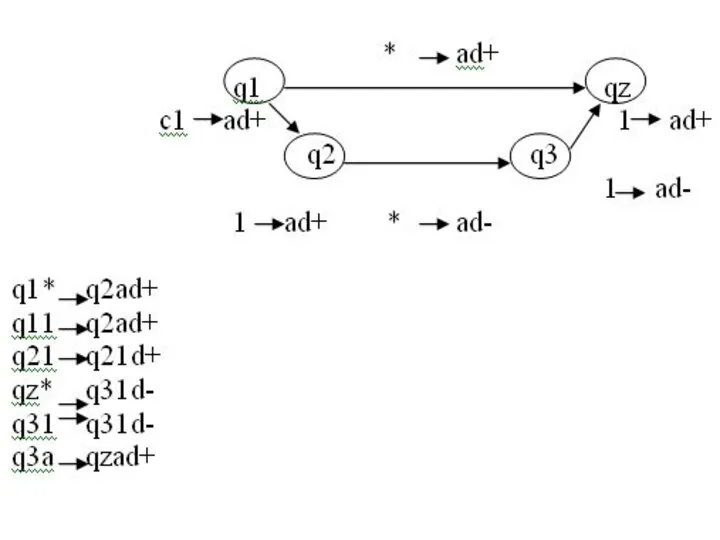
- 25. Т.о. работа МТ задается системой команд вида: qj*ai-qk*ax*dy Все случаи сочетания qj и ai для разных
- 26. Если головка в состоянии qj читаем символ ai, то в следующий момент она записывает в эту
- 28. Примеры построения машин Тьюринга Постороить машину Тьюринга, реализущую. «сложение» чисел. В машине Тюринга все числа представляются
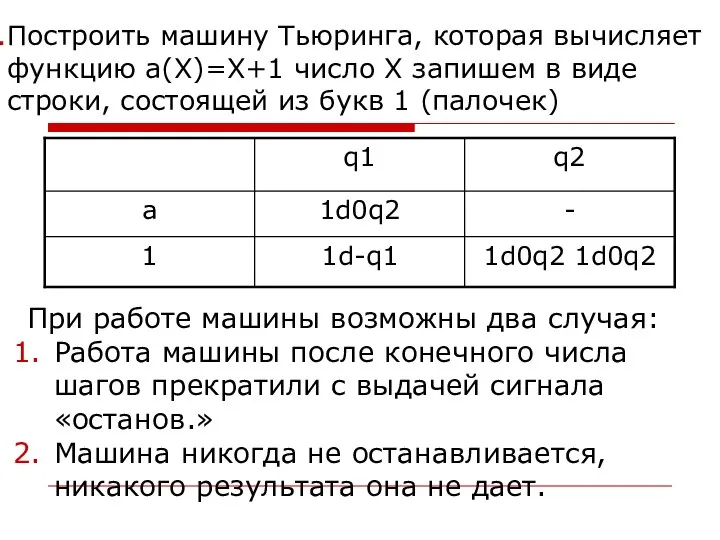
- 30. Построить машину Тьюринга, которая вычисляет функцию а(Х)=Х+1 число Х запишем в виде строки, состоящей из букв
- 31. В первом случае говорят, что машина применила к исходному данному, во втором – не применима. Соответствия
- 32. Тезис Тьюринга: Любая вычислимая функция вычислимая по Тьюрингу, или всякий алгоритм может быть реализован машиной Тьюринга.
- 33. Проблема остановки: Можно ли построить машину То такую что для любой машины Тк любых исходных данных
- 35. Скачать презентацию





























 Христианская надежда. Молитва Господня
Христианская надежда. Молитва Господня Культура Руси в период ордынского владычества
Культура Руси в период ордынского владычества Взаимодействие природных и городских ландшафтов в градостроительстве
Взаимодействие природных и городских ландшафтов в градостроительстве Манипулирование данными в R
Манипулирование данными в R Как празднуют Новый год в разных странах
Как празднуют Новый год в разных странах АНИМАЦИЯ СИМВОЛОВ в среде Flash
АНИМАЦИЯ СИМВОЛОВ в среде Flash ALBRECHT DÜRER (1471-1528)
ALBRECHT DÜRER (1471-1528)  Традиции и обряды русского народа
Традиции и обряды русского народа Атрибуты deftemplate
Атрибуты deftemplate Складаємо робота. Stickers
Складаємо робота. Stickers Процесс становления гражданственности молодежи как направление государственной молодежной политики
Процесс становления гражданственности молодежи как направление государственной молодежной политики Системы программирования. Интегрированные среды разработки. Системы контроля версий
Системы программирования. Интегрированные среды разработки. Системы контроля версий Расстановка фигур
Расстановка фигур Ақпарат алмасудың магистралдық (шиналық) жүйесі. Интерфейстер. Цифрлы техниканың есте сақтау құрылғысы
Ақпарат алмасудың магистралдық (шиналық) жүйесі. Интерфейстер. Цифрлы техниканың есте сақтау құрылғысы РАДИОТЕХНИЧЕСКИЕ ЦЕПИ И СИГНАЛЫ 6
РАДИОТЕХНИЧЕСКИЕ ЦЕПИ И СИГНАЛЫ 6 Элементы машиноведения. Составные части машин
Элементы машиноведения. Составные части машин Выполнил Студент 1 курса Группы Юб02/1403 Кудрявцев Алексей
Выполнил Студент 1 курса Группы Юб02/1403 Кудрявцев Алексей  Учитель начальных классов МБОУ СОШ №39 города Дзержинска Нижегородской области Парфёнова Татьяна Викторовна
Учитель начальных классов МБОУ СОШ №39 города Дзержинска Нижегородской области Парфёнова Татьяна Викторовна Трудовой договор. Коллективный договор
Трудовой договор. Коллективный договор Аппаратная часть компьютерной системы. Схема простого компьютера
Аппаратная часть компьютерной системы. Схема простого компьютера Спасение через веру во Христа. Правильное отношение к смерти и подготовка к ней
Спасение через веру во Христа. Правильное отношение к смерти и подготовка к ней Язык программирования Pascal. Линейные алгоритмы
Язык программирования Pascal. Линейные алгоритмы Корзина для хранения
Корзина для хранения Модульное тестирование с JUnit
Модульное тестирование с JUnit Презентация Срок временного хранения товаров. Операции с товарами, находящимися на временном хранении.
Презентация Срок временного хранения товаров. Операции с товарами, находящимися на временном хранении. Англия раннее Средневековье 5 параграф
Англия раннее Средневековье 5 параграф English in European integration
English in European integration Ефірний інтерфейс
Ефірний інтерфейс