Содержание
- 2. 4.1 Способы задания булевой функции Пусть х1, х2, ... , хn – некоторые булевы переменные, т.
- 3. При фиксации значений всех переменных получается набор значений переменных (х1, х2, ..., хn), задаваемый булевым вектором
- 4. Задание булевой функции f на булевом пространстве М делит его на две части: Mf1 – область,
- 5. Пример задания булевой функции от трех аргументов
- 6. Для задания булевой функции можно ограничиться перечислением элементов ее характеристического множества Mf1. Множество Mf1 задается булевой
- 7. Компактность представления характеристического множества Mf1 можно повысить, используя троичные векторы, компоненты которых могут принимать в качестве
- 8. Булевы векторы а = (а1, а2, … , аn) и b = (b1, b2, … ,
- 9. Троичная матрица эквивалентна булевой матрице, получаемой из нее заменой каждой троичной строки на представляемую ею совокупность
- 10. Такой способ задания булевой функции называют еще интервальным. Представление булевой функции троичной матрицей не однозначно, т.
- 11. Векторное задание булевой функции представляет собой булев вектор, компоненты которого соответствуют наборам значений аргументов. Эти наборы
- 12. Если значения булевой функции определены для всех 2n наборов значений вектора x, она называется полностью определенной,
- 13. 4.2 Элементарные булевы функции и алгебраические формы Рассматривая векторную форму задания булевой функции, легко определить число
- 14. Функция f(х1, х2, ... , хn) существенно зависит от аргумента хi, если f(х1, х2, ... ,
- 15. Элементарными булевыми функциями являются функции от одной и двух переменных. Число функций от одной переменной равно
- 16. Функция f1 также является тривиальной, любое ее значение совпадает со значением аргумента: f1(x) = x. Нетривиальной
- 17. В таблице приведены все булевы функции fi (х1, х2) от двух аргументов. В левом столбце показаны
- 18. Продолжение таблицы
- 38. Скачать презентацию



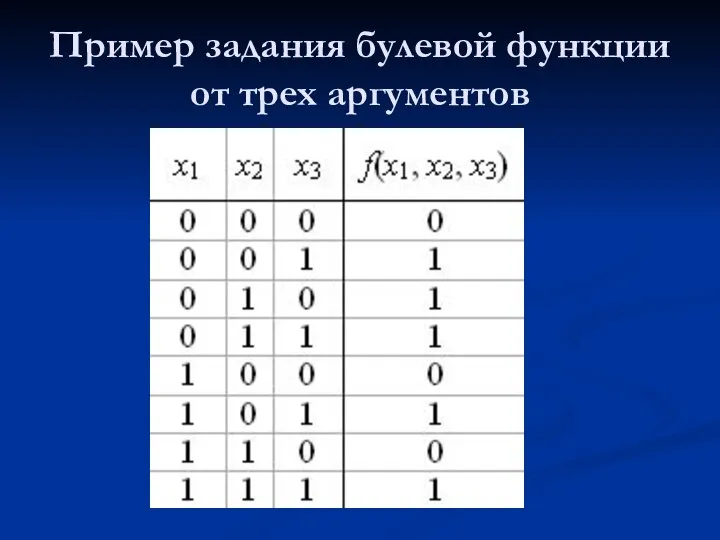































 Схема внешнего электроснабжения ОГР
Схема внешнего электроснабжения ОГР Осушение слабопроницаемых пород
Осушение слабопроницаемых пород "Призрак оперы" Гастон Леру
"Призрак оперы" Гастон Леру Загальна характеристика літератури зрілого Середньовічч
Загальна характеристика літератури зрілого Середньовічч Биомеханические основы физических качеств
Биомеханические основы физических качеств Презентация "Поведенческие аспекты контроля" - скачать презентации по Экономике
Презентация "Поведенческие аспекты контроля" - скачать презентации по Экономике Уральские промыслы
Уральские промыслы http://www.gilev.ru 1C:Предприятие 8
http://www.gilev.ru 1C:Предприятие 8 Презентация МЕМОРАНДУМ МЕЖДУ ПРАВИТЕЛЬСТВОМ СССР И ПРАВИТЕЛЬСТВОМ СОЕДИНЕННЫМИ ШТАТАМИ АМЕРИКИ О ВЗАИМОПОНИМАНИИ О СОТРУДНИЧЕС
Презентация МЕМОРАНДУМ МЕЖДУ ПРАВИТЕЛЬСТВОМ СССР И ПРАВИТЕЛЬСТВОМ СОЕДИНЕННЫМИ ШТАТАМИ АМЕРИКИ О ВЗАИМОПОНИМАНИИ О СОТРУДНИЧЕС Астрофизика введение
Астрофизика введение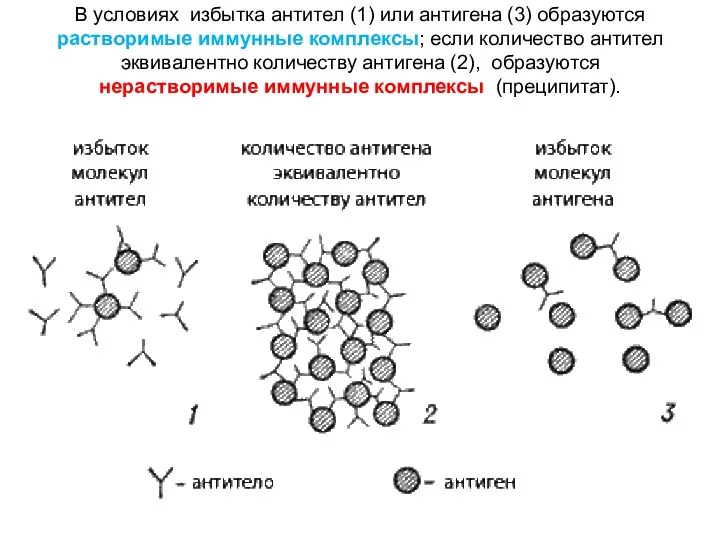 занятие антитела
занятие антитела Учитель: Ковшина Елена Владимировна, Всё о звуках
Учитель: Ковшина Елена Владимировна, Всё о звуках Предельная нестехиометрия в кристаллах
Предельная нестехиометрия в кристаллах Роль МО в формировании ценностной культуры учебного труда.
Роль МО в формировании ценностной культуры учебного труда. Теории происхождения права
Теории происхождения права Надежность диагностических тестов
Надежность диагностических тестов Словарные слова по теме «Экскурсия» (4 класс) Презентация ученика 4 «А» класса Белоусова Константина
Словарные слова по теме «Экскурсия» (4 класс) Презентация ученика 4 «А» класса Белоусова Константина Хирургия – область медицины, изучающая заболевания, которые лечатся при помощи оперативного (хирургического) метода. Материал п
Хирургия – область медицины, изучающая заболевания, которые лечатся при помощи оперативного (хирургического) метода. Материал п Erfassen von sozialräumen: sozialraumanalyse
Erfassen von sozialräumen: sozialraumanalyse Политология. Возникновение и предмет политологии
Политология. Возникновение и предмет политологии Паоло Уччелло (1397–1475) Качурова Юлия 10а класс ЯРГ 17.01.10
Паоло Уччелло (1397–1475) Качурова Юлия 10а класс ЯРГ 17.01.10 «Ручная вышивка как один из видов декоративно-прикладного искусства»
«Ручная вышивка как один из видов декоративно-прикладного искусства» Уравнения газовой динамики
Уравнения газовой динамики  Презентация на тему "От конфликта к культуре педагогического общения"
Презентация на тему "От конфликта к культуре педагогического общения" Массивы в Паскале. Одномерные массивы. (9 класс)
Массивы в Паскале. Одномерные массивы. (9 класс) О внесении изменений в Земельный кодекс Российской Федерации и отдельные законодательные акты Российской Федерации
О внесении изменений в Земельный кодекс Российской Федерации и отдельные законодательные акты Российской Федерации Введение в проектирование по предметной области (DDD)
Введение в проектирование по предметной области (DDD) ДЕНЬ РОЖДЕНИЯ БУКВЫ Ю
ДЕНЬ РОЖДЕНИЯ БУКВЫ Ю