Содержание
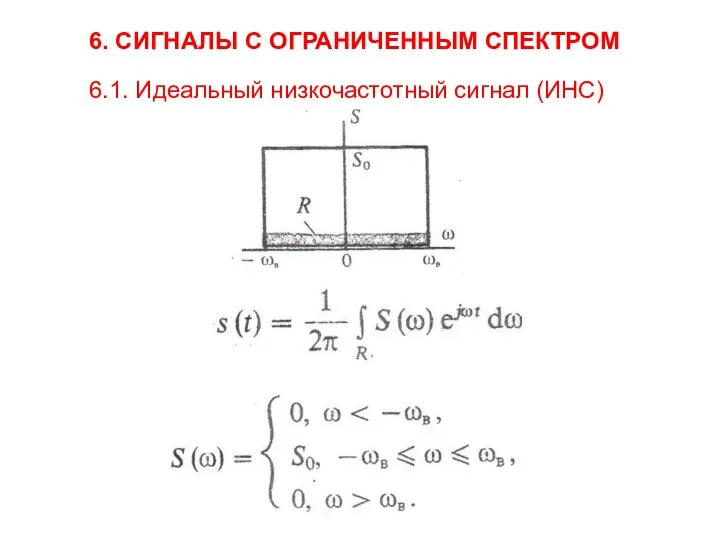
- 2. 6. СИГНАЛЫ С ОГРАНИЧЕННЫМ СПЕКТРОМ 6.1. Идеальный низкочастотный сигнал (ИНС)
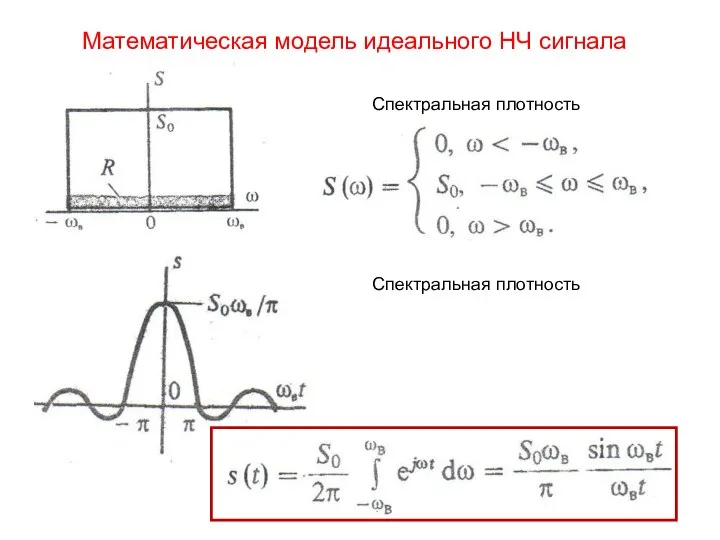
- 3. Математическая модель идеального НЧ сигнала Спектральная плотность Спектральная плотность
- 4. Математическая модель смещённого идеального НЧ сигнала График ИНС имеет вид осциллирующей кривой, четной относительно начала отсчета
- 5. Математическая модель смещённого идеального НЧ сигнала График ИНС имеет вид осциллирующей кривой, четной относительно начала отсчета
- 6. 6.2. Идеальный полосовой сигнал Наряду с высокочастотными осцилляциями на частоте наблюдается изменение во времени мгновенного значения
- 7. 6.3. Ортогональные сигналы с ограниченным спектром Два идеальных низкочастотных сигнала u(t) и v(t). Оба эти сигнала
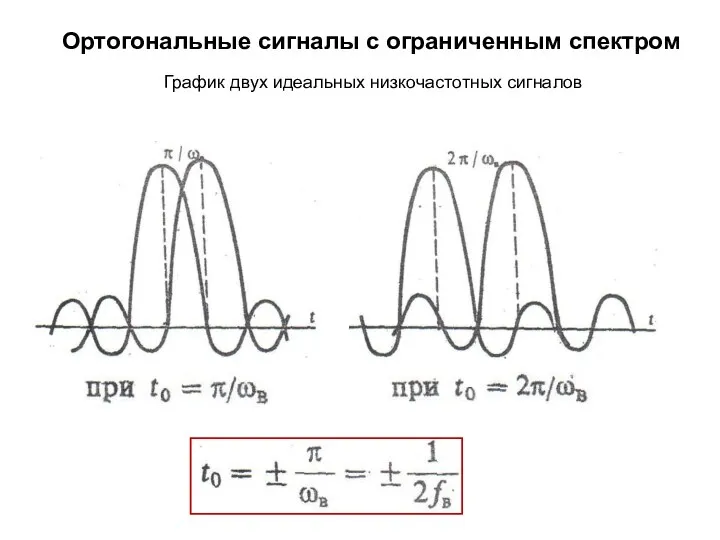
- 8. Ортогональные сигналы с ограниченным спектром График двух идеальных низкочастотных сигналов
- 9. 6.4. Теорема Котельникова Любые два сигнала с ограниченным спектром, принадлежащие семейству Базис Котельникова – бесконечный набор
- 10. Теорема Котельникова Ряд Котельникова Коэффициентами ряда служат скалярные произведения сигнала на соответствующую базисную функцию k-я отсчетная
- 11. Теорема Котельникова Ряд Котельникова Произвольный сигнал, спектр которого не содержит частот выше может быть полностью восстановлен,
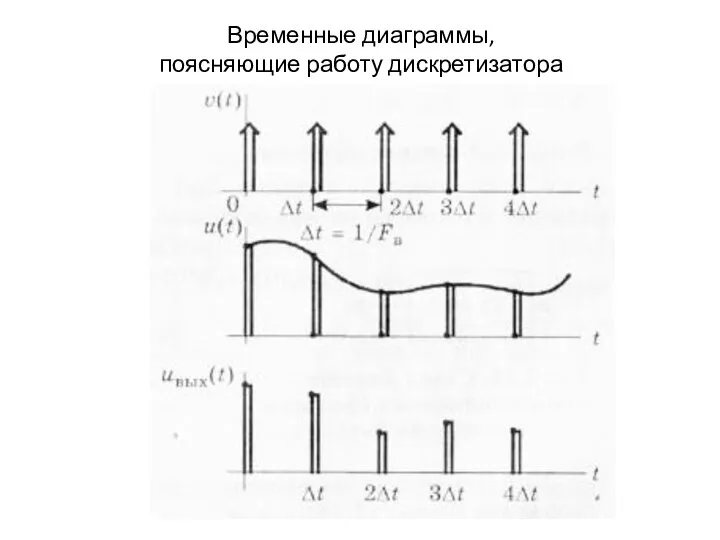
- 12. Временные диаграммы, поясняющие работу дискретизатора
- 13. Временные диаграммы, поясняющие восстановление сигнала
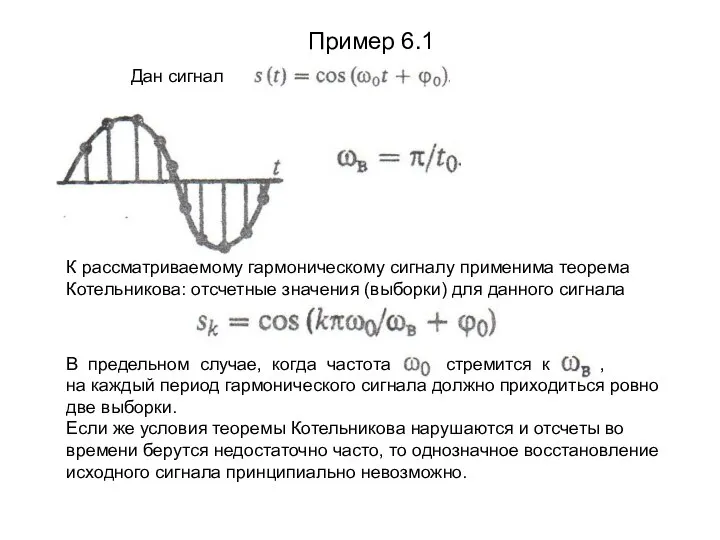
- 14. Пример 6.1 Дан сигнал К рассматриваемому гармоническому сигналу применима теорема Котельникова: отсчетные значения (выборки) для данного
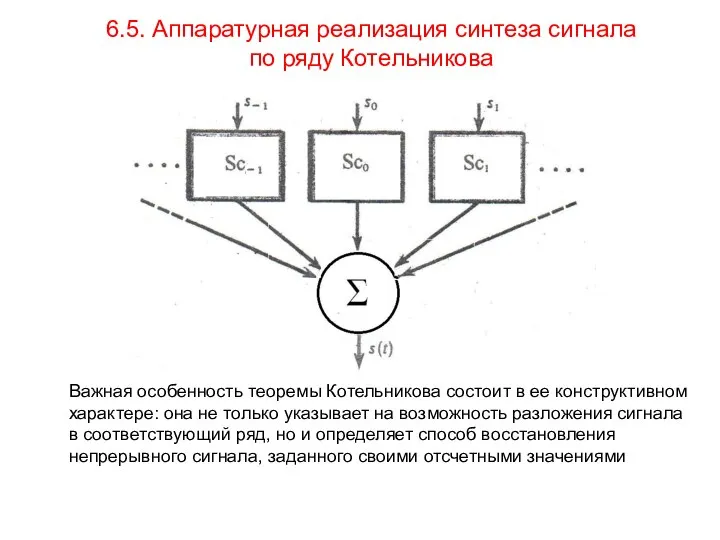
- 15. 6.5. Аппаратурная реализация синтеза сигнала по ряду Котельникова Важная особенность теоремы Котельникова состоит в ее конструктивном
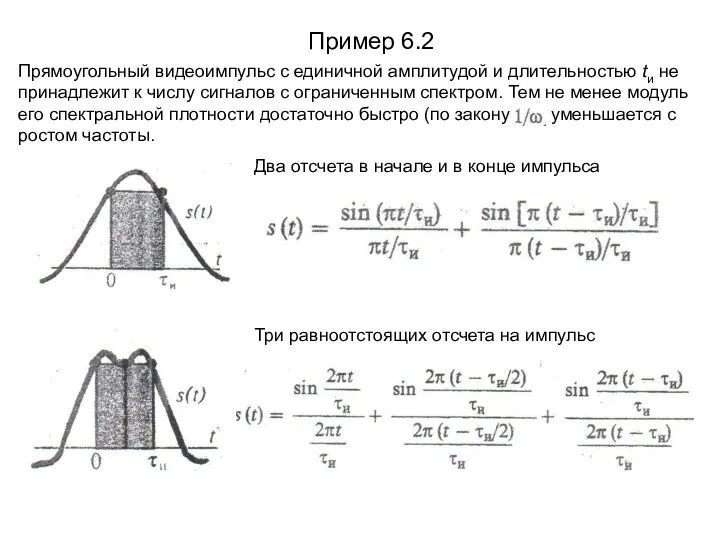
- 16. Пример 6.2 Прямоугольный видеоимпульс с единичной амплитудой и длительностью tи не принадлежит к числу сигналов с
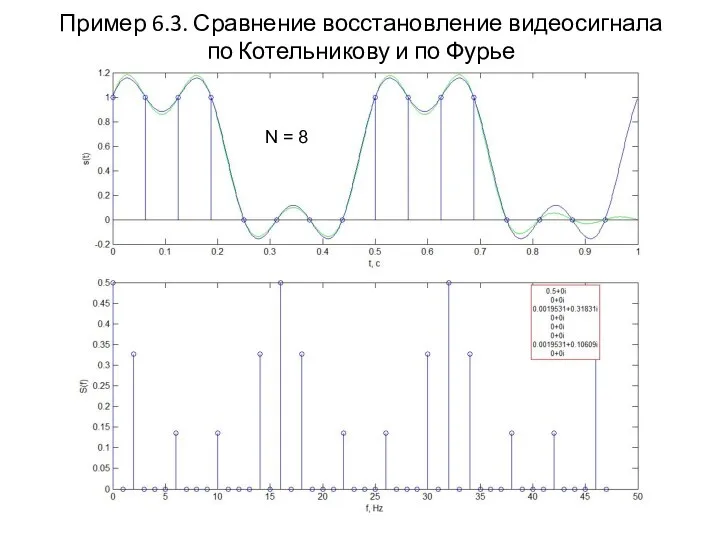
- 17. Пример 6.3. Сравнение восстановление видеосигнала по Котельникову и по Фурье N = 8
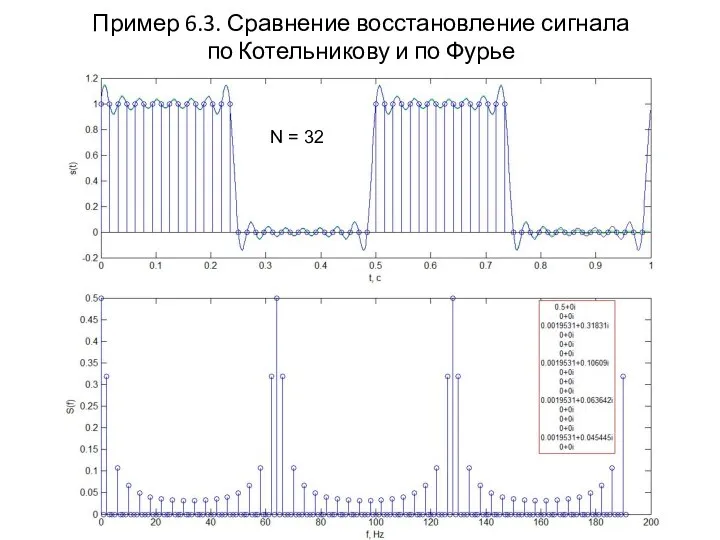
- 18. Пример 6.3. Сравнение восстановление сигнала по Котельникову и по Фурье N = 32
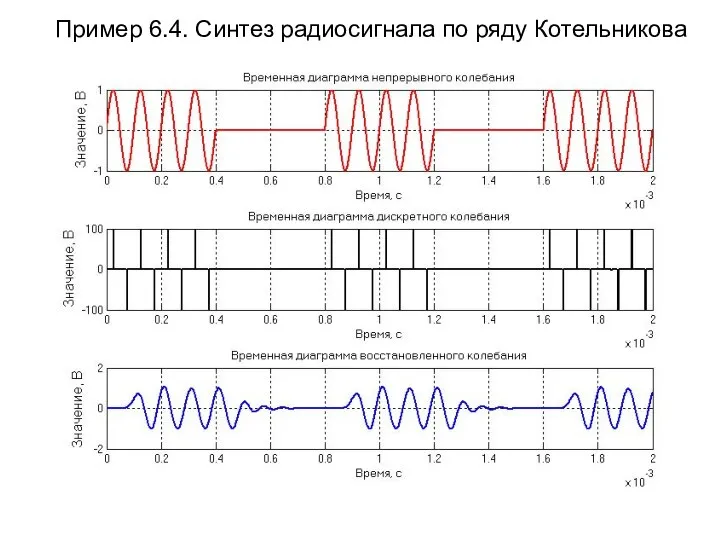
- 19. Пример 6.4. Синтез радиосигнала по ряду Котельникова
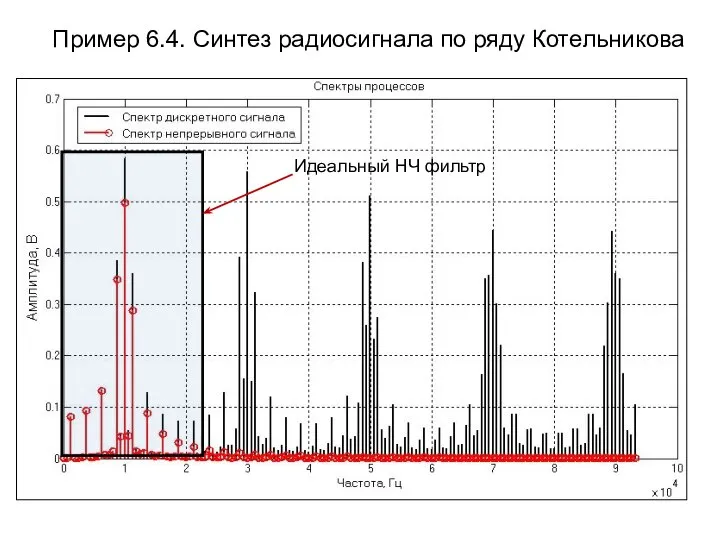
- 20. Пример 6.4. Синтез радиосигнала по ряду Котельникова Идеальный НЧ фильтр
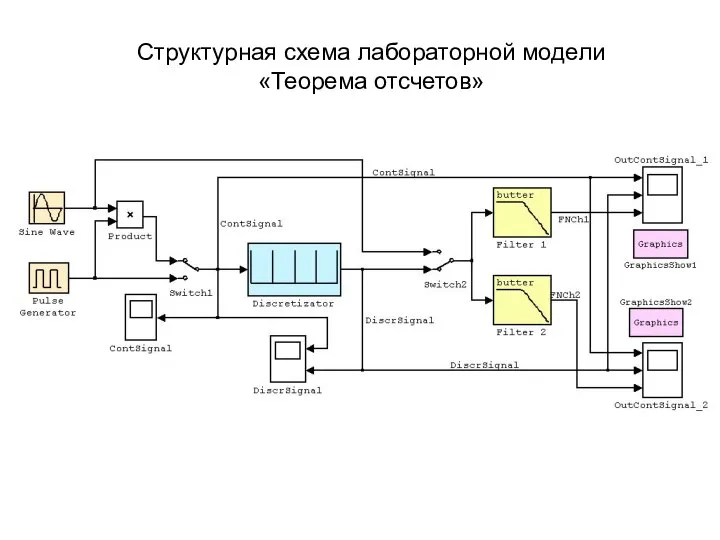
- 21. Структурная схема лабораторной модели «Теорема отсчетов»
- 22. 6.6. Оценка ошибки, возникающей при аппроксимации произвольного сигнала рядом Котельникова Произвольный сигнал можно представить суммой Если
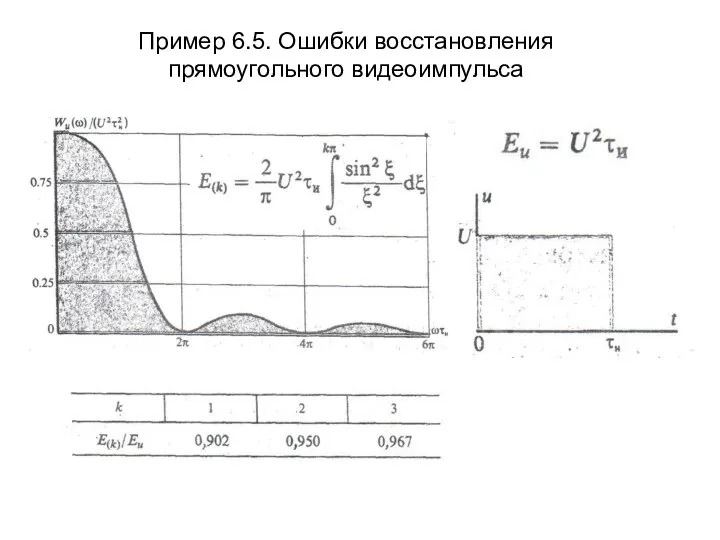
- 23. Пример 6.5. Ошибки восстановления прямоугольного видеоимпульса
- 25. Скачать презентацию









 Модель диагностики изменений Надлера и Ташмена Подготовили: студентки группы ДС04, Шунайлова Жанна и Епифанова Евгения
Модель диагностики изменений Надлера и Ташмена Подготовили: студентки группы ДС04, Шунайлова Жанна и Епифанова Евгения Этнический лоббизм
Этнический лоббизм Взвод в обороні
Взвод в обороні Plagiarism in Kazakhstan
Plagiarism in Kazakhstan Матч Украина-Латвия. Механизмы игры в футбол
Матч Украина-Латвия. Механизмы игры в футбол Презентация "Маэстро Гергиев - артист мира" - скачать презентации по МХК
Презентация "Маэстро Гергиев - артист мира" - скачать презентации по МХК Уголок психологической разгрузки «Маленькая страна» в подготовительной к школе группе № 12 Воспитатели: Алексеева Ольга Вла
Уголок психологической разгрузки «Маленькая страна» в подготовительной к школе группе № 12 Воспитатели: Алексеева Ольга Вла Казақстан ремпубликасынын конституциясы
Казақстан ремпубликасынын конституциясы Презентация "Питер Пауль Рубенс" - скачать презентации по МХК
Презентация "Питер Пауль Рубенс" - скачать презентации по МХК Надёжность оснований и строительных конструкций
Надёжность оснований и строительных конструкций Дисциплинированность - важнейшее качество личности военнослужащего внутренних войск МВД республики Беларусь
Дисциплинированность - важнейшее качество личности военнослужащего внутренних войск МВД республики Беларусь 4998f61117d196c76158f16d93ed1237
4998f61117d196c76158f16d93ed1237 Політичні конфлікти
Політичні конфлікти Презентация Понятие и значение института реабилитации в уголовном судопроизводстве. Основания и условия реабилитации.
Презентация Понятие и значение института реабилитации в уголовном судопроизводстве. Основания и условия реабилитации. ПАТОЛОГИЯ ЭНДОКРИННОЙ СИСТЕМЫ
ПАТОЛОГИЯ ЭНДОКРИННОЙ СИСТЕМЫ Лучевая диагностика заболеваний органов дыхания Основные заболевания Часть 1 Автор к.м.н. А.В.Шумаков
Лучевая диагностика заболеваний органов дыхания Основные заболевания Часть 1 Автор к.м.н. А.В.Шумаков  Профориентация в русле ФГОС нового поколения. Качурина Елена Юрьевна, педагог-психолог ГОУ СОШ № 328
Профориентация в русле ФГОС нового поколения. Качурина Елена Юрьевна, педагог-психолог ГОУ СОШ № 328 Цифровое меню для ресторанов Subway. Специальное предложение
Цифровое меню для ресторанов Subway. Специальное предложение Механические характеристики электродвигателей постоянного тока
Механические характеристики электродвигателей постоянного тока Автомат Уилкса. Микропрограммное устройство
Автомат Уилкса. Микропрограммное устройство  Презентация Источники экологического права. Нормы экологического права
Презентация Источники экологического права. Нормы экологического права  Принцип действия радиотелефонной связи Радиовещание и телевидение .ppt
Принцип действия радиотелефонной связи Радиовещание и телевидение .ppt Судебно-медицинская экспертиза при повреждениях от воздействия тупых орудий
Судебно-медицинская экспертиза при повреждениях от воздействия тупых орудий Быстрый путь от стартапа до бизнеса 29 февраля 2012 Уральская Интернет Неделя
Быстрый путь от стартапа до бизнеса 29 февраля 2012 Уральская Интернет Неделя История Мезоамерика
История Мезоамерика  Государственное бюджетное дошкольное образовательное учреждение детский сад №27 Пушкинского района г.Санкт-Петербурга Реализа
Государственное бюджетное дошкольное образовательное учреждение детский сад №27 Пушкинского района г.Санкт-Петербурга Реализа Измерение аберраций оптических систем
Измерение аберраций оптических систем Кадровое делопроизводство
Кадровое делопроизводство