Содержание
- 2. ОСНОВНЫЕ ТЕМЫ ЛЕКЦИИ ОСНОВЫ ТЕОРИИ ИНФОРМАЦИИ ФОРМЫ ПРЕДСТАВЛЕНИЯ ДЕТЕРМИ-НИРОВАННЫХ СИГНАЛОВ СПЕКТРАЛЬНЫЙ АНАЛИЗ ПЕРИОДИЧЕС-КИХ СИГНАЛОВ ГАРМОНИЧЕСКИЙ АНАЛИЗ
- 3. ОСНОВЫ ТЕОРИИ ИНФОРМАЦИИ ИНФОРМАЦИОННЫЕ СИСТЕМЫ предна-значенны для передачи, преобразования и хранения информации. К этой группе можно
- 4. Под ИНФОРМАЦИЕЙ понимают «совокупность сведений о каких-либо событиях, процессах, объектах управления и т.п., рассматриваемых в аспекте
- 5. При всех различиях в трактовке понятия ИНФОРМАЦИЯ, бесспорно то, что проявляется информация всегда в материально-энергетической форме
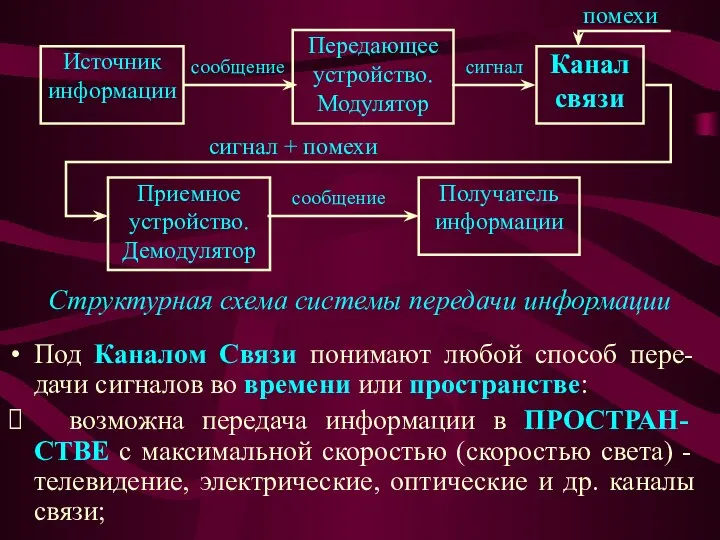
- 6. Под Каналом Связи понимают любой способ пере-дачи сигналов во времени или пространстве: ⮚ возможна передача информации
- 7. ⮚ возможна передача информации только во ВРЕМЕНИ - запись и воспроизведение инфор-мации на магнитные или оптические
- 8. Электрические сигналы принято подразделять на: детерминированные и случайные. ДЕТЕРМИНИРОВАННЫМИ называют сигналы, параметры которых точно определены в
- 9. ПОЛЕЗНЫЕ СИГНАЛЫ являются принципиально случайными колебаниями, т.к. источник сообщений выдает каждое сообщение с некоторой вероятностью и
- 10. Тем не менее, детерминированные сигналы необходимо изучать, т.к. результаты анализа детерминированных сигналов являются основой для изучения
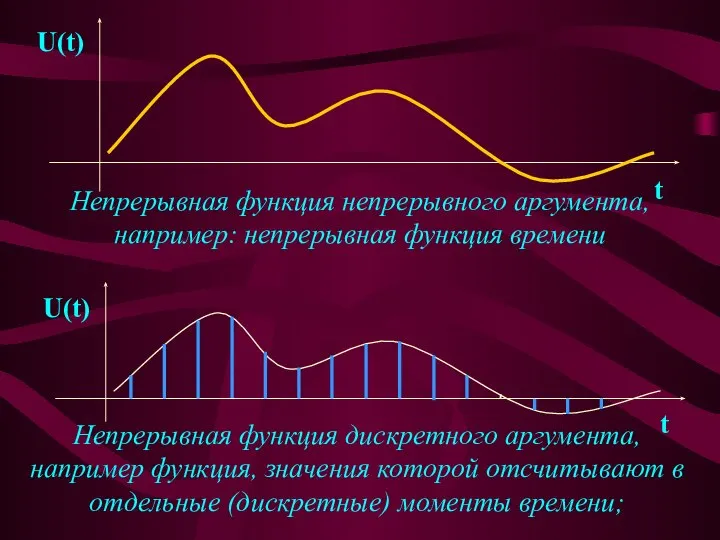
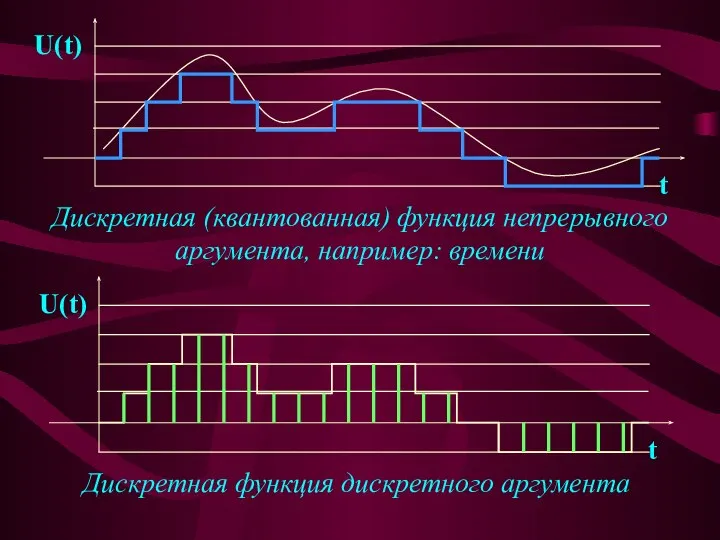
- 11. ФОРМЫ ПРЕДСТАВЛЕНИЯ ДЕТЕРМИНИРОВАННЫХ СИГНАЛОВ В зависимости от структуры информационных параметров сигналы подразделяются на: дискретные, непрерывные и
- 12. U(t) t Непрерывная функция непрерывного аргумента, например: непрерывная функция времени U(t) t Непрерывная функция дискретного аргумента,
- 14. СПЕКТРАЛЬНЫЙ АНАЛИЗ ПЕРИОДИЧЕСКИХ СИГНАЛОВ Рассмотренные математические модели сигналов отражают изменение их параметра (уровня) во времени. На
- 15. Таким образом, одни и те же сигналы можно наблюдать во временном или спектральном (частотном) базисе. Это
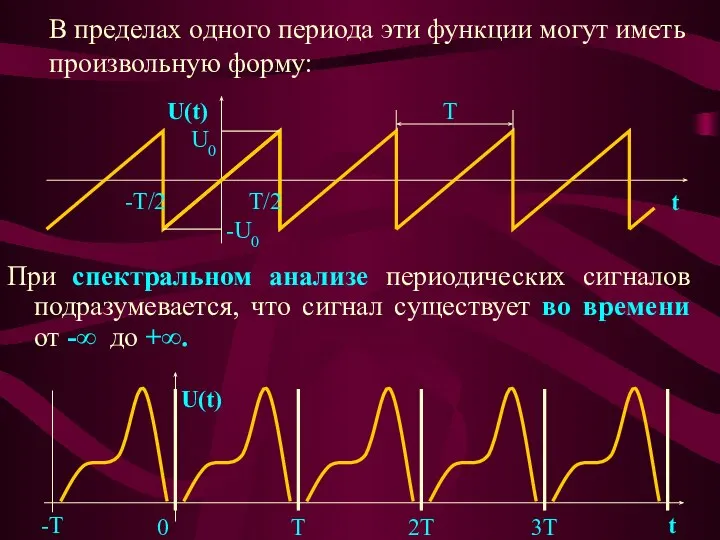
- 16. Периодическим сигналом будем называть сигнал, для которого справедливо равенство: , (1.1) где: n - целые числа
- 17. В пределах одного периода эти функции могут иметь произвольную форму: При спектральном анализе периодических сигналов подразумевается,
- 18. Временную периодическую функцию U(t) можно представить в виде дискретного спектра: , (1.2) где: (1.3) В этих
- 19. Преобразование (1.3) называют ПРЯМЫМ ПРЕОБРАЗОВАНИЕМ ФУРЬЕ для периодических сигналов. Формула (1.2) - ОБРАТНОЕ ПРЕОБРАЗОВАНИЕ ФУРЬЕ. Функцию
- 20. КОМПЛЕКСНЫЕ ЧИСЛА (в отличие от обычных, действительных) имеют два пара-метра. Эти числа можно представить в показательной
- 21. Комплексные числа можно представить двумя параметрами и в алгебраической форме : , (1.6) где: , (1.7)
- 22. Если временное представление сигнала U(t) является четной функцией времени, то синус-преобразование Фурье равно нулю: B(kω0)=0. Если
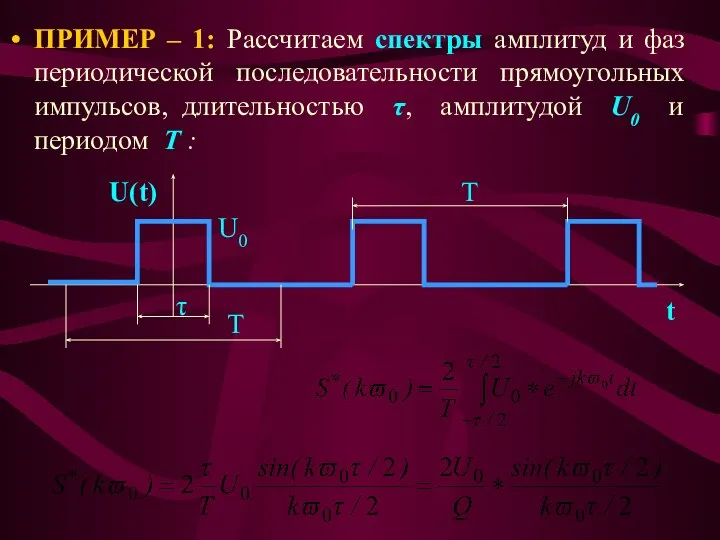
- 23. ПРИМЕР – 1: Рассчитаем спектры амплитуд и фаз периодической последовательности прямоугольных импульсов, длительностью τ, амплитудой U0
- 24. Q = T / τ - скважность импульсов. Огибающая спектра амплитуд (пунктирная линия на рис.) изменяется
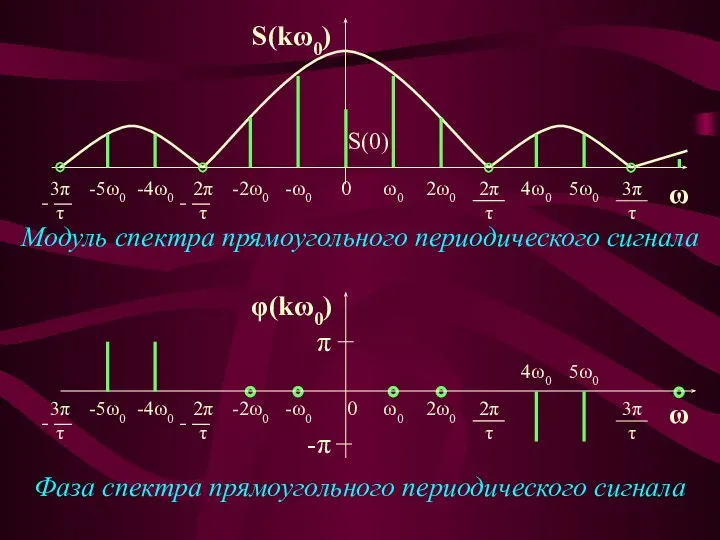
- 25. S(0) S(kω0) 4ω0 5ω0 π -π φ(kω0) Модуль спектра прямоугольного периодического сигнала Фаза спектра прямоугольного периодического
- 26. Составляющие спектра до первого нуля огибающей имеют фазы, равные нулю. После каждого перехода огибающей спектра амплитуд
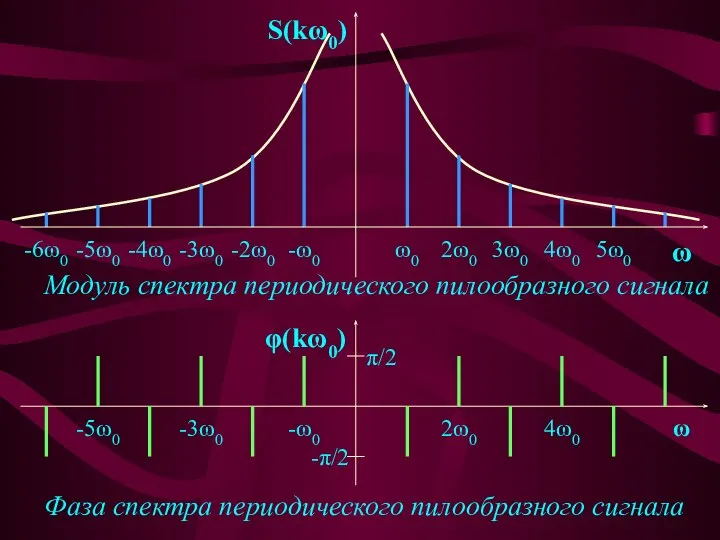
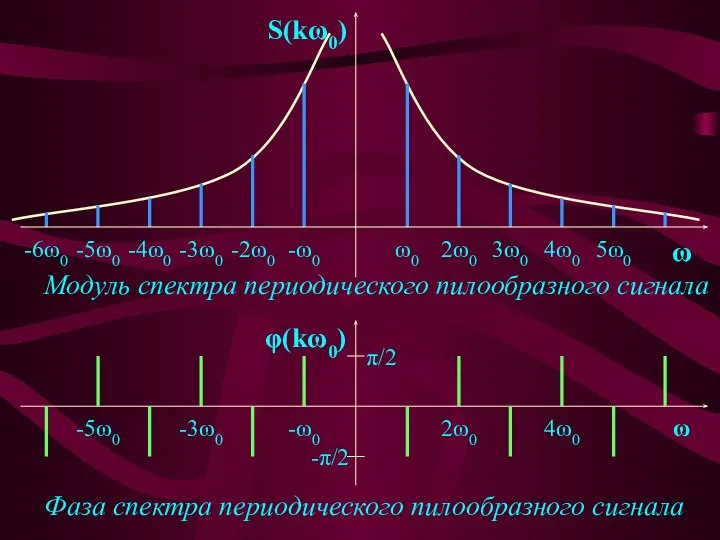
- 27. Для пилообразного сигнала, заданного временной функцией в пределах одного периода: , при : -T/2 комплексный дискретный
- 28. S(kω0) ω0 2ω0 3ω0 4ω0 5ω0 ω -ω0 -2ω0 -3ω0 -4ω0 -5ω0 -6ω0 Модуль спектра периодического
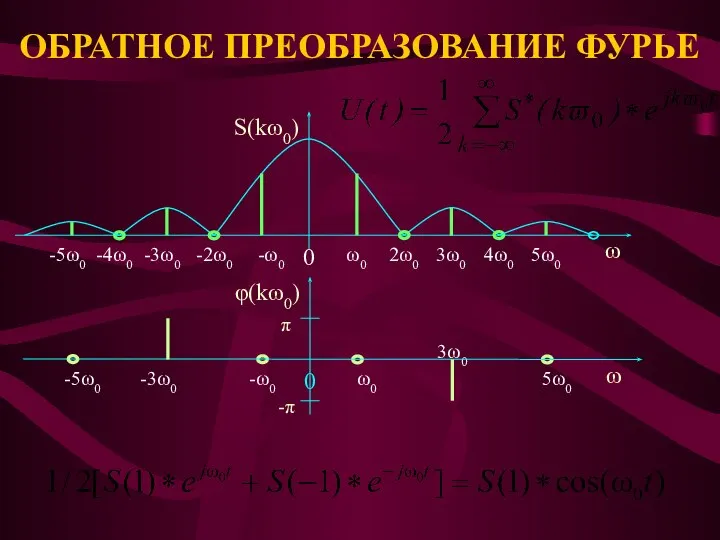
- 29. ОБРАТНОЕ ПРЕОБРАЗОВАНИЕ ФУРЬЕ
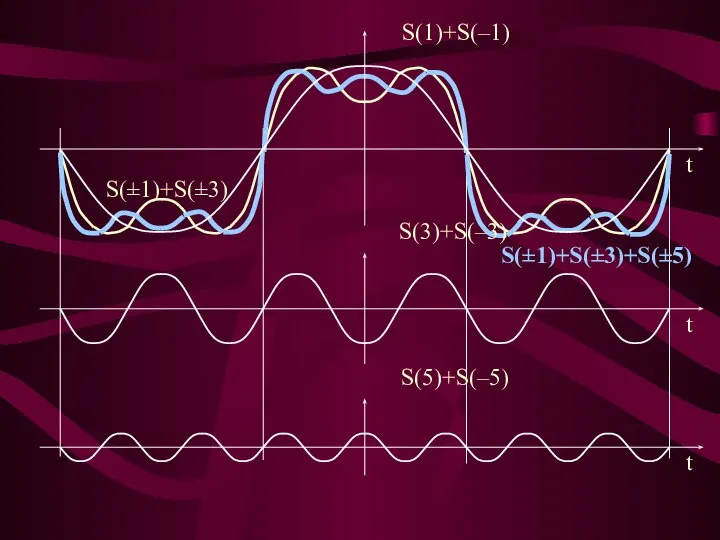
- 30. S(±1)+S(±3) S(±1)+S(±3)+S(±5)
- 31. S(kω0) ω0 2ω0 3ω0 4ω0 5ω0 ω -ω0 -2ω0 -3ω0 -4ω0 -5ω0 -6ω0 Модуль спектра периодического
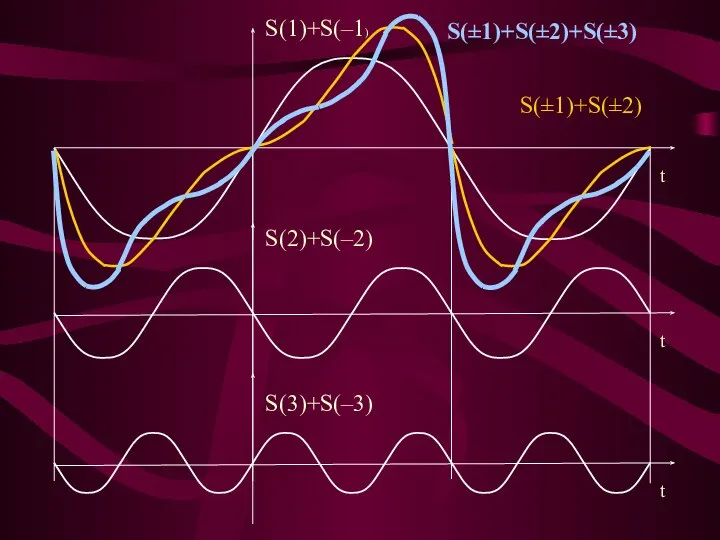
- 32. S(±1)+S(±2) S(±1)+S(±2)+S(±3)
- 33. ГАРМОНИЧЕСКИЙ АНАЛИЗ НЕПЕРИОДИЧЕСКИХ СИГНАЛОВ Реальные сигналы конечны во времени, и поэтому не могут считаться периодичес-кими. Даже
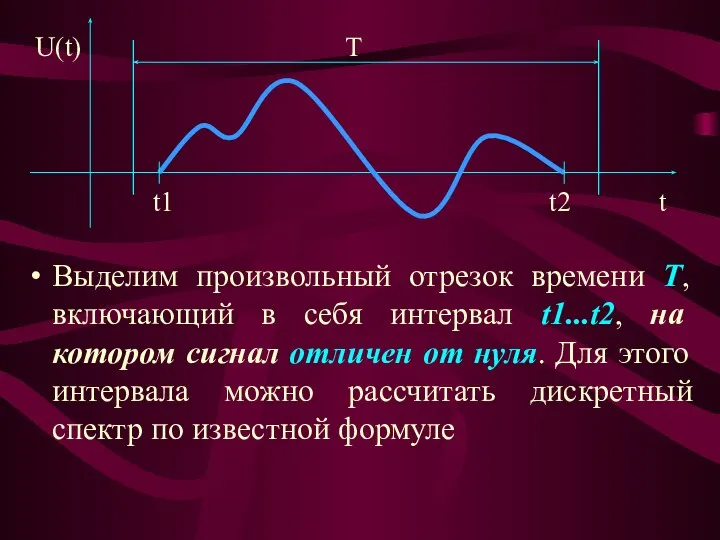
- 34. Выделим произвольный отрезок времени T, включающий в себя интервал t1...t2, на котором сигнал отличен от нуля.
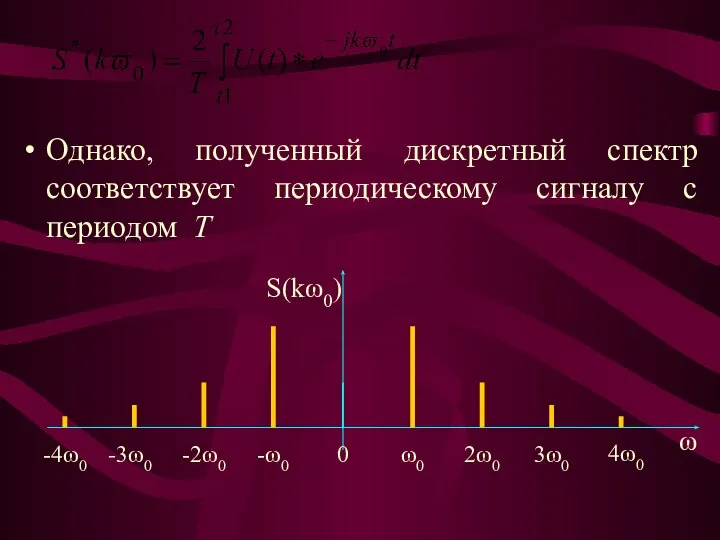
- 35. Однако, полученный дискретный спектр соответствует периодическому сигналу с периодом T S(kω0) ω0 2ω0 3ω0 -ω0 -2ω0
- 36. Для того, чтобы выбранная модель сигнала соответствовала реальному непериодическому сигналу, необходимо увеличить T от -∞ до
- 37. Поскольку спектральные составляющие S*(kω0) и расстояние между ними dω0 = 2π/T превращаются в бесконечно малые, и
- 38. Аналогично, как и с периодическими сигналами, ОБРАТНОЕ ПРЕОБРАЗОВА-НИЕ ФУРЬЕ для непериодических сигналов имеет вид: Аналогично с
- 39. где: Справедливы также формулы перехода от алгебраической формы представления комплексных чисел – в показательную:
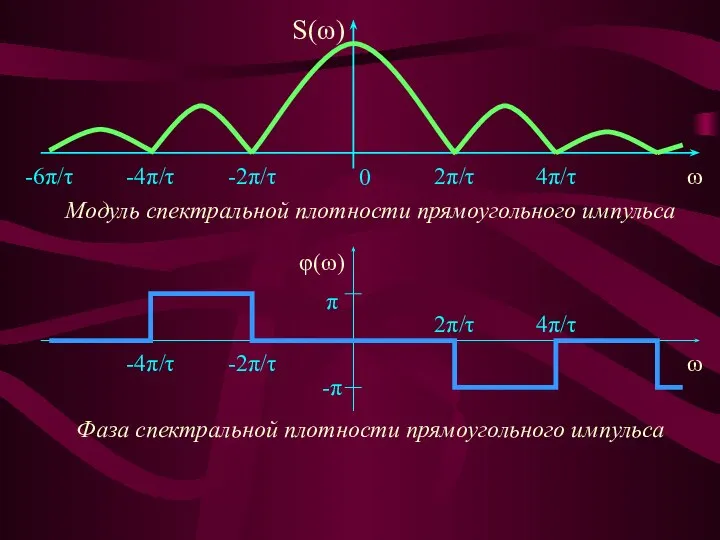
- 40. Задача 1.3 – Определим спектральную плотность одиночного прямоугольного импульса График модуля спектральной плотности одиноч-ного прямоугольного импульса
- 41. S(ω) ω 0 2π/τ 4π/τ -4π/τ -2π/τ -6π/τ Модуль спектральной плотности прямоугольного импульса ω 4π/τ 2π/τ
- 42. Отметим интересную особенность прямого и обратного ПРЕОБРАЗОВАНИЯ ФУРЬЕ. Их формулы отличаются постоянным множителем и знаком фазы.
- 43. ⮚ т.к. преобразования Лапласа и Фурье являются линейными, то алгебраической сумме исходных функций соответствует алгебраическая сумма
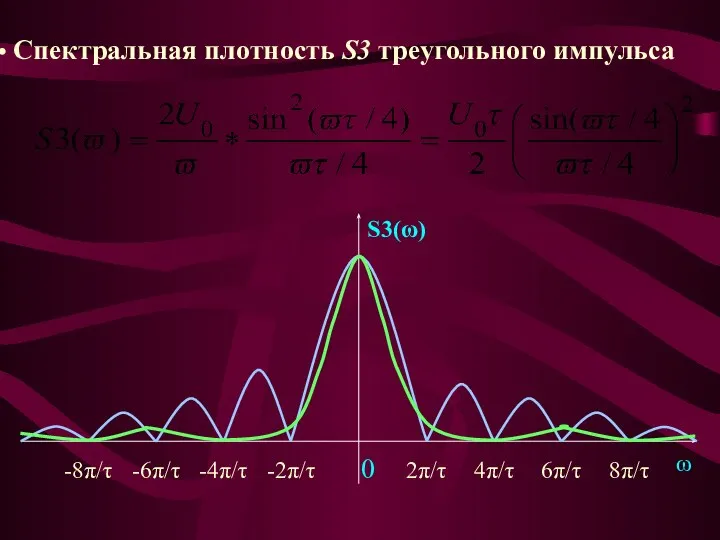
- 44. Применим эти соотношения для расчета спектральной характеристики треугольного импульса Спектральная характеристика для положительного импульса: U0 U(t)
- 45. Для отрицательного импульса спектральная харак-теристика имеет вид: Суммарная спектральная характеристика двух импульсов:
- 46. S3(ω) ω 2π/τ 4π/τ 6π/τ 8π/τ -2π/τ -4π/τ -6π/τ -8π/τ 0 Спектральная плотность S3 треугольного импульса
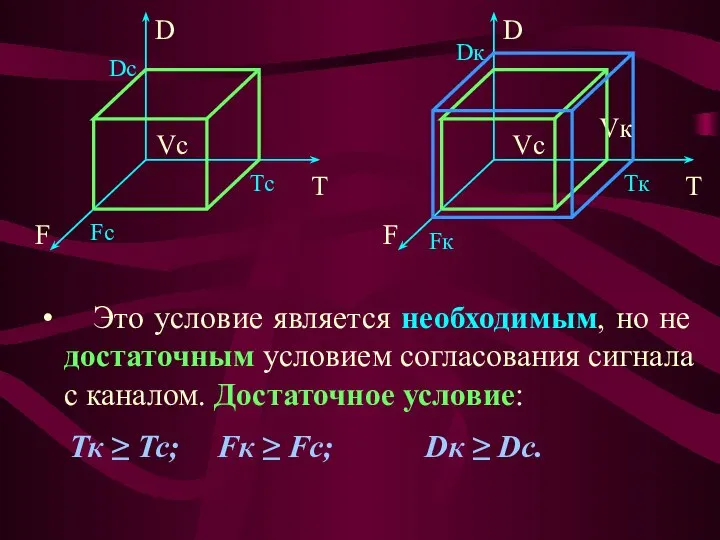
- 47. СОГЛАСОВАНИЕ СИГНАЛОВ И КАНАЛОВ СВЯЗИ Для неискаженной передачи сигнала необходимо согласование характеристик канала связи и параметров
- 48. Это условие является необходимым, но не достаточным условием согласования сигнала с каналом. Достаточное условие: Тк ≥
- 49. Если одно из этих условий не выполняется, но выполняется основное условие (Vк ≥ Vc), возможна передача
- 50. Вопросы для экспресс-контроля 1. Чем отличаются детерминированные сигналы от случайных? 2. Чем отличаются спектры периодических сиг-налов
- 51. Вопросы для экспресс-контроля 5. Назовите основные соотношения между временными функциями сигналов и их отобра-жением в спектральном
- 53. Скачать презентацию


































 Faberlic - Edelstar - Infinum faberlicrussia.com. - презентация_
Faberlic - Edelstar - Infinum faberlicrussia.com. - презентация_ Определение синуса, косинуса, тангенса и котангенса
Определение синуса, косинуса, тангенса и котангенса Органы общей компетенции в сфере экологического управления Работу выполнили Пустовая Анастасия, Мятлик Елена, группа Ю103
Органы общей компетенции в сфере экологического управления Работу выполнили Пустовая Анастасия, Мятлик Елена, группа Ю103 Презентация на тему "Образовательные программы" - скачать презентации по Педагогике
Презентация на тему "Образовательные программы" - скачать презентации по Педагогике Механізоване зварювання, наплавлення
Механізоване зварювання, наплавлення Презентация Государственные внебюджетные фонды. Задачи, признаки, функции
Презентация Государственные внебюджетные фонды. Задачи, признаки, функции Учет материально-производственных запасов
Учет материально-производственных запасов  ДИСТОЦИЯ ПЛЕЧИКОВ ПЛОДА
ДИСТОЦИЯ ПЛЕЧИКОВ ПЛОДА Презентация____
Презентация____ Программирование на языке Паскаль
Программирование на языке Паскаль Проектирование и реализация методики развития прыгучести у школьников девятых кдассов на основе динамического метода
Проектирование и реализация методики развития прыгучести у школьников девятых кдассов на основе динамического метода Стратегічний план на 2020-2022 роки
Стратегічний план на 2020-2022 роки Виртуальные базовые классы
Виртуальные базовые классы Профессиональный контакт-центр «Инфотелл» ваш надёжный партнёр в мире современных коммуникаций
Профессиональный контакт-центр «Инфотелл» ваш надёжный партнёр в мире современных коммуникаций Презентация____
Презентация____ Основные средства оптимизация товарного ассортимента в международной деятельности фирмы Юрлова В. Нечаева А.
Основные средства оптимизация товарного ассортимента в международной деятельности фирмы Юрлова В. Нечаева А.  ФОРМИ БЕЗПОСЕРЕДНЬОЇ ДЕМОКРАТІЇ В УКРАЇНІ
ФОРМИ БЕЗПОСЕРЕДНЬОЇ ДЕМОКРАТІЇ В УКРАЇНІ Основные модели организации местного самоуправления
Основные модели организации местного самоуправления МЕДИЦИНСКАЯ ЭТИКА, ОТВЕТСТВЕННОСТЬ И ПРАВА ВРАЧА Школа качества и управления Отдел маркетинга и инноваций Занятие 16
МЕДИЦИНСКАЯ ЭТИКА, ОТВЕТСТВЕННОСТЬ И ПРАВА ВРАЧА Школа качества и управления Отдел маркетинга и инноваций Занятие 16  Стретчинг Фитнес-студия "Body Balance"
Стретчинг Фитнес-студия "Body Balance" Презентация Удостоверение брачного договора
Презентация Удостоверение брачного договора №1.Какие права принадлежат собственнику? 1) владение; 2) пользование; 3) распоряжение; 4) все перечисленные права;
№1.Какие права принадлежат собственнику? 1) владение; 2) пользование; 3) распоряжение; 4) все перечисленные права;  Java 4 WEB
Java 4 WEB Параметры и характеристики приемных устройств
Параметры и характеристики приемных устройств Своя игра. Я горжусь Россией. 1 тур
Своя игра. Я горжусь Россией. 1 тур My idol. Margarita Mamun
My idol. Margarita Mamun Сестринская помощь при стенокардии1
Сестринская помощь при стенокардии1 Методика обучения броску «блейд» фрисби школьников 12-14 лет
Методика обучения броску «блейд» фрисби школьников 12-14 лет