Содержание
- 2. Плоский изгиб Расчет на прочность
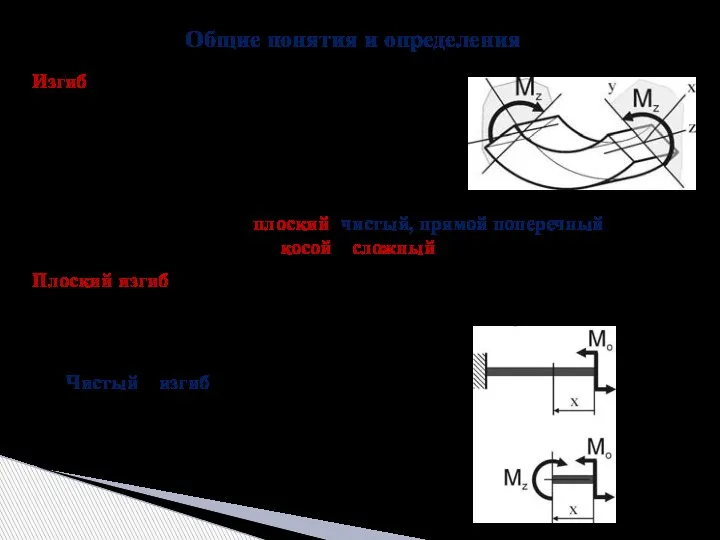
- 3. Общие понятия и определения Изгиб – деформация, при которой под действием внешних сил ось стержня изменяет
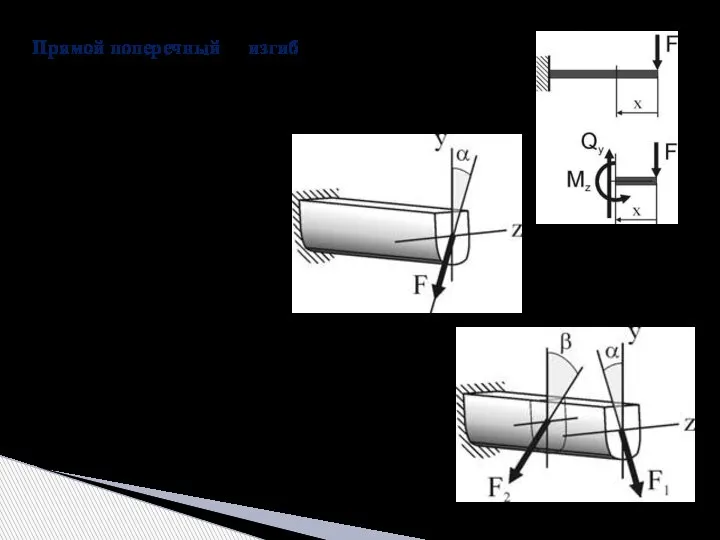
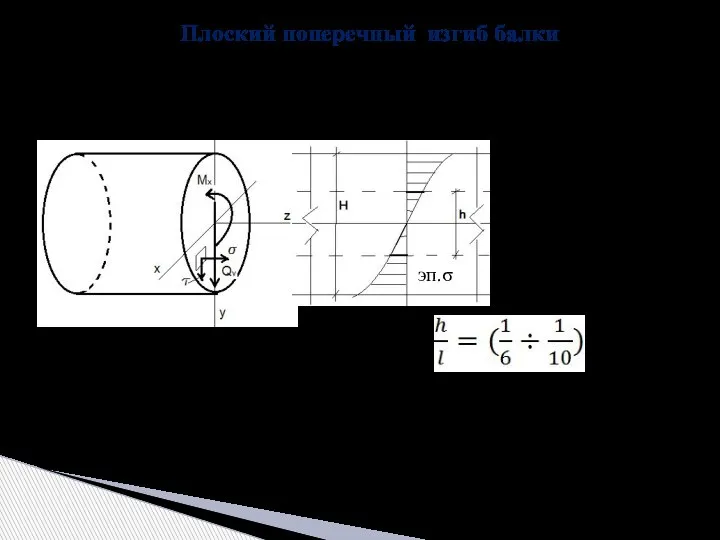
- 4. Прямой поперечный изгиб – в сечениях стержня возникают два внутренних усилия – изгибающий момент и поперечная
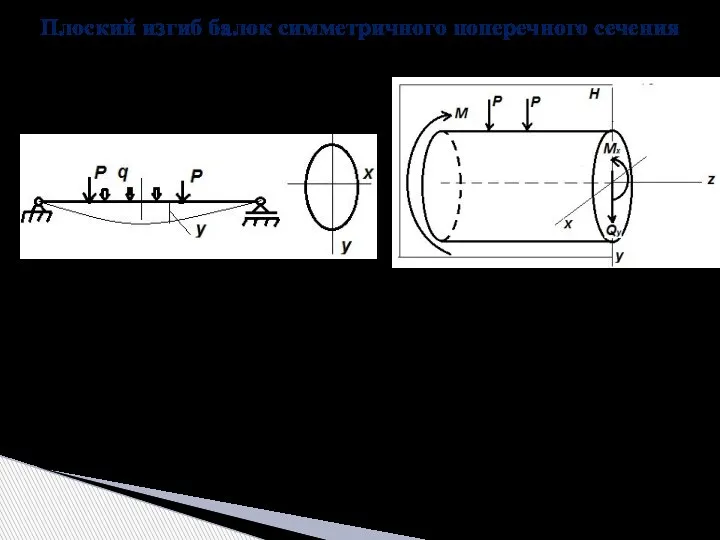
- 5. Плоский изгиб балок симметричного поперечного сечения 1) Поперечное сечение балки должно иметь хотя бы одну ось
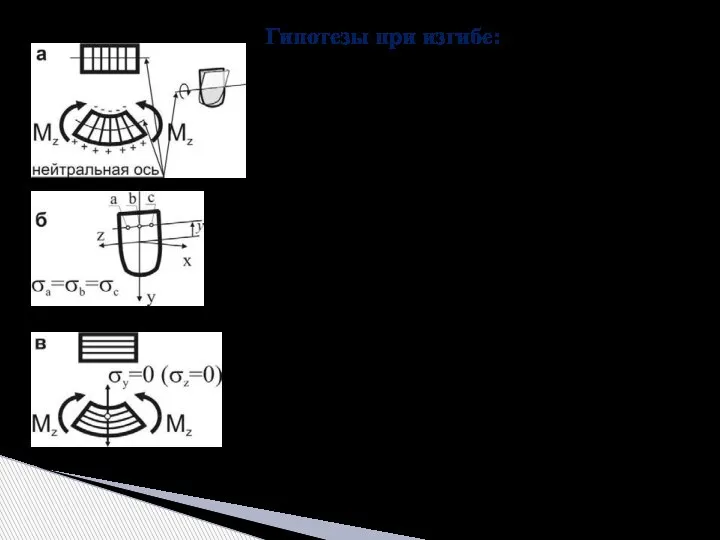
- 6. Гипотезы при изгибе: – гипотеза плоских сечений (гипотеза Бернулли) – сечения плоские до деформации остаются плоскими
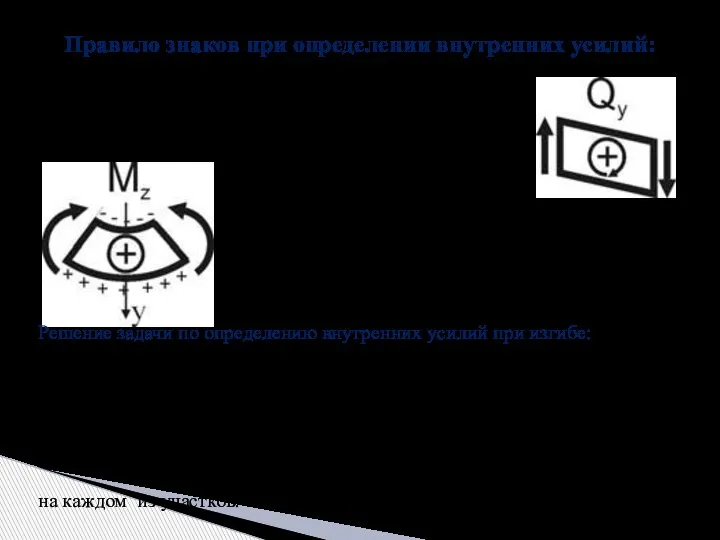
- 7. 1) поперечная сила Qy считается положительной, если она стремится повернуть рассматриваемый элемент балки по часовой стрелке;
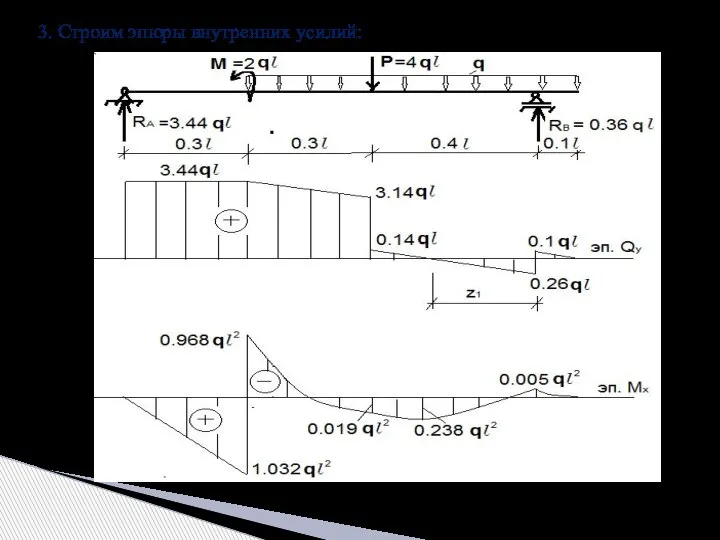
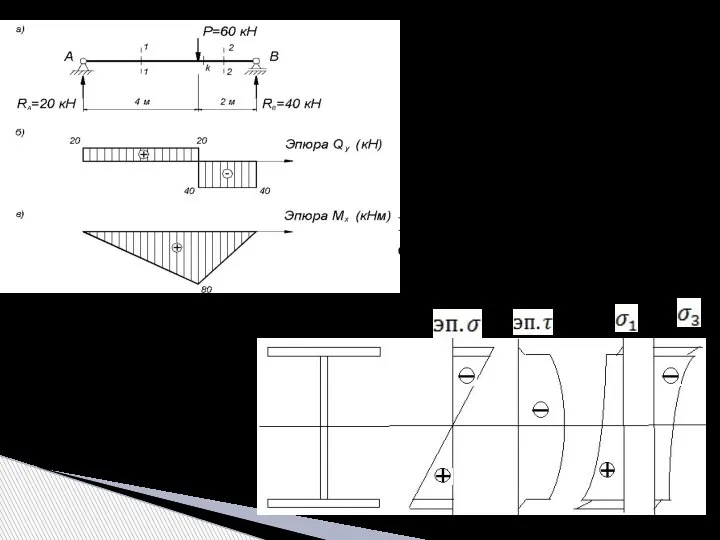
- 8. Пример построения эпюры внутренних усилий - поперечных сил и изгибающих моментов 1. Определяем опорные реакции:
- 9. 1-й участок: 0 ≤ z ≤ 0,3l При z=0, Mx=0, z=0.3 Mx=1.032ql 2. Определяем внутренние усилия:
- 10. 3-й участок: 0 ≤ z ≤ 0,4l Положение точки перехода эпюры Qy через ноль (особая точка)
- 11. 3. Строим эпюры внутренних усилий:
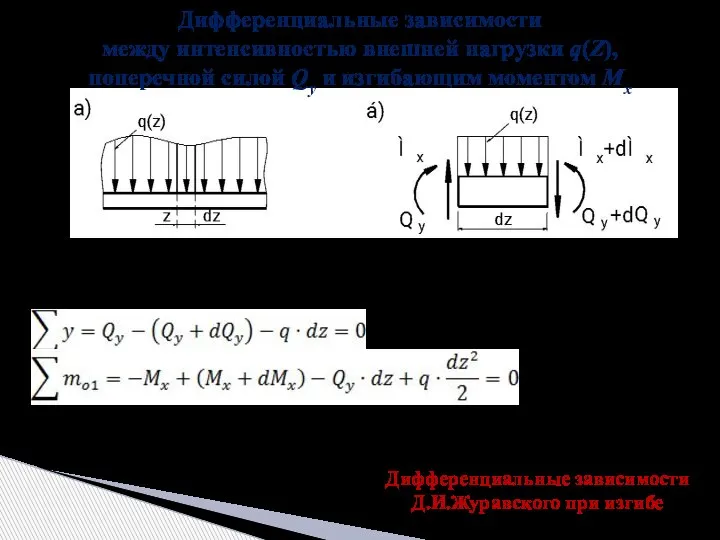
- 12. Дифференциальные зависимости между интенсивностью внешней нагрузки q(Z), поперечной силой Qy и изгибающим моментом Мx Из условия
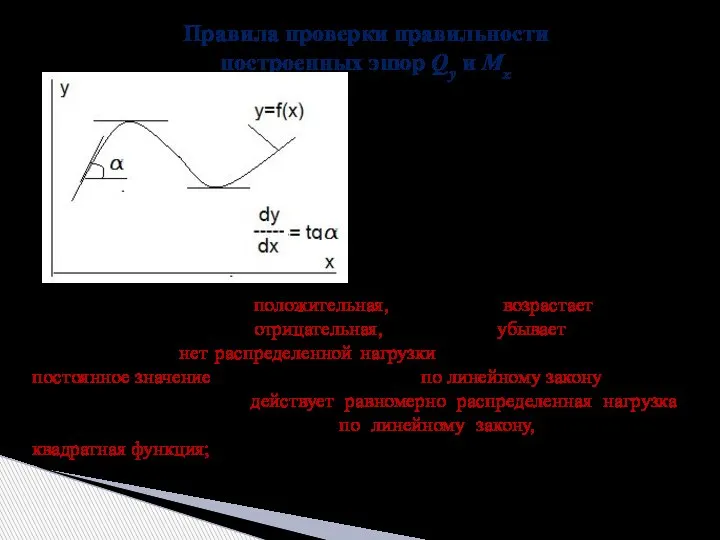
- 13. Правила проверки правильности построенных эпюр Qy и Мx Так как первая производная от функции есть тангенс
- 14. если на участке эпюра Qy переходит через нуль, то эпюра Мx в этом сечении имеет экстремальное
- 15. на защемленном конце балки эпюра Qy равна величине опорной реакции, а эпюра Mx опорному моменту; на
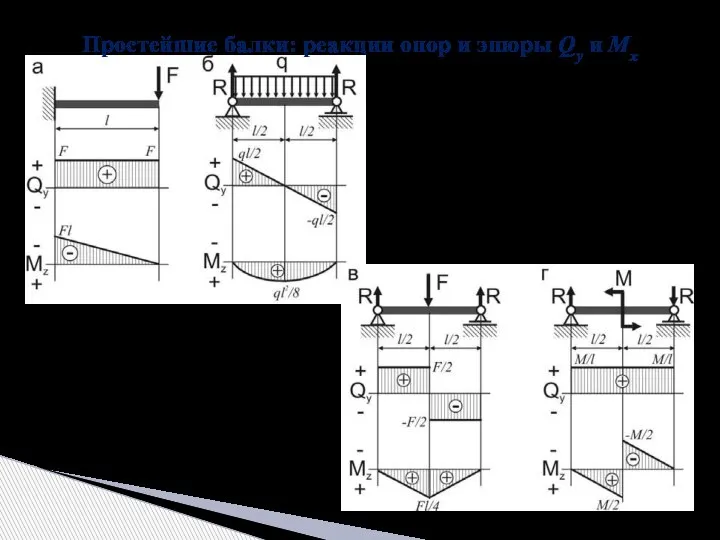
- 16. Простейшие балки: реакции опор и эпюры Qy и Мx
- 17. Определение нормальных напряжений в балке при чистом изгибе Если в пределах рассматриваемого участка балки действуют только
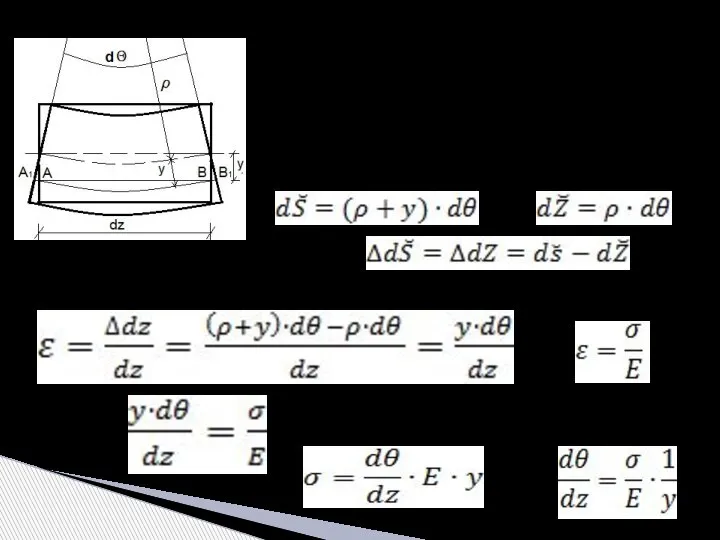
- 18. Для получения функции распределения нормальных напряжений по поперечному сечению балки рассмотрим деформированную схему бесконечно малого элемента
- 19. Поставляя значение напряжения в уравнениях равновесия получаем: отсюда видно, что статической момент инерции относительно оси х
- 20. Из формулы видно, что нормальные напряжения по высоте сечения балки меняются линейно и наибольших значений достигают
- 21. . 1.Проверочный расчет: Условие прочности балки с сечением с двумя осями симметрии: Типовые задачи: 2.Проектировочный (конструкционный)
- 22. При плоском изгибе балки, в общем случае, в поперечном сечении балки возникают поперечные силы Qу и
- 23. . 1.Проверочный расчет: Условие прочности балки по нормальным напряжениям Типовые задачи: 2.Проектировочный (конструкционный) расчет (подбор сечения):
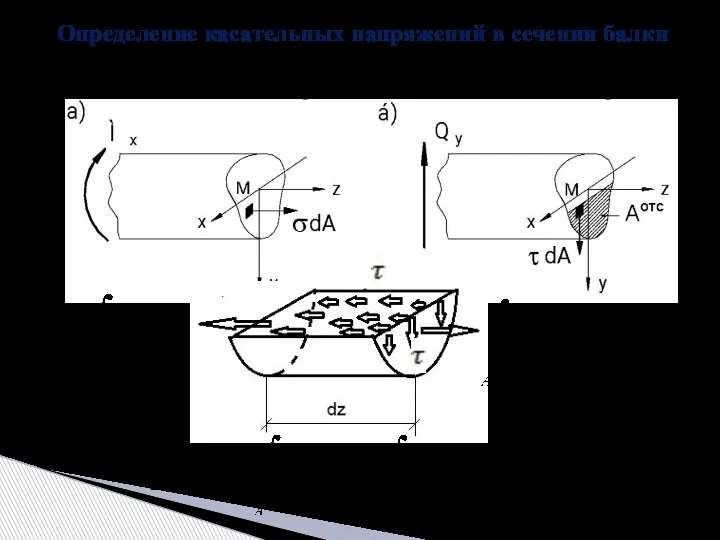
- 24. Определение касательных напряжений в сечении балки Когда в балке действуют и изгибающий момент и поперечная сила,
- 25. Отсюда получаем - формула Журавского заменяем заменяем – статический момент площади отсеченной части сечения относительно нейтральной
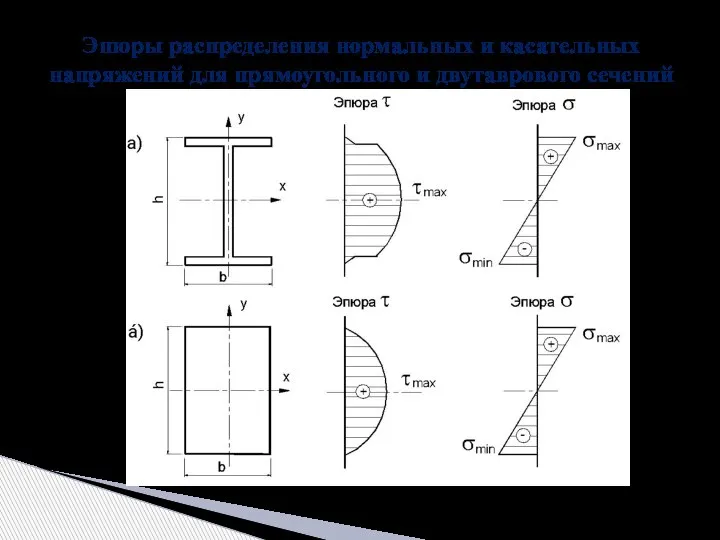
- 26. Эпюры распределения нормальных и касательных напряжений для прямоугольного и двутаврового сечений
- 27. В каждом из опасных сечений необходимо, построив эпюры напряжений, найти опасные точки (проверка прочности проводится для
- 28. При плоском поперечном изгибе балки в том сечении, где одновременно действуют большие значения изгибающего момента и
- 29. Нормальные напряжения Касательные напряжения : Главные напряжения в окрестности соответствующих точек: эп эп.
- 31. Скачать презентацию














 АБДОМИНАЛЬНАЯ БОЛЬ ПРИ СПАСТИЧЕСКИХ СОСТОЯНИЯХ ЖЕЛЧЕВЫВОДЯЩИХ ПУТЕЙ, ЖЕЛЧНОКАМЕННОЙ БОЛЕЗНИ, ПОСТХОЛЕЦИСТЭКТОМИЧЕСКОМ СИНД
АБДОМИНАЛЬНАЯ БОЛЬ ПРИ СПАСТИЧЕСКИХ СОСТОЯНИЯХ ЖЕЛЧЕВЫВОДЯЩИХ ПУТЕЙ, ЖЕЛЧНОКАМЕННОЙ БОЛЕЗНИ, ПОСТХОЛЕЦИСТЭКТОМИЧЕСКОМ СИНД Судебная практика по компьютерным преступлениям В.Г. Мисликов (группа Ю-103)
Судебная практика по компьютерным преступлениям В.Г. Мисликов (группа Ю-103) Жан Ануй (Jean Anouilh) (1910-1987)
Жан Ануй (Jean Anouilh) (1910-1987) Тема 2-2
Тема 2-2 Подвиг героя. Перов Александр Валентинович
Подвиг героя. Перов Александр Валентинович Cознание и деятельность Развитие психики в филогенезе. Гипотезы о происхождении сознания
Cознание и деятельность Развитие психики в филогенезе. Гипотезы о происхождении сознания Myślimy jak Chrystus
Myślimy jak Chrystus Правила определения объемов строительных работ
Правила определения объемов строительных работ Петушок – золотой гребешок
Петушок – золотой гребешок  проект Богатства отданные людям
проект Богатства отданные людям Учитель МХК Еремина О. Ю. Интегрированный урок по МХК
Учитель МХК Еремина О. Ю. Интегрированный урок по МХК Особенности договора поставки товаров для государственных нужд
Особенности договора поставки товаров для государственных нужд Экономическая теория
Экономическая теория  Тампонажный состав для цементирования интервалов ММП (многолетне-мерзлых пород)
Тампонажный состав для цементирования интервалов ММП (многолетне-мерзлых пород) Презентация на тему "Портфоліо учнів 2-Б класу Жидачівської ЗОШ №2" - скачать презентации по Педагогике
Презентация на тему "Портфоліо учнів 2-Б класу Жидачівської ЗОШ №2" - скачать презентации по Педагогике Язык программирования С++
Язык программирования С++ Преобразователи, используемые при испытаниях автомобилей и тракторов. Типичная функциональная схема канала ИИС
Преобразователи, используемые при испытаниях автомобилей и тракторов. Типичная функциональная схема канала ИИС Даниил Журов
Даниил Журов Роботы будущего
Роботы будущего Элементы квантовой статистики
Элементы квантовой статистики  Работу выполнил ученик 4 А класса МБОУ «СОШ № 5» Дрига Никита Руководитель: Учитель начальных классов МБОУ «СОШ № 5» С
Работу выполнил ученик 4 А класса МБОУ «СОШ № 5» Дрига Никита Руководитель: Учитель начальных классов МБОУ «СОШ № 5» С Муниципальное общеобразовательное учреждение «Средняя общеобразовательная школа № 5» г. Нижняя Салда
Муниципальное общеобразовательное учреждение «Средняя общеобразовательная школа № 5» г. Нижняя Салда Тест по стилям архитектуры
Тест по стилям архитектуры Совершенствование организации технического обслуживания и ремонта техники в ООО «Кипенская СХТ» Ленинградской области
Совершенствование организации технического обслуживания и ремонта техники в ООО «Кипенская СХТ» Ленинградской области Комплексный учебный курс "Основы религиозных культур и светской этики»: цели, задачи
Комплексный учебный курс "Основы религиозных культур и светской этики»: цели, задачи Работоспособность металлопленочных конденсаторов в режимах высокой токовой нагрузки
Работоспособность металлопленочных конденсаторов в режимах высокой токовой нагрузки Пироэлектрики
Пироэлектрики Презентация на тему "Имплантация зубов любой сложности" - скачать презентации по Медицине
Презентация на тему "Имплантация зубов любой сложности" - скачать презентации по Медицине