Теперь наша задача состоит в определении числа степеней свободы, которыми обладает
электромагнитное излучение в полости вокруг абсолютно чёрного тела.
Определив число степеней свободы, мы сможем выразить энергию электромагнитного поля через температуру. Так как система находится в термодинамическом равновесии, температура тела равно температуре излучения. Основываясь на этом, мы сможем выразить излучательную способность тела, как функцию температуры. (Спектральную плотность энергии ЭМП мы уже можем выражать через излучательную способность).
Полость замкнута. Система находится в состоянии термодинамического равновесия. Следовательно, энергия ЭМП в полости постоянна и никуда не переносится электромагнитными волнами.
Очевидно, что единственной формой электромагнитной волны, которая не переносит энергию является стоячая волна. Следовательно, ЭМП в полости может существовать только в виде стоячих электромагнитных волн.
Будем считать, что с каждой стоячей электромагнитной волной связаны две степени свободы: одна – с колебаниями напряжённости электрического поля, вторая – с колебаниями напряжённости магнитного поля.
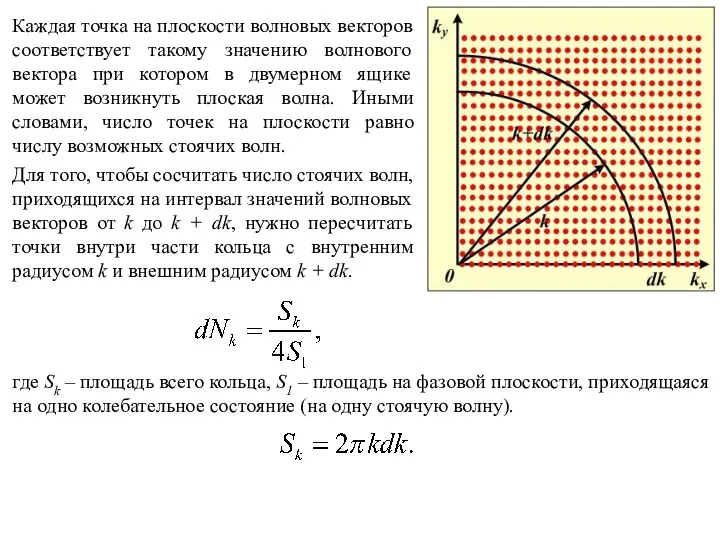
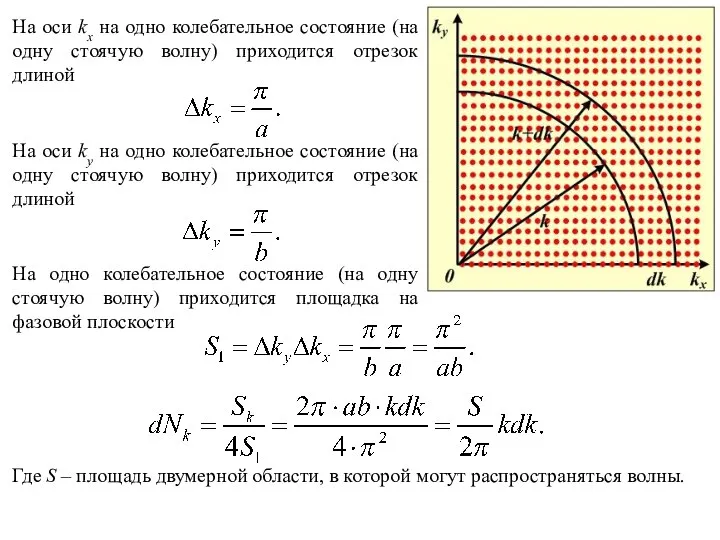
Чтобы найти число степеней свободы электромагнитного поля в полости, нужно найти число стоячих волн, возникающих в этой полости и умножить его на два.















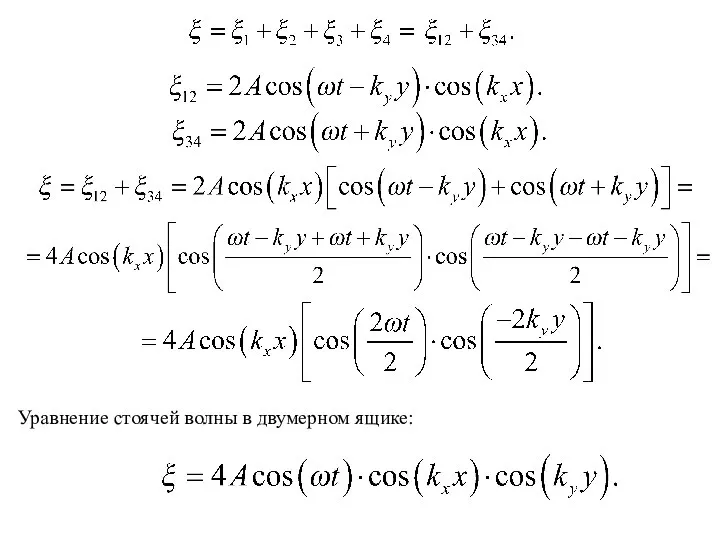

 Презентация МЕЖДУНАРОДНОЕ ПРАВО Источники международного права
Презентация МЕЖДУНАРОДНОЕ ПРАВО Источники международного права  судебный контроль за законностью осуществления исполнительной власти Выполнила: студентка 2 курса группы Э091 экономического факу
судебный контроль за законностью осуществления исполнительной власти Выполнила: студентка 2 курса группы Э091 экономического факу Логические основы ЭВМ
Логические основы ЭВМ Отогенные и риногенные внутричерепные осложнения
Отогенные и риногенные внутричерепные осложнения «Величины. Единица длины – километр». Болвина Ирина Владимировна Учитель начальных классов Боровская СОШ №1 Тюменского района
«Величины. Единица длины – километр». Болвина Ирина Владимировна Учитель начальных классов Боровская СОШ №1 Тюменского района Основные вехи жизни и деятельности свт. Филарета, характеристика личности, богословское наследие, особенности стиля
Основные вехи жизни и деятельности свт. Филарета, характеристика личности, богословское наследие, особенности стиля КпоС
КпоС Цены и особенности ценообразования на мировых рынках Юрлова Виктория, М-102
Цены и особенности ценообразования на мировых рынках Юрлова Виктория, М-102  Презентация на тему "Личностно-ориентированный и индивидуальный подход в обучении учащихся" - скачать презентации по Педагог
Презентация на тему "Личностно-ориентированный и индивидуальный подход в обучении учащихся" - скачать презентации по Педагог Презентация "Малотоннажные установки производства моторных топлив" - скачать презентации по Экономике
Презентация "Малотоннажные установки производства моторных топлив" - скачать презентации по Экономике Детали приборов и основы конструирования
Детали приборов и основы конструирования К.А.Григорьева кафедра зарубежной литературы и журналистики Саратовский госуниверситет Американский Уголок в Саратове К
К.А.Григорьева кафедра зарубежной литературы и журналистики Саратовский госуниверситет Американский Уголок в Саратове К ФГОС в ДОУ Образовательная область «Художественно-эстетическое развитие» раздел «Музыка» Музыкальный руководитель: Кухта О
ФГОС в ДОУ Образовательная область «Художественно-эстетическое развитие» раздел «Музыка» Музыкальный руководитель: Кухта О Латинский язык. Занятие 5
Латинский язык. Занятие 5 Военно-спортивная игра "Зарница". Команда МБОУ «Школа №167»
Военно-спортивная игра "Зарница". Команда МБОУ «Школа №167» Начертательная геометрия и инженерная графика. Развертки. Лекция 14
Начертательная геометрия и инженерная графика. Развертки. Лекция 14 Музыка (элитарная) Подготовили: студентки II курса Группы Э-101 Жолобова Юлия Сахарова Мария Комарова Мария
Музыка (элитарная) Подготовили: студентки II курса Группы Э-101 Жолобова Юлия Сахарова Мария Комарова Мария Революция и эволюция
Революция и эволюция Органы, осуществляющие предварительное следствие Выполнила Тарасенко Александра, студент группы Ю101
Органы, осуществляющие предварительное следствие Выполнила Тарасенко Александра, студент группы Ю101 Муфта, Полботинка и Моховая Борода - ч.2 - презентация для начальной школы
Муфта, Полботинка и Моховая Борода - ч.2 - презентация для начальной школы Управление процессом становления и развития нового качества образования
Управление процессом становления и развития нового качества образования Презентация на тему "Константин Дмитриевич Ушинский" - скачать презентации по Педагогике
Презентация на тему "Константин Дмитриевич Ушинский" - скачать презентации по Педагогике Сервис Ориентированная Архитектура Java Web Services
Сервис Ориентированная Архитектура Java Web Services Каталитическая печь медленного горения и система приготовления горячей воды
Каталитическая печь медленного горения и система приготовления горячей воды Презентация_modif
Презентация_modif  «ПОМНИ ПРАВИЛА ДВИЖЕНЬЯ КАК ТАБЛИЦУ УМНОЖЕНЬЯ»
«ПОМНИ ПРАВИЛА ДВИЖЕНЬЯ КАК ТАБЛИЦУ УМНОЖЕНЬЯ»  Социальная политика государства. (Тема 15)
Социальная политика государства. (Тема 15) Презентация_____
Презентация_____