Содержание
- 2. Логическое продолжение понятия двойного интеграла, когда областью интегрирования является некоторая поверхность, а подынтегральной функцией служит функция
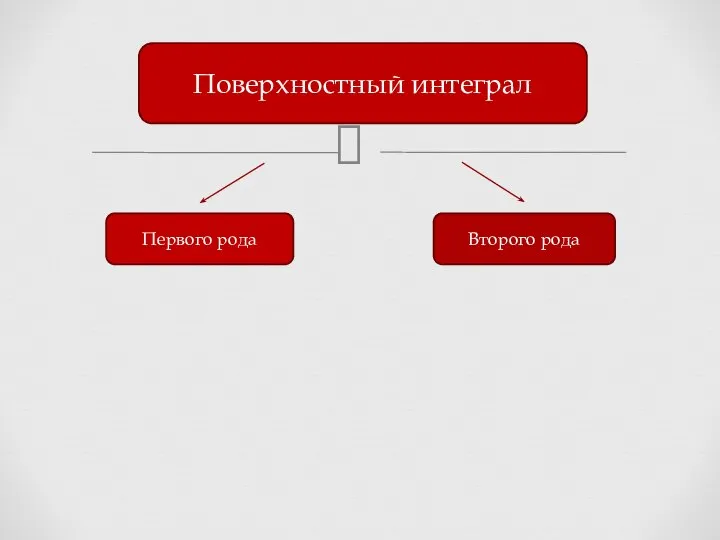
- 3. Поверхностный интеграл Первого рода Второго рода
- 4. Разобьём поверхность σ на n непересекающихся элементарных поверхностей, найдём элемент массы i -го элемента разбиения Δmi=
- 5. если он существует, не зависит от способа разбиения поверхности σ на элементарные поверхности и выбора точек
- 6. Интегральной суммой 1-го рода для функции f(x, y, z) поверхности называется сумма произведений значений функции в
- 7. Чтобы вычислить поверхностный интеграл по площади, нужно привести его к двойному интегралу: в подынтегральную функцию вместо
- 8. Постоянный множитель можно выносить за знак поверхностного интеграла первого рода Поверхностный интеграл первого рода алгебраической суммы
- 9. Свойства
- 10. Теорема о среднем для поверхностного интеграла первого рода
- 11. Приложения поверхностного интеграла Пусть Ф −материальная поверхность с поверхностной плотностью ρ(x, y, z) в точке M(x,
- 14. Скачать презентацию










 Собрание и комитет кредиторов. Право на информацию. (Лекция 3)
Собрание и комитет кредиторов. Право на информацию. (Лекция 3) Недоношенные дети
Недоношенные дети  Электронды парамагнитті резонанс әдісі (ЭПР)
Электронды парамагнитті резонанс әдісі (ЭПР) Программирование на Паскале – первый уровень
Программирование на Паскале – первый уровень Право на свободу слова
Право на свободу слова Вязание узлов в альпинизме
Вязание узлов в альпинизме ФЗ №399 об изменениях в ФЗ 261
ФЗ №399 об изменениях в ФЗ 261 Игровые аспекты принятия решений
Игровые аспекты принятия решений Русское зодчество в XVI-XVII веках
Русское зодчество в XVI-XVII веках Turkey-EU relations after Özal
Turkey-EU relations after Özal Указатели
Указатели Буквосочетания ЧК, ЧН, ЧТ. Правило правописания сочетаний чк, чн, чт, нч. Юскина Лидия Николаевна МОУ Остроленская СОШ Нагайбак
Буквосочетания ЧК, ЧН, ЧТ. Правило правописания сочетаний чк, чн, чт, нч. Юскина Лидия Николаевна МОУ Остроленская СОШ Нагайбак Первое приложение на ASP.NET
Первое приложение на ASP.NET Аттестация испытательного оборудования
Аттестация испытательного оборудования Презентация на тему "Закаливание" - скачать презентации по Медицине
Презентация на тему "Закаливание" - скачать презентации по Медицине Презентация "Экономика России в первой четверти XVIII века" - скачать презентации по Экономике
Презентация "Экономика России в первой четверти XVIII века" - скачать презентации по Экономике Реконструкция подстанции 110/35/10 кВ «Апшеронская»
Реконструкция подстанции 110/35/10 кВ «Апшеронская» Цирк
Цирк Приветствия
Приветствия Саяси билік
Саяси билік Ценовая политика компании «Coca-Cola
Ценовая политика компании «Coca-Cola Электронные выпрямители. Классификация. Идеализация схем выпрямления
Электронные выпрямители. Классификация. Идеализация схем выпрямления Команда «Хранители». МБОУ «Больше-Кочинская СОШ». Туристический маршрут «Село Большая Коча – центр обрядовой культуры»
Команда «Хранители». МБОУ «Больше-Кочинская СОШ». Туристический маршрут «Село Большая Коча – центр обрядовой культуры» ВАСИЛИЙ СУРИКОВ «Боярыня Морозова» «Степан Разин» «Утро стрелецкой казни» «Меньшиков в Березове» «Покорение Сибири Ермако
ВАСИЛИЙ СУРИКОВ «Боярыня Морозова» «Степан Разин» «Утро стрелецкой казни» «Меньшиков в Березове» «Покорение Сибири Ермако Arduino робот своими руками
Arduino робот своими руками Продвижение персонала: формирование резерва кадров и планирование карьеры Контрольная работа по дисциплине: Управление персона
Продвижение персонала: формирование резерва кадров и планирование карьеры Контрольная работа по дисциплине: Управление персона Предложения общественного объединения «Наше Лианозово» по продлению Люблинско-Дмитровской линии Московского метрополитена
Предложения общественного объединения «Наше Лианозово» по продлению Люблинско-Дмитровской линии Московского метрополитена Информатика. Суперскалярность
Информатика. Суперскалярность