Содержание
- 2. Актуализация опорных знаний Вопросы 1) Что называется первообразной? 2) Что называется неопределённым интегралом? 3) Сформулировать свойства
- 3. Актуализация опорных знаний
- 4. Актуализация опорных знаний
- 5. Актуализация опорных знаний Вопросы: 4) Назовите действие обратное интегрированию. 5) Назовите методы интегрирования. 5) Правильность интегрирования
- 6. Содержание Задача о площади криволинейной трапеции Понятие интегральной суммы Геометрический смысл интегральной суммы Понятие определенного интеграла
- 7. Задача о площади криволинейной трапеции Пусть на отрезке [a, b] задана неотрицательная функция у=f(х). Требуется найти
- 8. Понятие интегральной суммы
- 9. Геометрический смысл интегральной суммы Sл= S1 + S2 +...+ Sn
- 10. Понятие определенного интеграла
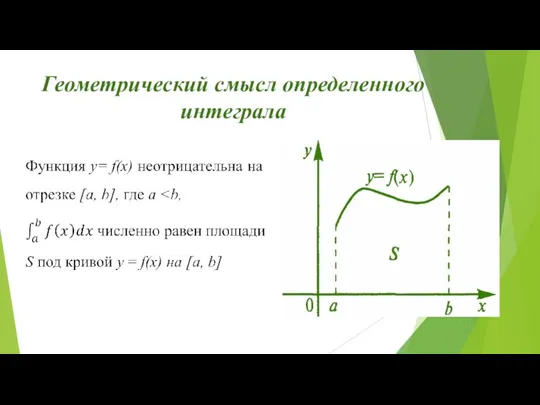
- 11. Геометрический смысл определенного интеграла
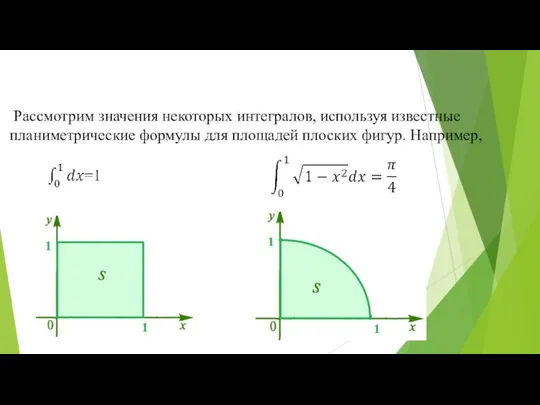
- 12. Рассмотрим значения некоторых интегралов, используя известные планиметрические формулы для площадей плоских фигур. Например,
- 13. Экономический смысл интеграла
- 14. Экономический смысл интеграла
- 15. Условие существования определенного интеграла Теорема. Если функция у =f (x) непрерывна на отрезке [а, b], то
- 16. Пример нахождения определенного интеграла на основании определения Вычислить
- 17. Известно, что сумма квадратов чисел натурального ряда равна Пример нахождения определенного интеграла на основании определения Непосредственное
- 18. Интересно отметить, что впервые задачу этого рода решил Архимед. При помощи рассуждений, которые отдаленно напоминают современный
- 19. 1. Свойства определенного интеграла Определенный интеграл с одинаковыми пределами интегрирования равен нулю Доказательство
- 20. 2. Свойства определенного интеграла При перемене местами верхнего и нижнего пределов интегрирования определенный интеграл меняет свой
- 21. 3. Свойства определенного интеграла Доказательство
- 22. 4. Свойства определенного интеграла Постоянный множитель можно выносить за знак интеграла, т.е. Доказательство
- 23. 5. Свойства определенного интеграла Интеграл от алгебраической суммы двух функций равен такой же сумме интегралов от
- 24. 6. Свойства определенного интеграла По свойству 5 получаем т.е. обе части неравенства можно почленно интегрировать. Если
- 25. 7. Свойства определенного интеграла Если отрезок интегрирования разбит на части, то интеграл на всем отрезке равен
- 26. 8. Свойства определенного интеграла Если M – наибольшее значение функции f(x) на отрезке [a;b], а m
- 27. a) Интеграл от нечетной функции по симметричному отрезку равен нулю 9. Свойства определенного интеграла b) Интеграл
- 28. 9. Свойства определенного интеграла Доказательство
- 29. Теорема. Если функция непрерывна на [а, b], то существует такая точка, что Теорема о среднем Доказательство
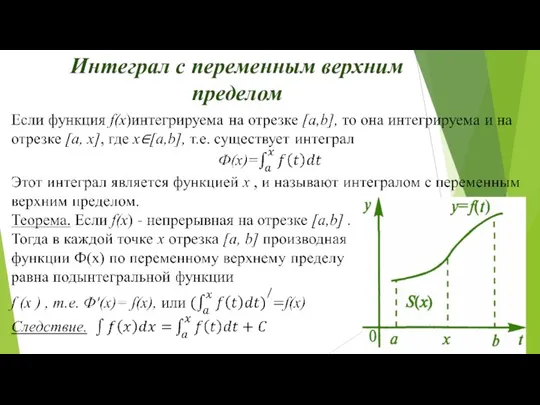
- 30. Интеграл с переменным верхним пределом
- 31. Формула Ньютона - Лейбница Теорема. Если F(x)есть некоторая первообразная от непрерывной функции f(x), то справедлива формула
- 32. Формула Ньютона - Лейбница
- 33. Пример
- 34. Пример Вычислить:
- 35. Решение
- 36. Решение Используя формулу получим
- 37. Пример Вычислить:
- 38. Решение
- 40. Скачать презентацию





![Задача о площади криволинейной трапеции Пусть на отрезке [a, b] задана](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/1306503/slide-6.jpg)



















![Теорема. Если функция непрерывна на [а, b], то существует такая точка, что Теорема о среднем Доказательство](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/1306503/slide-28.jpg)








 Межбюджетные отношения
Межбюджетные отношения «Использование индивидуальных и групповых форм работы на уроках математики с учетом личностно – ориентированного подхода к учащ
«Использование индивидуальных и групповых форм работы на уроках математики с учетом личностно – ориентированного подхода к учащ Отклонения и допуски расположения рассматриваемого элемента (ГОСТ 24642-83)
Отклонения и допуски расположения рассматриваемого элемента (ГОСТ 24642-83) Reversing the engine
Reversing the engine Технология устройства защитных покрытий
Технология устройства защитных покрытий Альпийский подвижный пояс
Альпийский подвижный пояс  Эволюция взглядов на управление
Эволюция взглядов на управление Подготовительные недели. Особенности богослужения и поведения в храме
Подготовительные недели. Особенности богослужения и поведения в храме Обработка косвенных измерений
Обработка косвенных измерений  Панас Мирний
Панас Мирний  Камалян А.К., д.э.н., профессор, зав. кафедрой налогов и права ВГАУ
Камалян А.К., д.э.н., профессор, зав. кафедрой налогов и права ВГАУ  Мікропроцесорна техніка. PSoC Creator 4.2 Designing with PSoC 3/5. (Лекція 11)
Мікропроцесорна техніка. PSoC Creator 4.2 Designing with PSoC 3/5. (Лекція 11) Разработка инновационного проекта
Разработка инновационного проекта Законодательные и исполнительные органы государственной власти субъектов Российской Федерации
Законодательные и исполнительные органы государственной власти субъектов Российской Федерации Презентация на тему "Формирование правильной осанки средствами ритмической гимнастики" - скачать презентации по Медицине
Презентация на тему "Формирование правильной осанки средствами ритмической гимнастики" - скачать презентации по Медицине Представления о культуре К.Г. Юнга
Представления о культуре К.Г. Юнга Россия на международном рынке «Халяль»: основные тенденции и возможности
Россия на международном рынке «Халяль»: основные тенденции и возможности Meine Familie. Berufe
Meine Familie. Berufe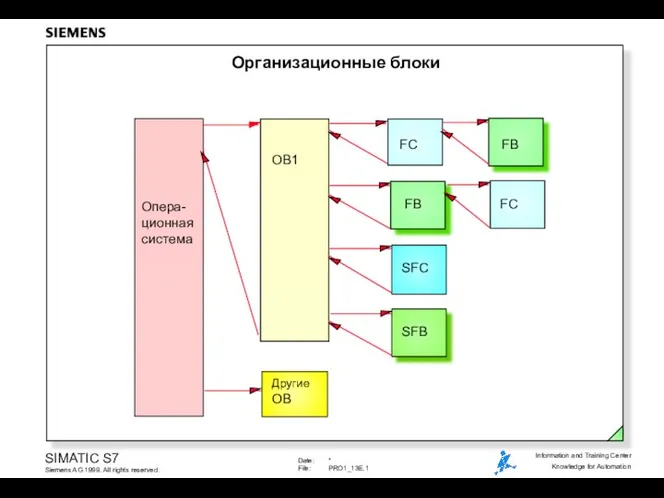 Организационные блоки
Организационные блоки Право, часть 1, вопросы кодификатора. 9 класс. Тема 6
Право, часть 1, вопросы кодификатора. 9 класс. Тема 6 Параллельное программирование. OpenMP
Параллельное программирование. OpenMP Как построить новый дом? Урок окружающего мира во 2 классе
Как построить новый дом? Урок окружающего мира во 2 классе Принципи навчання української мови
Принципи навчання української мови Досуг группы продлённого дня 1 классов.
Досуг группы продлённого дня 1 классов. Двигательная активность
Двигательная активность Стратегический менеджмент. Этапы стратегического управления
Стратегический менеджмент. Этапы стратегического управления Рост и развитие хлебных злаков
Рост и развитие хлебных злаков  Презентация урока русского языка в 3 классе по теме «Правописание гласных и согласных в корне слова»
Презентация урока русского языка в 3 классе по теме «Правописание гласных и согласных в корне слова»