Содержание
- 2. Каждой функции f(t) из пространства можно поставить в соответствие ряд Фурье. где коэффициенты Фурье определяются формулами
- 3. Когда говорят, что функция f(t) равна ряду Фурье (2) то имеют в виду, что существует следующий
- 4. Система функций Радемахера В качестве ортогональной системы функций можно взять систему функций Радемахера. Система функций Радемахера
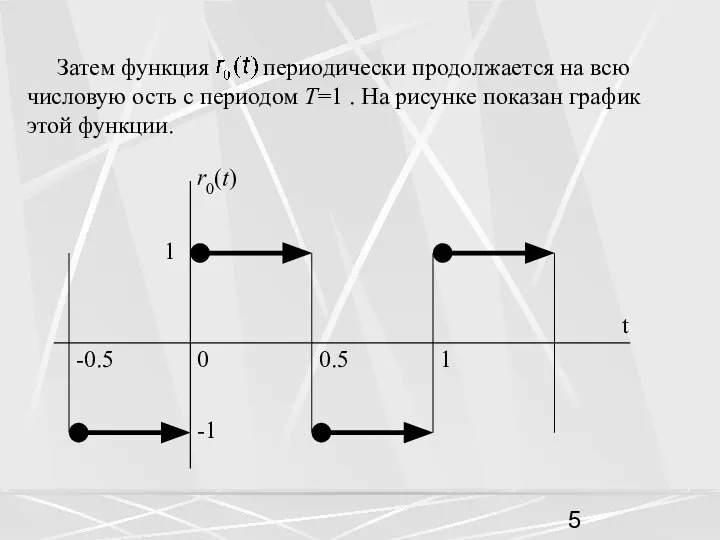
- 5. Затем функция периодически продолжается на всю числовую ость с периодом T=1 . На рисунке показан график
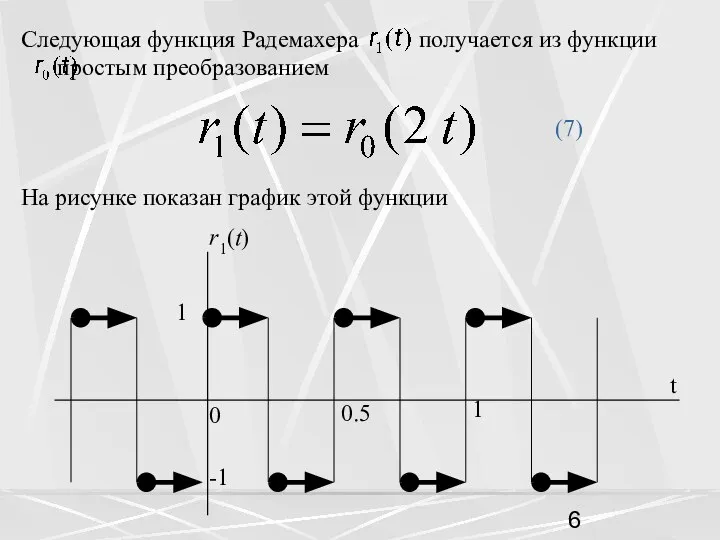
- 6. Следующая функция Радемахера получается из функции простым преобразованием (7) На рисунке показан график этой функции
- 7. Следующая функция Радемахера получается из преобразованием (8) -1
- 8. Как видно график функции получен из графика функции сжатием последнего в четыре раза вдоль оси t
- 9. Свойства системы Функций Радемахера 1) Система функций Радемахера , k=0,1,2,…,∞ ортонормированна на отрезке t∈[0, 1] .
- 10. 2) Система функций Радемахера не является полной. Оказывается можно найти элемент ψ(t) пространства , который не
- 11. Таким образом, система функций Радемахера не может служить базисом в пространстве , т.е. эта система функций
- 12. Система функций Уолша Систему функций Уолша , n=0,1,2,…,∞ определим следующим образом. Представим целое число n ≥
- 13. Тогда функции системы Уолша выражаются при помощи функций Радемахера как (13) Например, для числа n =
- 14. Таким образом, функция Уолша определяется как произведение функций Радемахера с номерами, которые соответствуют единичным индексам в
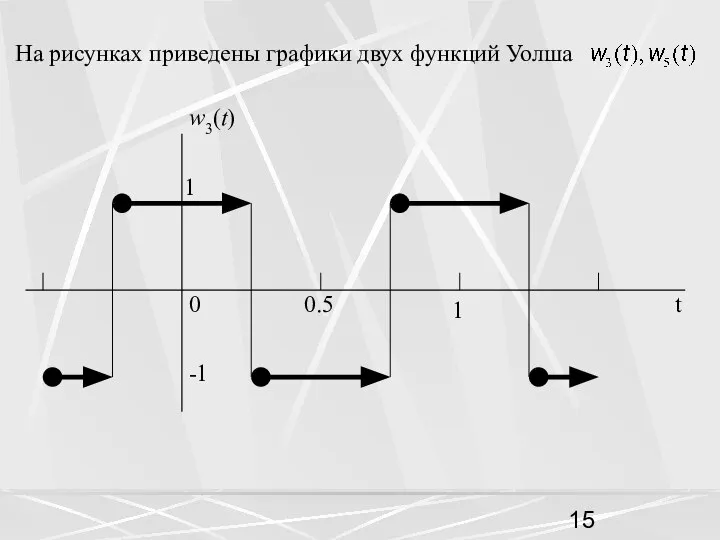
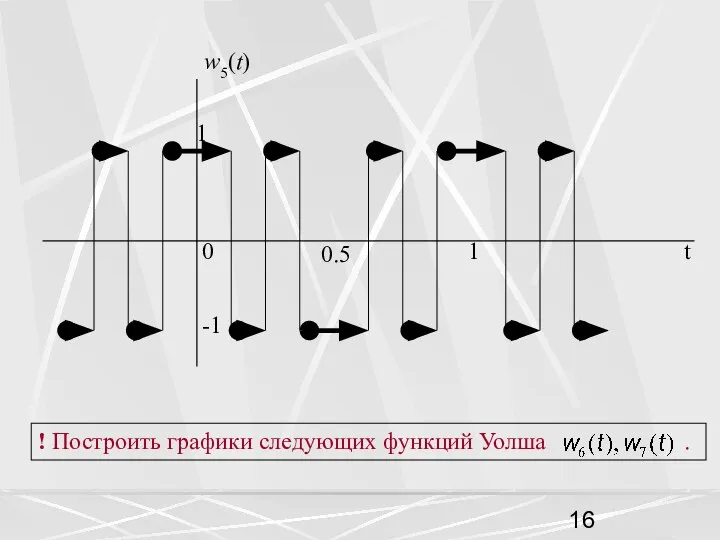
- 15. На рисунках приведены графики двух функций Уолша
- 16. t ! Построить графики следующих функций Уолша .
- 17. Свойства системы Функций Уолша 1) Система функций Уолша , k=0,1,2,…,∞ ортонормированна на отрезке t∈[0, 1]. Поэтому
- 18. Система функций Хаара Систему функций Хаара , n=0,1,2,…,∞ определим на интервале t∈[0, 1) следующим образом. Положим
- 19. Далее введем следующие интервалы. (16)
- 20. Тогда функции Хаара будут определяться следующими соотношениями (17) Например, функция задается соотношениями
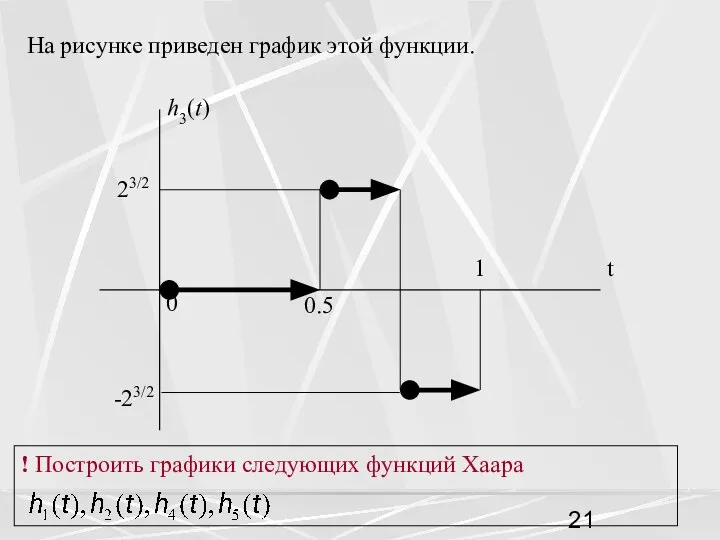
- 21. На рисунке приведен график этой функции. ! Построить графики следующих функций Хаара
- 22. Свойства системы Функций Хаара 1) Система функций Хаара , k=0,1,2,…,∞ ортонормированна на интервале t∈[0, 1]. Поэтому
- 23. Тригонометрические ряды Фурье Рассмотрим тригонометрическую систему функций. (19) Как хорошо известно, из курса специальных разделов математического
- 24. В точках разрыва ряда Фурье сходящегося к среднему значению функции в этих точках. (21) Коэффициенты Фурье
- 25. Свойства тригонометрических рядов Фурье 1) Если функция f(t) четная, то из интегралов (22) видно, что коэффициенты
- 26. 2) Если функция f(t) нечетная, то из интегралов (22) видно, что в этом случае коэффициенты ,
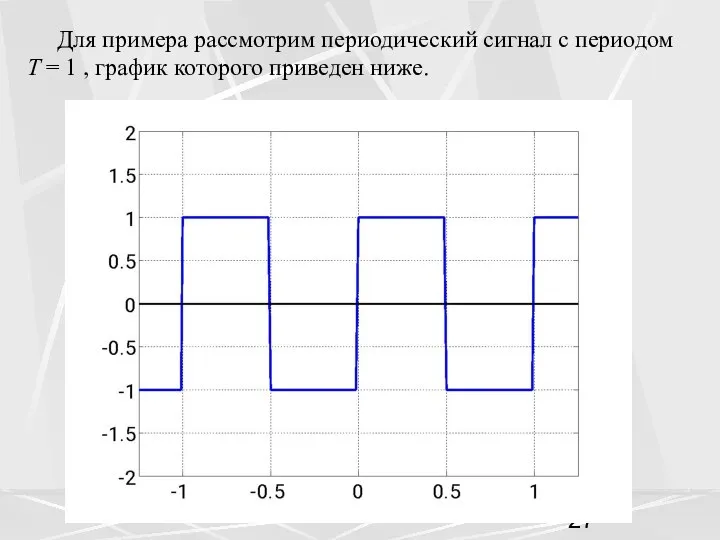
- 27. Для примера рассмотрим периодический сигнал с периодом T = 1 , график которого приведен ниже.
- 28. Функция f(t) описывающая этот сигнал является, во-первых, нечетной функцией, во-вторых, она имеет разрывы в точках t
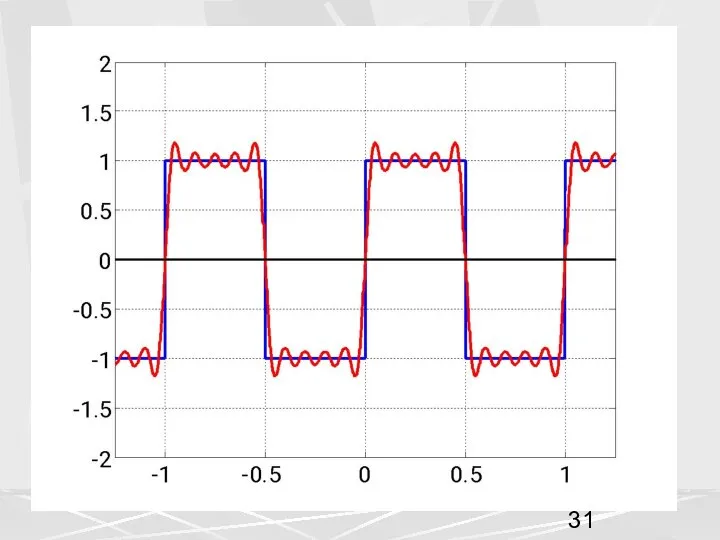
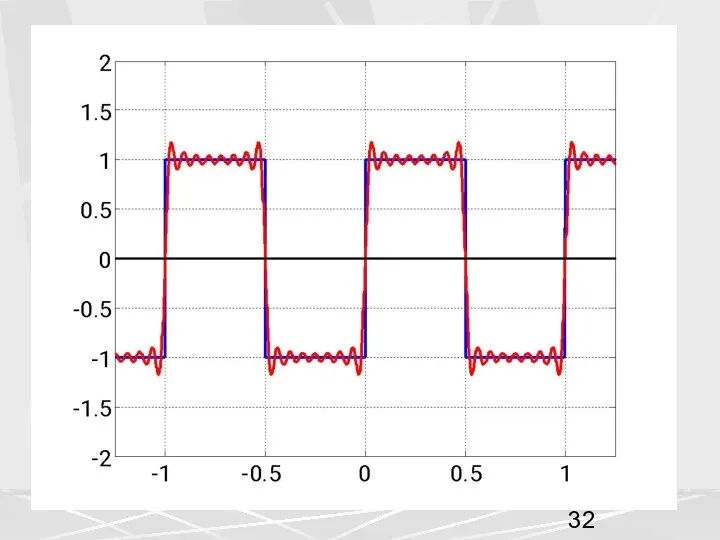
- 33. Отметим следующие свойства ряда Фурье, которые видны из этих графиков 1) С увеличением числа членов N
- 34. 3) Вблизи точек разрыва наблюдаются пульсации, которые не пропадают с увеличением числа членов ряда N ,
- 35. ! Найти коэффициенты ряда Фурье для периодической f(t) функции с периодом T = 1 , и
- 36. Комплексная форма рядов Фурье В радиотехнике наиболее употребительной является комплексная форма ряда Фурье. Эта форма возникает
- 37. Возьмем вещественную форму ряда Фурье (20) и подставим в нее формулы (27). (28) Если ввести следующие
- 38. то ряд Фурье (28) примет вид. (30) где коэффициенты комплексного ряда Фурье будут определяться формулой. (31)
- 39. ! Используя формулы (22) для коэффициентов , вещественного ряда Фурье, показать справедливость формулы (31) для коэффициентов
- 40. Интегральное преобразование Фурье Рассмотрим переход от ряда Фурье в комплексной форме (30, 31) к интегральному преобразованию
- 41. Введем дискретную частоту (33) Тогда расстояние между соседними частотами Δf будет равно (34) Когда период T
- 42. Кроме того, введем функцию от дискретной частоты по формуле (36) Подставляя соотношения (33, 34, 36) в
- 43. Далее в формулах (37) совершаем предельный переход. В результате получаем: (38)
- 44. В математическом анализе доказывается, что преобразование Фурье (38) справедливо для функций s(t) удовлетворяющих следующим условиям. 1)
- 45. Спектральный анализ и преобразование Фурье Кроме временного представления сигналов, где сигнал это функция времени s( t
- 46. Из спектра S( f ) можно получить амплитудно-частотную характеристику (АЧХ) A( f ) и фазово-частотную характеристику
- 47. Здесь звездочка означает комплексное сопряжение. Из этих соотношений видно, что для вещественного сигнала, АЧХ - четная
- 48. Третье, если сигнал вещественная нечетная функция времени , то для спектра выполняются следующие соотношения Здесь действительная
- 49. Сигнал s(t) и его частотный спектр S(f) взаимно однозначно соответствуют друг другу через прямое и обратное
- 50. Свойства преобразования Фурье Кроме рассмотренных выше свойств спектра, преобразование Фурье обладает целым рядом полезных свойств для
- 51. 2) Изменение масштаба. Если у сигнала временной масштаб уменьшается в a раз, то у спектра частотный
- 52. Докажем второе свойство:
- 53. 3) Задержка сигнала. Сдвиг сигнала во времени приводит к умножению спектра на фазовый множитель. ! Доказать
- 54. 4) Свертка сигналов. Сигнал являющийся сверткой двух других сигналов имеет спектр равный произведению спектров исходных сигналов.
- 55. Докажем четвертое свойство:
- 56. 5) Произведение сигналов. Сигнал являющийся произведением двух других сигналов имеет спектр равный свертке спектров исходных сигналов
- 57. 6) Равенство Парсеваля для преобразования Фурье. Для преобразования Фурье имеет место следующее интегральное равенство (равенство Парсеваля).
- 58. 7) Дифференцирование по временной области. Сигнал являющийся производной от другого сигнала имеет спектр равный спектру исходного
- 59. Докажем седьмое свойство, с помощью интегрирования по частям:
- 60. 8) Дифференцирование в частотной области. Сигнал являющийся произведением другого сигнала на время и коэффициент (– 2
- 61. Обобщенное преобразование Фурье Нахождение преобразования Фурье для периодических сигналов вызывает некоторые затруднения. Дело в том, что
- 62. Выход из этого положения состоит в переходе к обобщенному преобразованию Фурье, где используется дельта-функция. Покажем это
- 63. Далее используем интегральное представление дельта-функции. (41) Поэтому спектр сигнала есть суперпозиция дельта-функций.
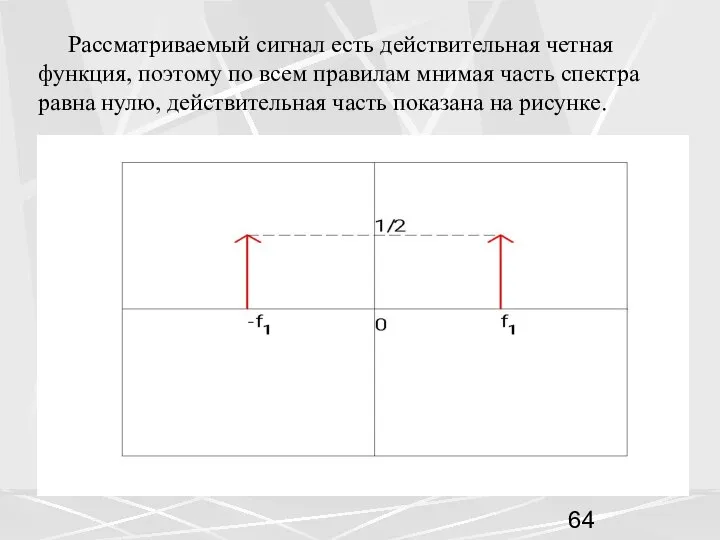
- 64. Рассматриваемый сигнал есть действительная четная функция, поэтому по всем правилам мнимая часть спектра равна нулю, действительная
- 65. Возьмем в качестве гармонического сигнала нечетную функцию. В этом случае получаем следующий спектр сигнала.
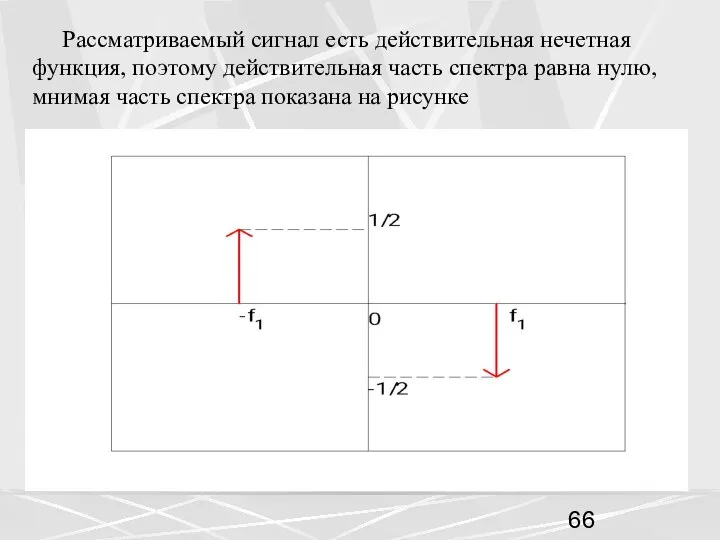
- 66. Рассматриваемый сигнал есть действительная нечетная функция, поэтому действительная часть спектра равна нулю, мнимая часть спектра показана
- 68. Скачать презентацию























































 Имитационное моделирование
Имитационное моделирование Развитие экспериментальной психологии в России
Развитие экспериментальной психологии в России Коми орнамент
Коми орнамент Презентация на тему "Системная подготовка руководителей медицинских организаций" - скачать презентации по Медицине
Презентация на тему "Системная подготовка руководителей медицинских организаций" - скачать презентации по Медицине Выполнили: Мельников Дмитрий, Лукин Максим
Выполнили: Мельников Дмитрий, Лукин Максим 5 физических явлении
5 физических явлении  ЖАНРОВЕ РОЗМАЇТТЯ ДІЛОВИХ КОНТАКТІВ
ЖАНРОВЕ РОЗМАЇТТЯ ДІЛОВИХ КОНТАКТІВ Поздравление с 8 марта
Поздравление с 8 марта 10 things that annoy me!!!
10 things that annoy me!!!  Преобразование графиков функций Учитель математики Шахова Т. А. Гимназия №3 Г. Мурманск
Преобразование графиков функций Учитель математики Шахова Т. А. Гимназия №3 Г. Мурманск Глобальная сеть и интернет
Глобальная сеть и интернет Пролог. Управление поиском решения
Пролог. Управление поиском решения Волосы и ногти
Волосы и ногти  Виды водного транспорта
Виды водного транспорта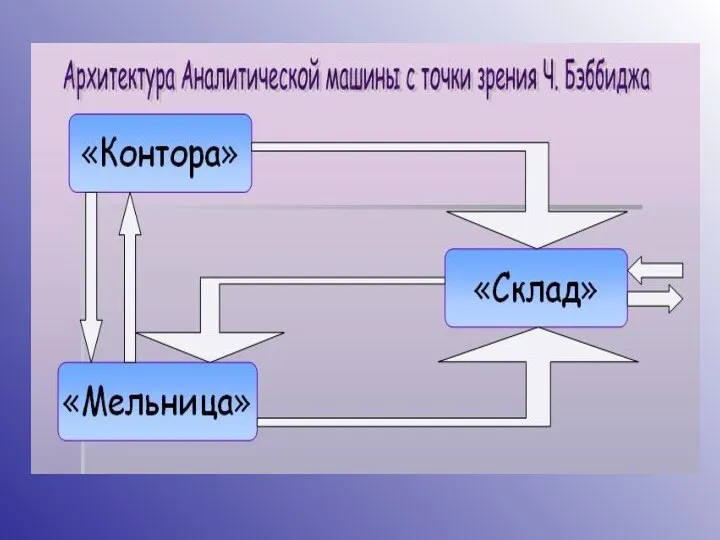 Теоретическая модель магистрально-модульного принципа строения ЭВМ Д. фон Неймана
Теоретическая модель магистрально-модульного принципа строения ЭВМ Д. фон Неймана Презентация: «Философия» Лекция 1. Философия: предмет, проблемы, функции, структура
Презентация: «Философия» Лекция 1. Философия: предмет, проблемы, функции, структура Англия 17-19 века.pptx
Англия 17-19 века.pptx Network Data Model
Network Data Model Игра «Суждения» Выполнили студентки 2 курса ФТД, 1301 Тетеркина Кристина, Анохина Татьяна
Игра «Суждения» Выполнили студентки 2 курса ФТД, 1301 Тетеркина Кристина, Анохина Татьяна  Паралимпийское движение
Паралимпийское движение Устройства ввода: тачпад
Устройства ввода: тачпад Диалектизмы родного села
Диалектизмы родного села . Шурунов В.П. Финансовая грамотность
. Шурунов В.П. Финансовая грамотность Гимнастика как спортивнопедагогическая дисциплина
Гимнастика как спортивнопедагогическая дисциплина Технология производства образцов диоксида урана двух партий.
Технология производства образцов диоксида урана двух партий. Моя профессия - театральная и аудиовизуальная техника
Моя профессия - театральная и аудиовизуальная техника Изобразительные приемы и техники
Изобразительные приемы и техники BTI Systems. Описание решений. Давид Рапопорт. Директор по продажам
BTI Systems. Описание решений. Давид Рапопорт. Директор по продажам