Содержание
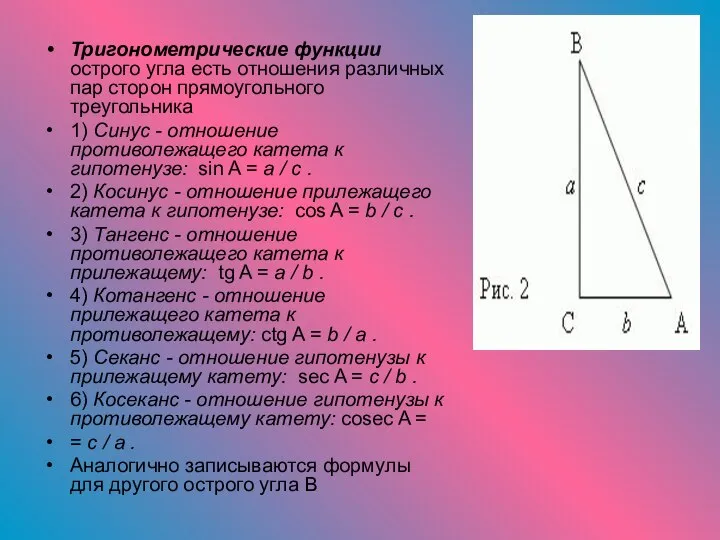
- 2. Тригонометрические функции острого угла есть отношения различных пар сторон прямоугольного треугольника 1) Синус - отношение противолежащего
- 3. П р и м е р : Прямоугольный треугольник ABC ( рис.2 ) имеет катеты: a
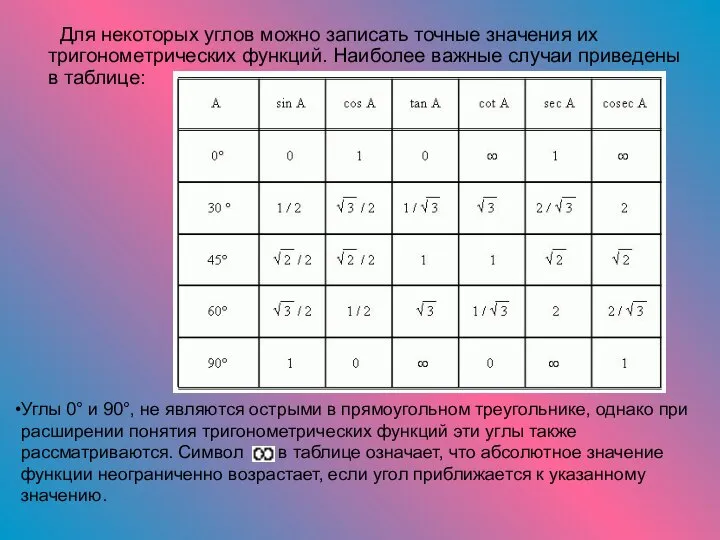
- 4. Для некоторых углов можно записать точные значения их тригонометрических функций. Наиболее важные случаи приведены в таблице:
- 5. Связь тригонометрических функций острого угла
- 6. Тригонометрические функции двойного угла: sin 2x = 2 sinx cosx cos 2x = cos2x - sin2x
- 7. Тригонометрические функции половинного угла Часто бывают полезны формулы, выражающие степени sin и cos простого аргумента через
- 8. Тригонометрические функции суммы углов sin(x+y)= sin x cos y + cos x sin y sin(x-y)= sin
- 9. Для больших значений аргумента можно пользоваться так называемыми формулами приведения, которые позволяют выразить Т. ф. любого
- 10. Важнейшими тригонометрическими формулами являются формулы сложения, выражающие Т. ф. суммы или разности значений аргумента через Т.
- 11. Производные всех Тригонометрических функций выражаются через Тригонометрические функции
- 12. График функции y = sinx имеет вид:
- 13. График функции y = cosx имеет вид:
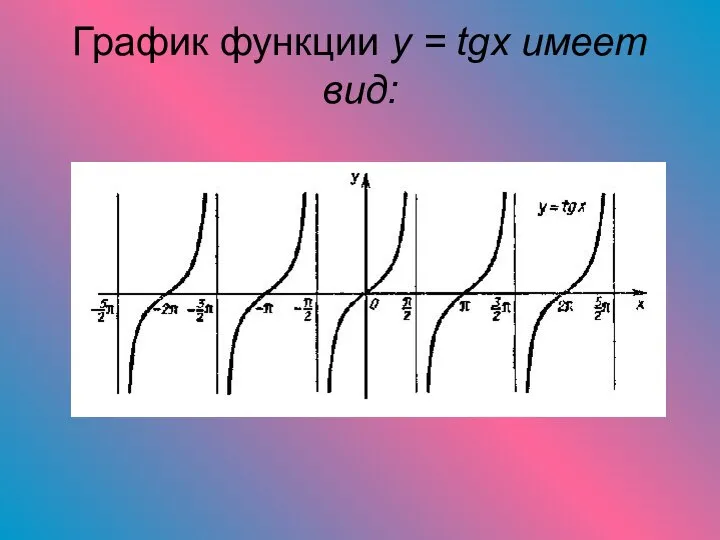
- 14. График функции y = tgx имеет вид:
- 15. График функции y = ctgx имеет вид:
- 16. История возникновения тригонометрических функций Т. ф. возникли впервые в связи с исследованиями в астрономии и геометрии.
- 18. Скачать презентацию












 Презентация на тему ИЗГОТОВЛЕНИЕ ВЫКРОЕК
Презентация на тему ИЗГОТОВЛЕНИЕ ВЫКРОЕК  Работа над словом на уроках русского языка - презентация для начальной школы
Работа над словом на уроках русского языка - презентация для начальной школы Реформирование и деятельность ОВД Советского государства 1945-1991 гг
Реформирование и деятельность ОВД Советского государства 1945-1991 гг Анализ и оптимизация бизнес-процессов. Лекция 5
Анализ и оптимизация бизнес-процессов. Лекция 5 Квазиэлектронные АТС
Квазиэлектронные АТС Модель Митчелла и Хауса
Модель Митчелла и Хауса Понятие Cookie
Понятие Cookie Анималотерапия - презентация для начальной школы_
Анималотерапия - презентация для начальной школы_ черпные нервы
черпные нервы Общеразвивающие упражнения в гимнастике и их характеристика
Общеразвивающие упражнения в гимнастике и их характеристика Телеоло́гия
Телеоло́гия  Электронные компоненты для монтажа на печатные платы
Электронные компоненты для монтажа на печатные платы Ценные бумаги
Ценные бумаги Качество как объект управления. Лекция 2
Качество как объект управления. Лекция 2 Презентация Таможенные платежи, специальные, антидемпинговые, компенсационные пошлины
Презентация Таможенные платежи, специальные, антидемпинговые, компенсационные пошлины Електроємність. Конденсатори та їх використання в техніці. Енергія електричного поля
Електроємність. Конденсатори та їх використання в техніці. Енергія електричного поля Пневмонии и гнойные заболевания лёгких. Этиология. Клиника. Диагностика. Осложнения. Основные принципы лечения Доцент Т.Ю.Че
Пневмонии и гнойные заболевания лёгких. Этиология. Клиника. Диагностика. Осложнения. Основные принципы лечения Доцент Т.Ю.Че Характеристика животных Обмен веществами животного с внешней средой. Базальный метаболизм
Характеристика животных Обмен веществами животного с внешней средой. Базальный метаболизм Самоконтроль при занятиях физкультурой
Самоконтроль при занятиях физкультурой Маркетинговые исследования Эксперимент
Маркетинговые исследования Эксперимент  Культура Византии
Культура Византии Русская матрёшка
Русская матрёшка Prezi.com Юлия Рачинская
Prezi.com Юлия Рачинская Кейс «Тайленол» на основе материалов Effie Awards
Кейс «Тайленол» на основе материалов Effie Awards Презентация "Северный экономический район (природа и население)" - скачать презентации по Экономике
Презентация "Северный экономический район (природа и население)" - скачать презентации по Экономике Критика снизу вверх
Критика снизу вверх Обеспечение обязательств Подготовил: студент Группы Ю092 Виноградская Екатерина
Обеспечение обязательств Подготовил: студент Группы Ю092 Виноградская Екатерина Российский государственный социальный университет Тадж-Махал Памятник любви и красоты.
Российский государственный социальный университет Тадж-Махал Памятник любви и красоты.