Содержание
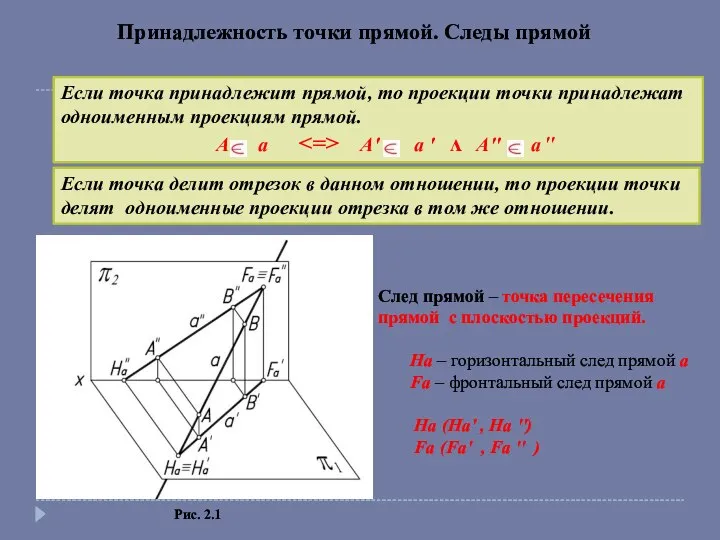
- 2. Принадлежность точки прямой. Следы прямой Если точка принадлежит прямой, то проекции точки принадлежат одноименным проекциям прямой.
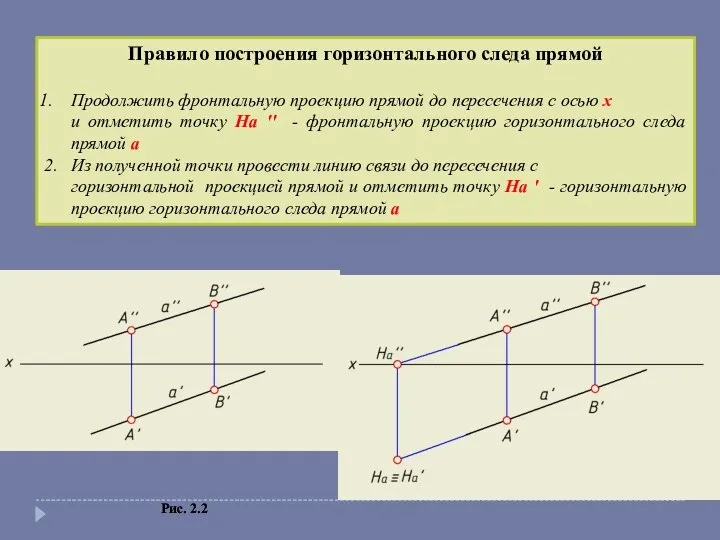
- 3. Правило построения горизонтального следа прямой Продолжить фронтальную проекцию прямой до пересечения с осью x и отметить
- 4. Правило построения фронтального следа прямой Продолжить горизонтальную проекцию прямой a до пересечения с осью x и
- 5. Рис. 2.3 Рис. 2.4 ПРЯМЫЕ ЧАСТНОГО ПОЛОЖЕНИЯ Прямые уровня – прямые, параллельные плоскостям проекций Горизонтальная прямая
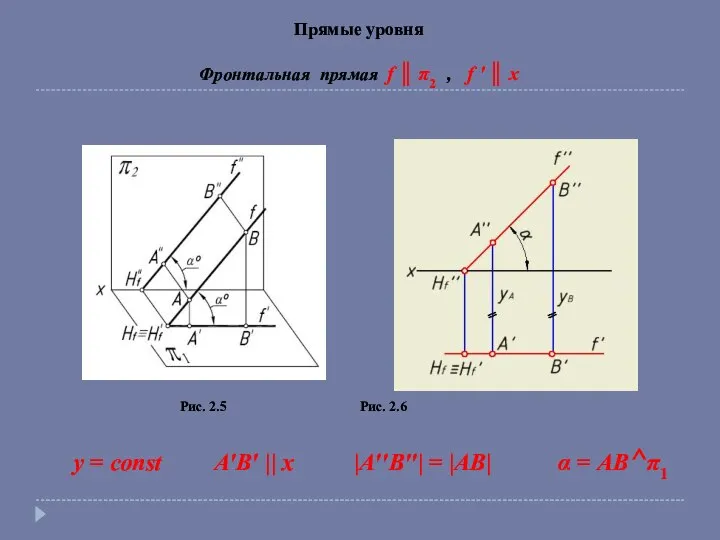
- 6. Прямые уровня Фронтальная прямая f ║ π2 , f ' ║ x Рис. 2.5 Рис. 2.6
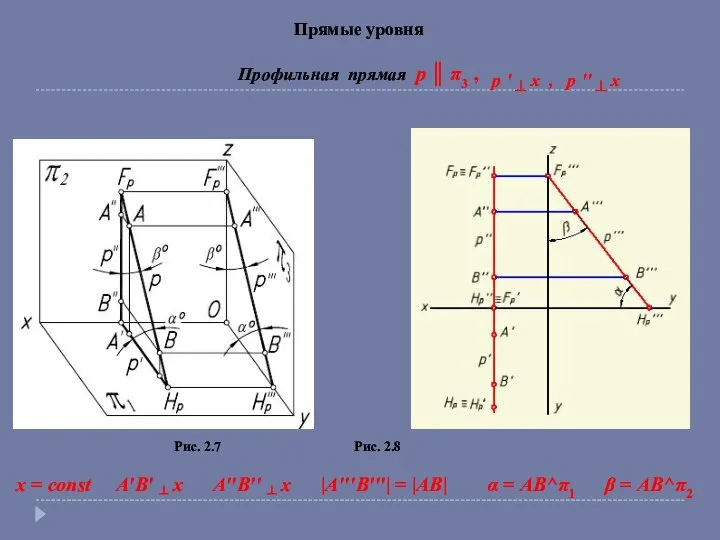
- 7. Прямые уровня Профильная прямая p ║ π3 , Рис. 2.7 Рис. 2.8 p ' ┴ x
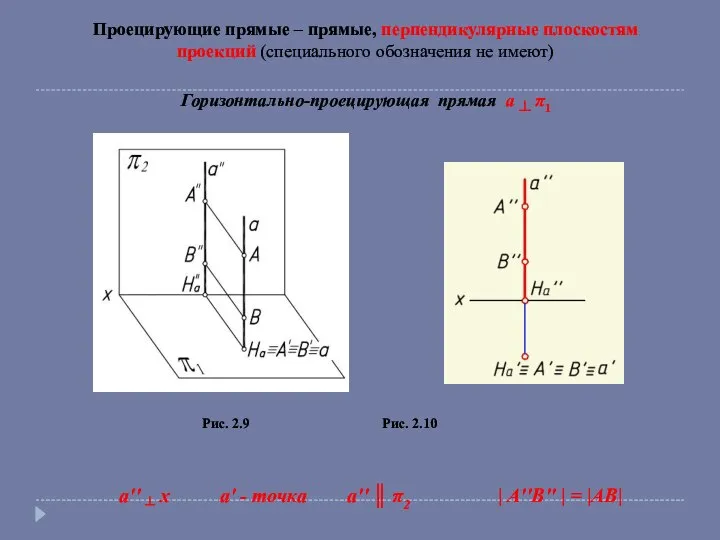
- 8. Проецирующие прямые – прямые, перпендикулярные плоскостям проекций (специального обозначения не имеют) Горизонтально-проецирующая прямая a ┴ π1
- 9. Проецирующие прямые Фронтально-проецирующая прямая a ┴ π2 Рис. 2.11 Рис. 2.12 a′ ┴ x a′′ -
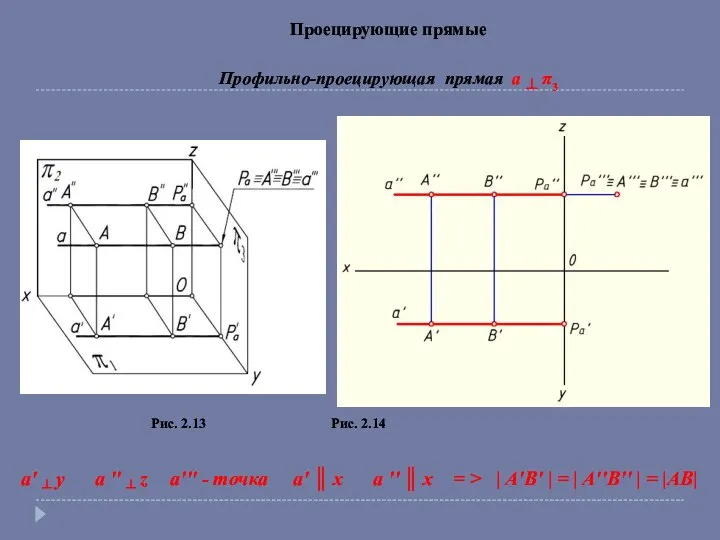
- 10. Проецирующие прямые Профильно-проецирующая прямая a ┴ π3 Рис. 2.13 Рис. 2.14 a′ ┴ y a ′′
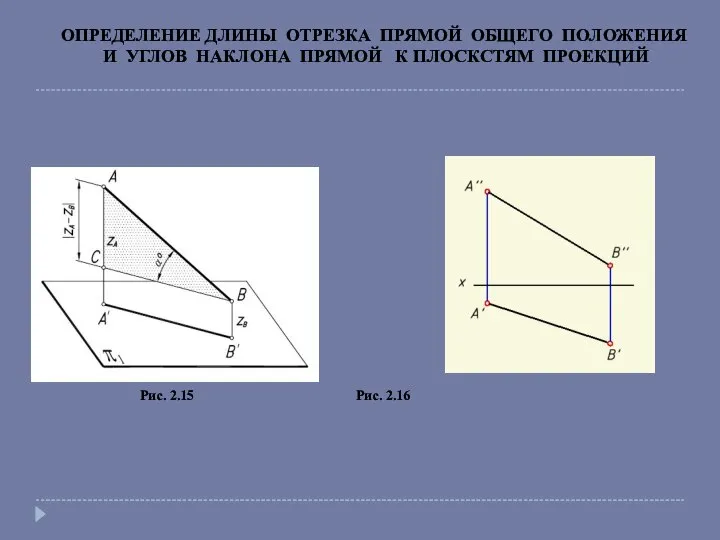
- 11. ОПРЕДЕЛЕНИЕ ДЛИНЫ ОТРЕЗКА ПРЯМОЙ ОБЩЕГО ПОЛОЖЕНИЯ И УГЛОВ НАКЛОНА ПРЯМОЙ К ПЛОСКСТЯМ ПРОЕКЦИЙ Отрезок прямой общего
- 12. ОПРЕДЕЛЕНИЕ ДЛИНЫ ОТРЕЗКА ПРЯМОЙ ОБЩЕГО ПОЛОЖЕНИЯ И УГЛОВ НАКЛОНА ПРЯМОЙ К ПЛОСКСТЯМ ПРОЕКЦИЙ Рис. 2.15 Рис.
- 13. Правило определения длины отрезка общего положения и углов наклона его к плоскостям проекций Построить прямоугольный треугольник,
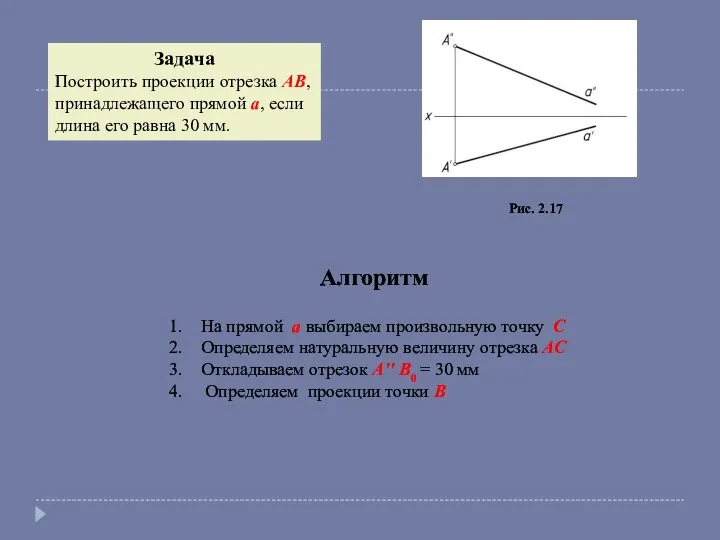
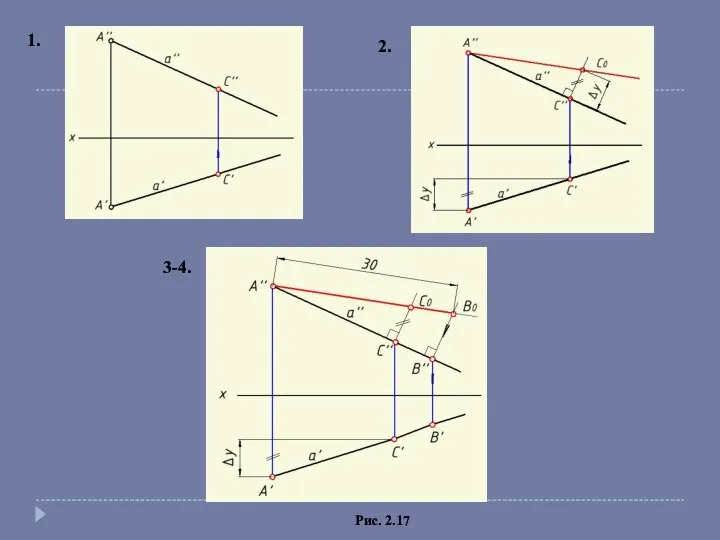
- 14. Рис. 2.17 Алгоритм На прямой a выбираем произвольную точку C Определяем натуральную величину отрезка AC Откладываем
- 15. Рис. 2.17 1. 2. 3-4.
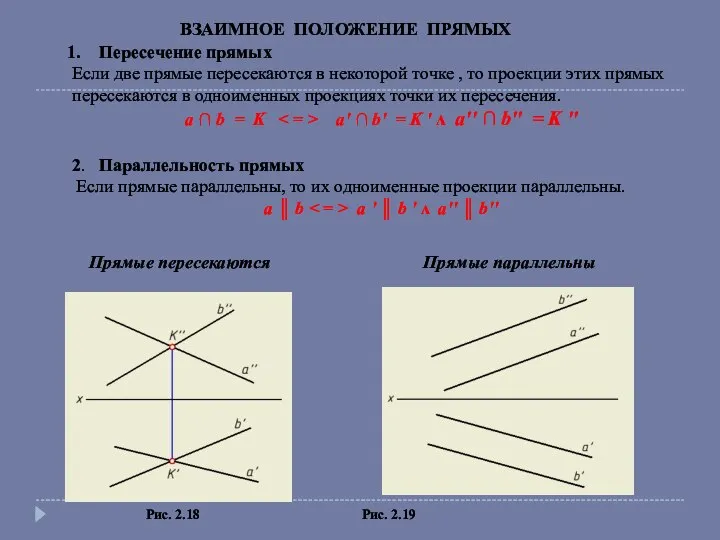
- 16. ВЗАИМНОЕ ПОЛОЖЕНИЕ ПРЯМЫХ Рис. 2.18 Рис. 2.19 Прямые пересекаются Прямые параллельны Пересечение прямых Если две прямые
- 17. Скрещивание прямых Скрещивающиеся прямые – не параллельны и не пересекаются, т. е. не лежат в одной
- 19. Скачать презентацию






 Управление и организация SA-P. Процесс работы
Управление и организация SA-P. Процесс работы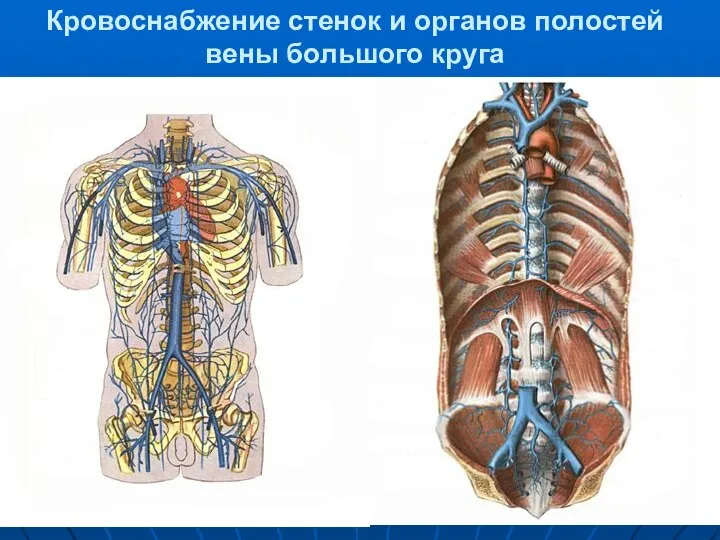 Кровоснабжение стенок и органов полостей
Кровоснабжение стенок и органов полостей  Время норма глубина осушения и междренные расстояния
Время норма глубина осушения и междренные расстояния Sakramenty święte
Sakramenty święte Жизнь и творчество Дмитрия Емца
Жизнь и творчество Дмитрия Емца Презентация Экология Задача
Презентация Экология Задача Методы экспертных оценок в системном анализе
Методы экспертных оценок в системном анализе Аттестационная работа. «Топонимика и балтинизмы Лыткарино и окрестностей»
Аттестационная работа. «Топонимика и балтинизмы Лыткарино и окрестностей» Предоставление прав медицинским бюджетным учреждениям
Предоставление прав медицинским бюджетным учреждениям Наркомания
Наркомания Романтизм в западноевропейской живописи
Романтизм в западноевропейской живописи Протезирование включенных дефектов переднего отдела зубных рядов
Протезирование включенных дефектов переднего отдела зубных рядов  Как помочь ребенку справиться со стрессом во время ЕГЭ (Памятка организатору)
Как помочь ребенку справиться со стрессом во время ЕГЭ (Памятка организатору) Семейство SIMATIC S7
Семейство SIMATIC S7 Государственная гражданская служба
Государственная гражданская служба Основные свойства и применение проводниковых материалов
Основные свойства и применение проводниковых материалов Розробка плати балансування та заряду для li-io акумуляторів
Розробка плати балансування та заряду для li-io акумуляторів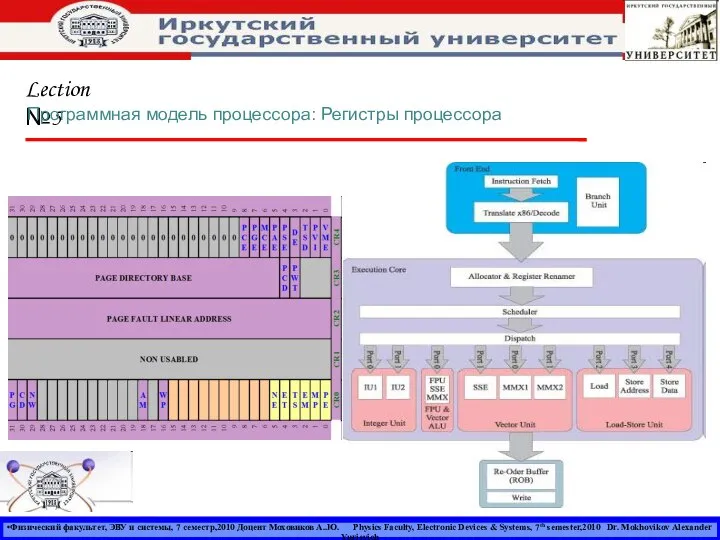 регистры проц
регистры проц Презентация Международные стандарты социального обеспечения в странах Южной Америки
Презентация Международные стандарты социального обеспечения в странах Южной Америки  Lesevorschriften, sprachtraining
Lesevorschriften, sprachtraining Казнить нельзя, помиловать. Смертная казнь
Казнить нельзя, помиловать. Смертная казнь Противопаразитарные
Противопаразитарные Презентация "Профессия Экономист" - скачать презентации по Экономике
Презентация "Профессия Экономист" - скачать презентации по Экономике بخش مسابقه ای طراحان کسب و کار جشنواره ملی فنآفرینی شیخبهایی
بخش مسابقه ای طراحان کسب و کار جشنواره ملی فنآفرینی شیخبهایی Кодирование информации
Кодирование информации  Свенский Свято-Успенский монастырь
Свенский Свято-Успенский монастырь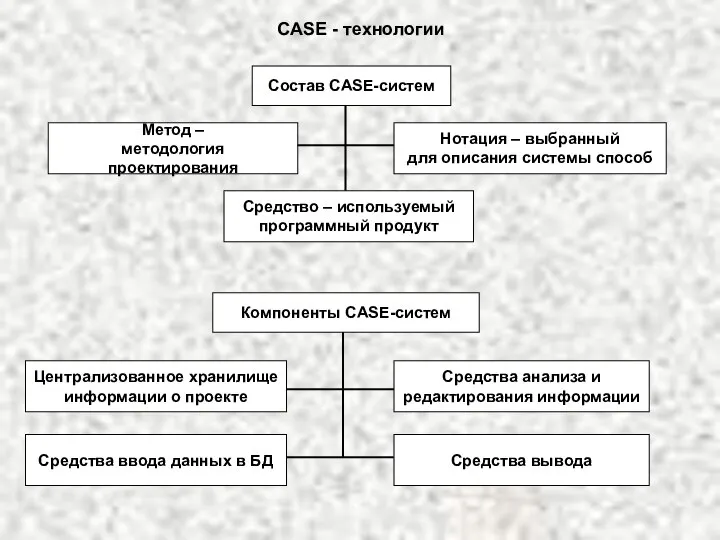 Case технология
Case технология  Табун
Табун