Содержание
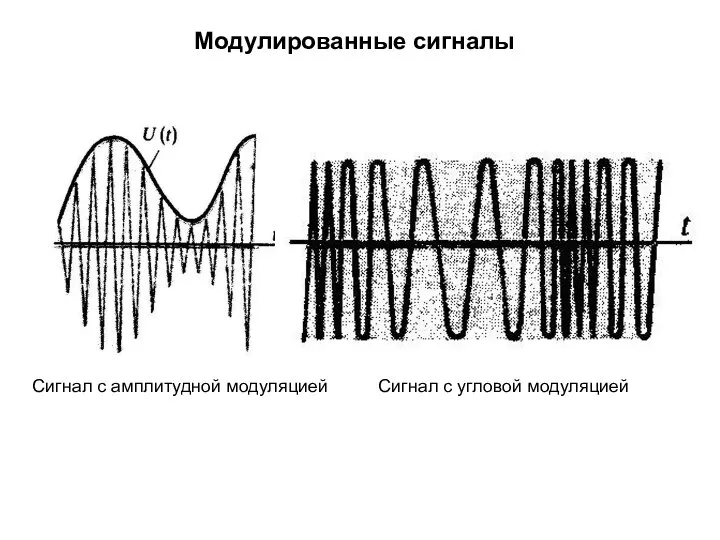
- 2. Модулированные сигналы Сигнал с угловой модуляцией Сигнал с амплитудной модуляцией
- 3. Сигналы с угловой модуляцией В несущем гармоническом колебании передаваемое сообщение s(t) изменяет либо частоту , либо
- 4. Виды угловой модуляции. Фазовая модуляция Пусть полная фаза связана с сигналом s(t) зависимостью где — значение
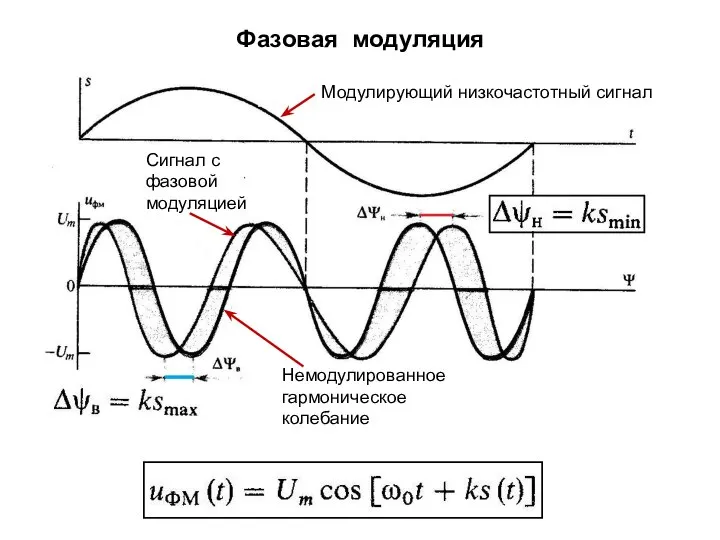
- 5. Фазовая модуляция Модулирующий низкочастотный сигнал Немодулированное гармоническое колебание Сигнал с фазовой модуляцией
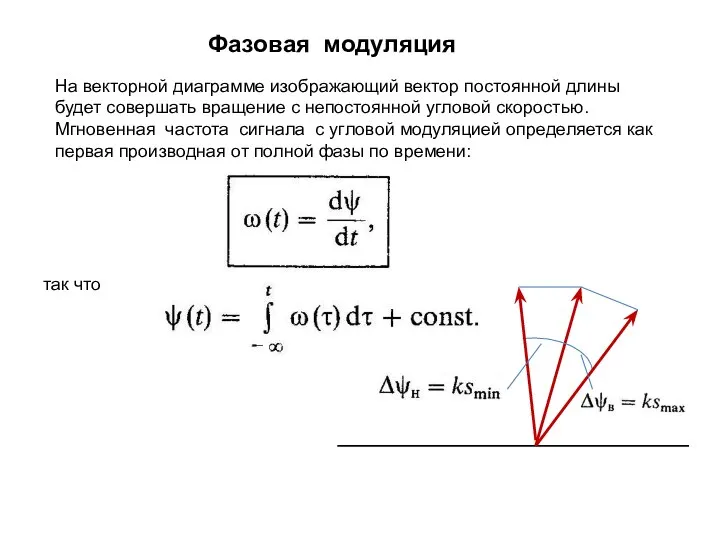
- 6. Фазовая модуляция так что На векторной диаграмме изображающий вектор постоянной длины будет совершать вращение с непостоянной
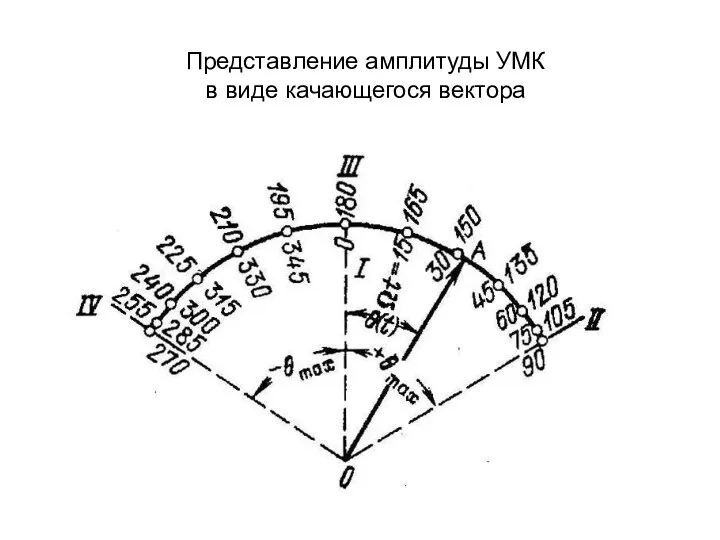
- 7. Представление амплитуды УМК в виде качающегося вектора
- 8. Виды угловой модуляции. Частотная модуляция При частотной модуляции сигнала (ЧМ) между величинами s(t) и имеется связь
- 9. Виды угловой модуляции Если s(t) — достаточно гладкая функция, то внешне осциллограммы ФМ- и ЧМ-сигналов не
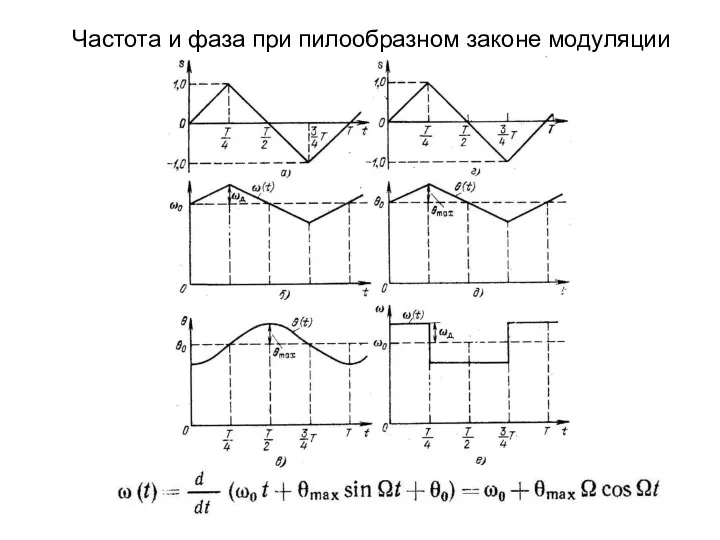
- 10. Частота и фаза при пилообразном законе модуляции
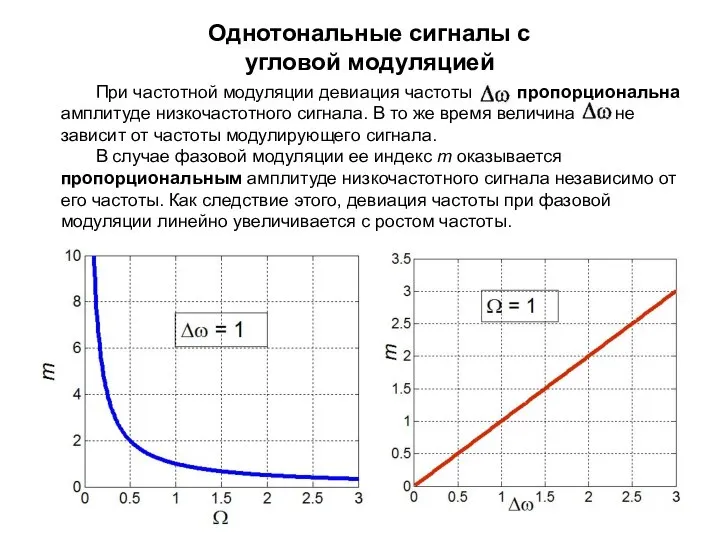
- 11. Однотональные сигналы с угловой модуляцией Анализ ФМ- и ЧМ-сигналов с математической точки зрения гораздо сложнее, чем
- 12. Однотональные сигналы с угловой модуляцией При частотной модуляции девиация частоты пропорциональна амплитуде низкочастотного сигнала. В то
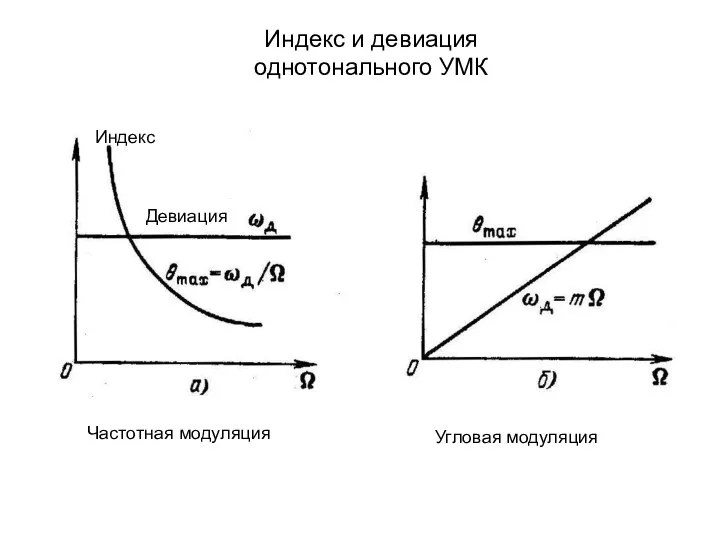
- 13. Индекс и девиация однотонального УМК Индекс Девиация Частотная модуляция Угловая модуляция
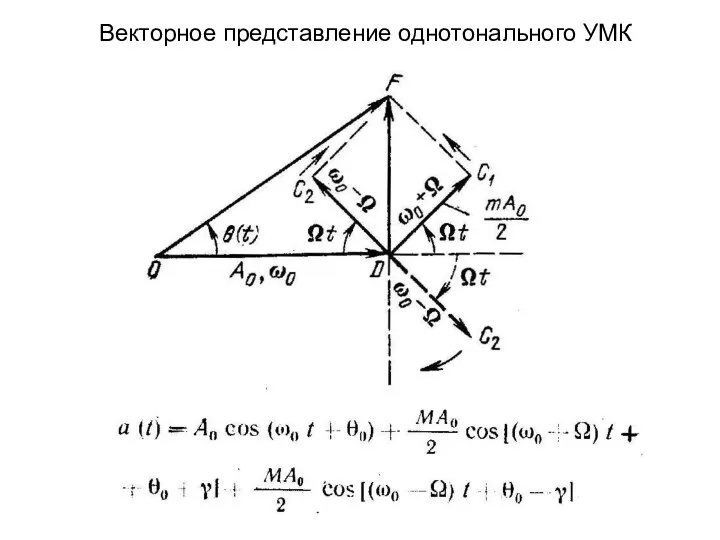
- 14. Векторное представление однотонального УМК
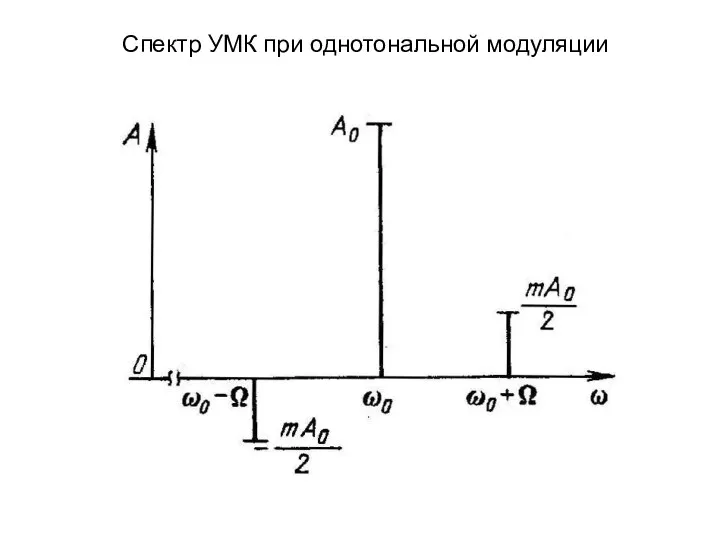
- 15. Спектр УМК при однотональной модуляции
- 16. Пример Радиостанция, работающая в УКВ-диапазоне с несущей частотой fo= 80 МГц, излучает ФМ-сигнал, промодулированный частотой F
- 17. Спектральное разложение ЧМ- и ФМ-сигналов при малых индексах модуляции Представим ЧМ-сигнал в виде суммы гармонических колебаний,
- 18. Спектральное разложение ЧМ- и ФМ-сигналов при малых индексах модуляции В спектре сигнала с угловой модуляцией содержатся
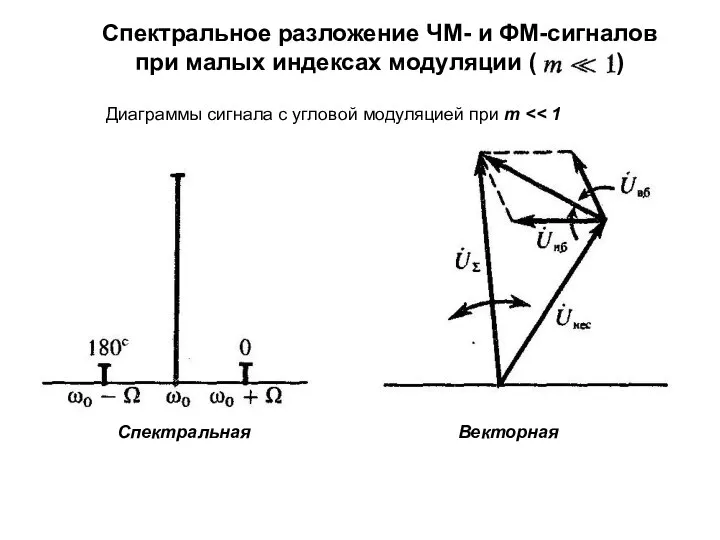
- 19. Спектральное разложение ЧМ- и ФМ-сигналов при малых индексах модуляции ( ) Векторная Диаграммы сигнала с угловой
- 20. Более точный вид спектрального состава сигналов с угловой модуляцией В спектре сигнала с однотональной угловой модуляцией,
- 21. Более точный вид спектральной диаграммы
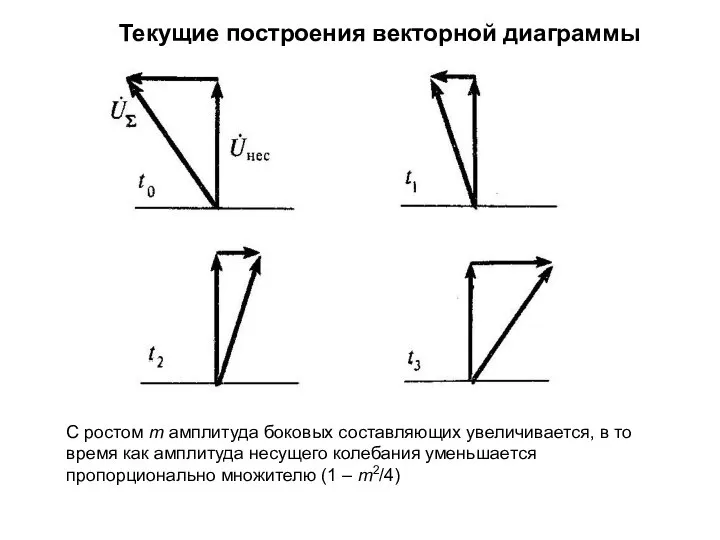
- 22. Текущие построения векторной диаграммы С ростом m амплитуда боковых составляющих увеличивается, в то время как амплитуда
- 23. Спектр сигнала с угловой модуляцией при произвольном значении индекса m Для простейшего случая однотонального ЧМ- или
- 24. Спектр сигнала с угловой модуляцией при произвольном значении индекса m Отсюда получаем следующую математическую модель ЧМ-или
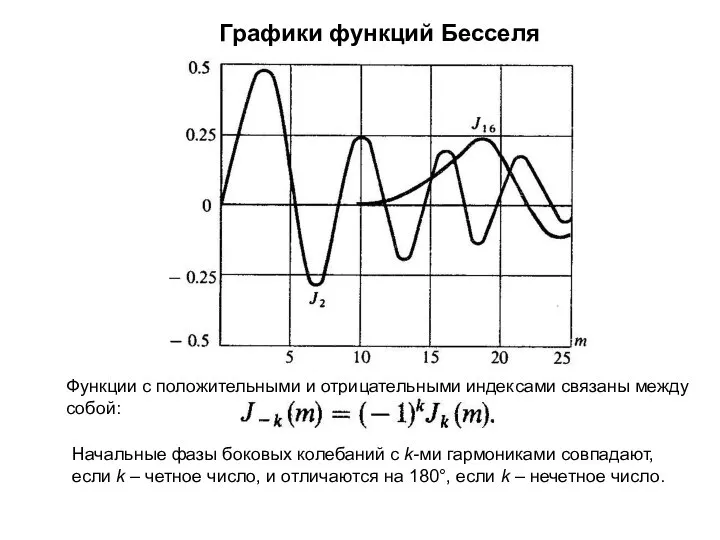
- 25. Графики функций Бесселя Функции с положительными и отрицательными индексами связаны между собой: Начальные фазы боковых колебаний
- 26. Ширина спектра сигнала с угловой модуляцией при произвольном значении индекса m Можно заметить следующее: чем больше
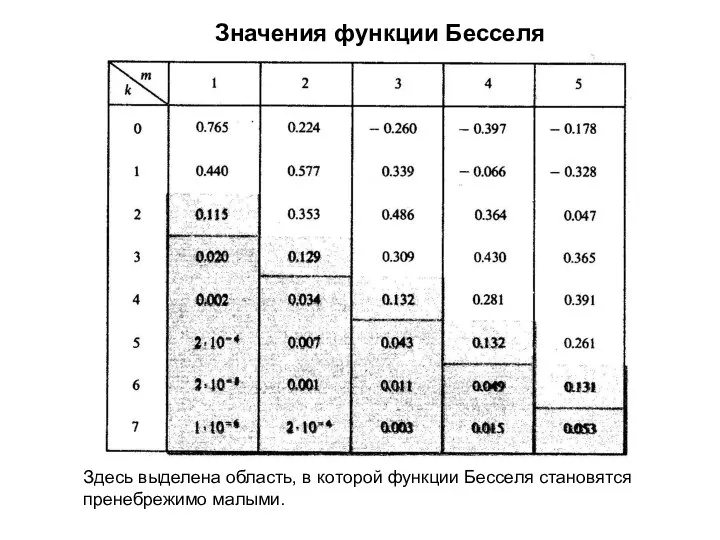
- 27. Значения функции Бесселя Здесь выделена область, в которой функции Бесселя становятся пренебрежимо малыми.
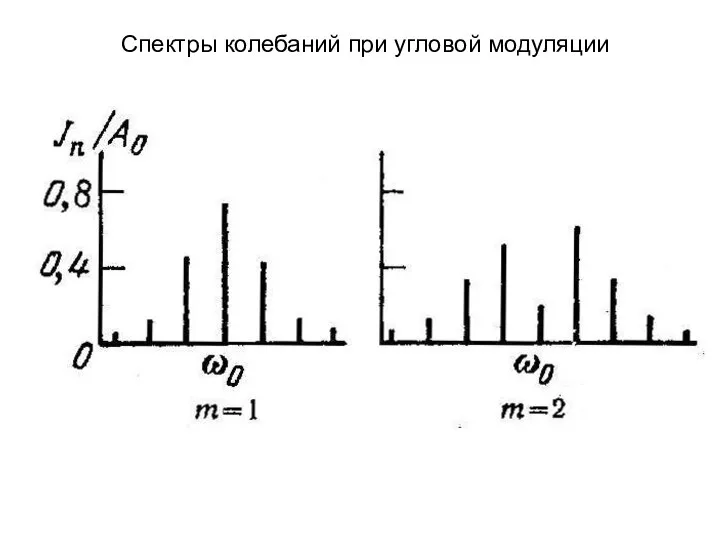
- 28. Спектры колебаний при угловой модуляции
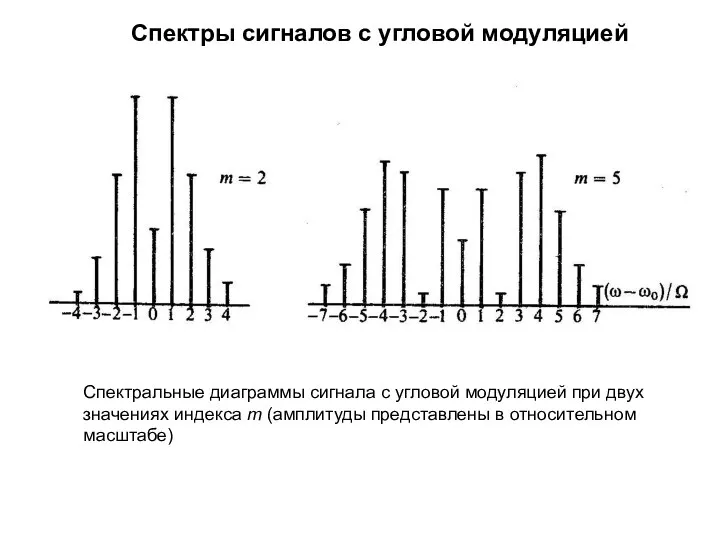
- 29. Спектры сигналов с угловой модуляцией Спектральные диаграммы сигнала с угловой модуляцией при двух значениях индекса m
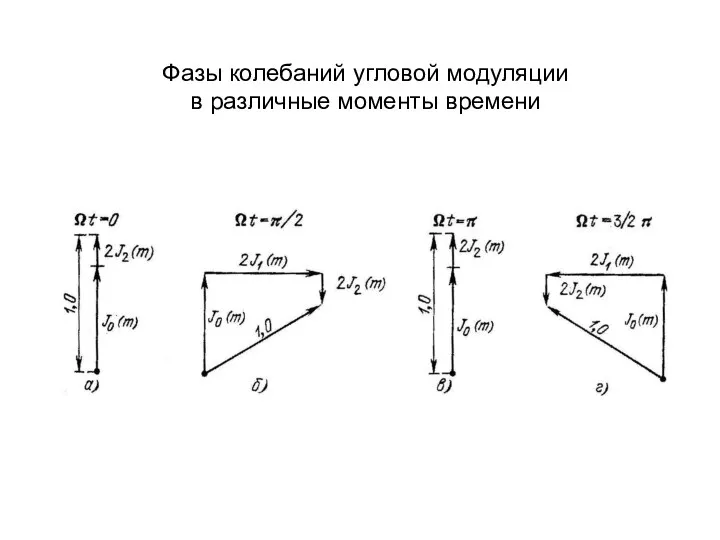
- 30. Фазы колебаний угловой модуляции в различные моменты времени
- 31. Мощность в спектре угловых колебаний Рост индекса модуляции приводит к перераспределению мощности в спектре модулированного сигнала.
- 32. Пример Однотональный ЧМ-сигнал имеет девиацию частоты = 240 кГц. Найти частоты модуляции F, при которых несущее
- 33. Угловая модуляция при двух гармонических модулирующих сигналах Рассмотрим для простоты сигнал, промодулированный по частоте лишь двумя
- 34. Угловая модуляция при двух гармонических модулирующих сигналах Следует обратить внимание на то, что в спектре рассматриваемого
- 35. Спектр ЧМ-модуляции при двух гармонических модулирующих сигналах Следует обратить внимание на то, что в спектре рассматриваемого
- 36. Спектр ЧМ-модуляции в общем случае Таким образом, при прочих равных условиях спектр колебания со сложной угловой
- 38. Скачать презентацию



















 Воздушные вяжущие материалы
Воздушные вяжущие материалы Использование техники объемной лепки в изготовлении традиционной русской новогодней игрушки из ваты
Использование техники объемной лепки в изготовлении традиционной русской новогодней игрушки из ваты Interdependence between migration and terrorism within the EU borders
Interdependence between migration and terrorism within the EU borders Модернизация стран Востока, перспективы процесса
Модернизация стран Востока, перспективы процесса Кто такой инвестор и как с ним договариваться Мария Саулина Директор портала biznesbomba.ru. - презентация
Кто такой инвестор и как с ним договариваться Мария Саулина Директор портала biznesbomba.ru. - презентация Религия во время Великой Отечественной войны
Религия во время Великой Отечественной войны Аттестационная работа. Памятники религиозной культуры города Нижнекамск
Аттестационная работа. Памятники религиозной культуры города Нижнекамск Школьный портфель Мир верх ногами
Школьный портфель Мир верх ногами Презентация на тему "Использование современных образовательных технологий в начальной школе" - скачать презентации по Педаг
Презентация на тему "Использование современных образовательных технологий в начальной школе" - скачать презентации по Педаг Автор: Банникова Алёна, 6 класс, Объединение «Волшебный краснотал» Педагог Н.В.Бородина
Автор: Банникова Алёна, 6 класс, Объединение «Волшебный краснотал» Педагог Н.В.Бородина Оригами из модулей
Оригами из модулей Типы автоматических коробок передач
Типы автоматических коробок передач Директорские часы ГБОУ лицей №623 30.11.2014 года Актовый зал
Директорские часы ГБОУ лицей №623 30.11.2014 года Актовый зал ЗАДАНИЕ ПО ФУНКЦИЯМ МЕНЕДЖМЕНТА
ЗАДАНИЕ ПО ФУНКЦИЯМ МЕНЕДЖМЕНТА Пеппи в стране Веселии - презентация для начальной школы
Пеппи в стране Веселии - презентация для начальной школы Лекарственные средства, влияющие на систему крови
Лекарственные средства, влияющие на систему крови  Обработка одномерных массивов
Обработка одномерных массивов Берлитион
Берлитион  Репка - презентация для начальной школы
Репка - презентация для начальной школы День матери
День матери Орындаған: Құмарбекова Н.Е Қабылдаған: Қожекенова Ж.А. Топ: 10-011-02қ Факультет: жалпы медицина
Орындаған: Құмарбекова Н.Е Қабылдаған: Қожекенова Ж.А. Топ: 10-011-02қ Факультет: жалпы медицина Достопримечательности США
Достопримечательности США Технологические процессы в строительстве
Технологические процессы в строительстве Спринг-эластика. Начни себя в гимнастике
Спринг-эластика. Начни себя в гимнастике Дитяча експлуатація
Дитяча експлуатація Великие гуманисты Европы
Великие гуманисты Европы Дауысты дыбыстар
Дауысты дыбыстар Основы проектирования и оснащения производства
Основы проектирования и оснащения производства