Распределения дискретных и непрерывных случайных величин и их числовые характеристики.

Содержание

Слайд 2

Литература и интернет - ресурсы Вентцель Е.С., Овчаров Л.А. Задачи и

Литература и интернет - ресурсы

Вентцель Е.С., Овчаров Л.А. Задачи и упражнения

по теории вероятностей: учебное пособие. М.: Академия, 2003. – 448 с.
Гмурман В.Е. Теория вероятностей и математическая статистика: Учеб. пособие. – М.: Высшее образование, 2006. – 479 с.
Гмурман В.Е. Руководство к решению задач по теории вероятностей и математическая статистика: Учеб. пособие. – М.: Высшее образование, 2006. – 404 с.
Колмогоров А.Н. Основные понятия теории вероятностей. М.: Фазис, 1998. – 144 с.
http://e-lib.uspu.ru
www.exponenta.ru
Слайд 3

Введение. Дискретные и непрерывные случайные величины Определение: Случайной называют величину, которая

Введение. Дискретные и непрерывные случайные величины

Определение: Случайной называют величину, которая в

результате испытания принимает значение − единственное, заранее неизвестное и зависящее от случайных причин, которые заранее не могут быть учтены.
Случайные величины (с.в.) принято обозначать большими буквами латинского алфавита (X, Y, Z, …), а значения, ими принимаемые – малыми (x, y, z, …). Например, если с.в. величина X принимает три значения, их обозначают x1, x2, x3.
Определение: Дискретной называют случайную величину (д.с.в.), которая принимает отдельные, изолированные возможные значения с определенными вероятностями. Число возможных значений д.с.в. может быть конечным или счетным.
Определение: Непрерывной называют случайную величину (н.с.в.), которая принимает непрерывный ряд значений из некоторого конечного или бесконечного промежутка. Число возможных значений н.с.в. бесконечно и несчетно.
Слайд 4

§1. Распределения дискретных случайных величин и их числовые характеристики Определение: Законом

§1. Распределения дискретных случайных величин и их числовые характеристики

Определение: Законом распределения

дискретной случайной величины (д.с.в.) называют соответствие между ее возможными значениями и их вероятностями. Такое соответствие может быть задано таблично, аналитически (в виде формулы), графически.
Определение: Дискретным рядом распределения д.с.в. называется таблица, в которой перечислены (как правило, упорядоченно) все возможные значения д.с.в. и соответствующие им вероятности:
Прим. Значения д.с.в. не повторяются: xi ≠ xj при i ≠ j.
Д.с.в. X принимает с необходимостью одно из множества значений {x1, x2, …, xn}. События X = x1, X = x2, …, X = xn образуют полную группу. Поэтому с необходимостью: p1 + p2 + … + pn = 1.
Слайд 5

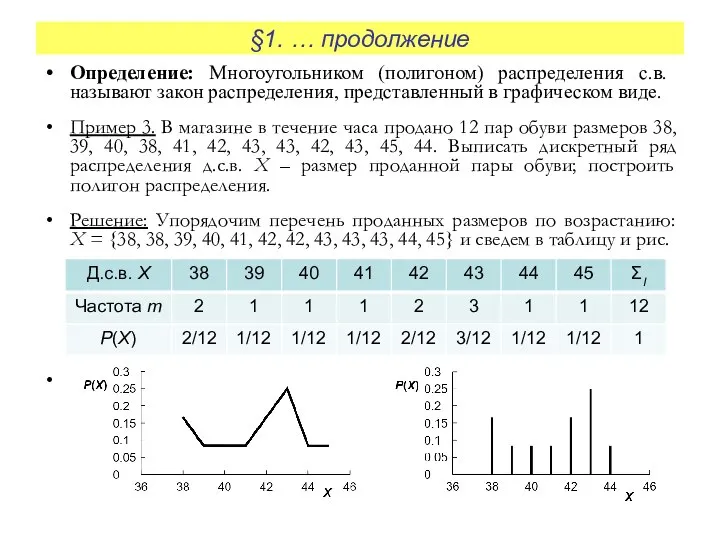
§1. … продолжение Определение: Многоугольником (полигоном) распределения с.в. называют закон распределения,

§1. … продолжение

Определение: Многоугольником (полигоном) распределения с.в. называют закон распределения, представленный

в графическом виде.
Пример 3. В магазине в течение часа продано 12 пар обуви размеров 38, 39, 40, 38, 41, 42, 43, 43, 42, 43, 45, 44. Выписать дискретный ряд распределения д.с.в. X – размер проданной пары обуви; построить полигон распределения.
Решение: Упорядочим перечень проданных размеров по возрастанию: X = {38, 38, 39, 40, 41, 42, 42, 43, 43, 43, 44, 45} и сведем в таблицу и рис.
Слайд 6

§1. … продолжение Определение: Модой распределения называют значение xi, соответствующее максимуму

§1. … продолжение

Определение: Модой распределения называют значение xi, соответствующее максимуму закона

(ряда) распределения.
Определение: Если (явно выделяющаяся) мода одна − распределение называют унимодальным; если моды две – бимодальным и т.д.
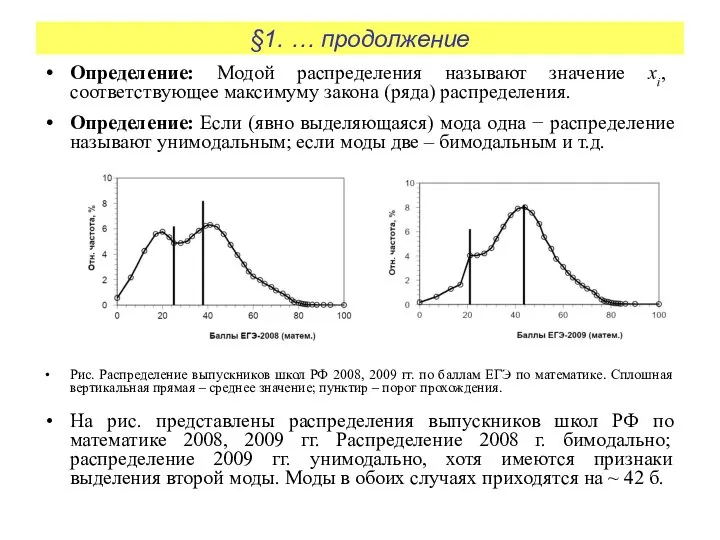
Рис. Распределение выпускников школ РФ 2008, 2009 гг. по баллам ЕГЭ по математике. Сплошная вертикальная прямая – среднее значение; пунктир – порог прохождения.
На рис. представлены распределения выпускников школ РФ по математике 2008, 2009 гг. Распределение 2008 г. бимодально; распределение 2009 гг. унимодально, хотя имеются признаки выделения второй моды. Моды в обоих случаях приходятся на ~ 42 б.
Слайд 7

§1. … продолжение. Биномиальное распределение Определение: Биномиальным называют распределение вероятностей, определяемое

§1. … продолжение. Биномиальное распределение

Определение: Биномиальным называют распределение вероятностей, определяемое формулой

Бернулли (0 ≤ k ≤ n, q = 1 – p):
Pn(k) = Cnk⋅pk⋅qn−k.
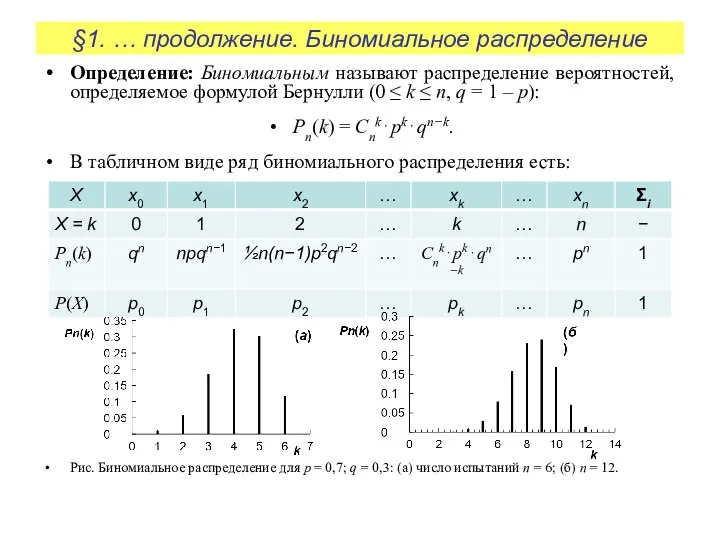
В табличном виде ряд биномиального распределения есть:
Рис. Биномиальное распределение для p = 0,7; q = 0,3: (а) число испытаний n = 6; (б) n = 12.
Слайд 8

§1. … продолжение. Распределение Пуассона Определение: Распределением Пуассона называют распределение вероятностей,

§1. … продолжение. Распределение Пуассона

Определение: Распределением Пуассона называют распределение вероятностей, определяемое

формулой Пуассона (n⋅p = λ = Const):
Pn(k) = (λk/k!)⋅e−λ, k = 0, 1, 2, …
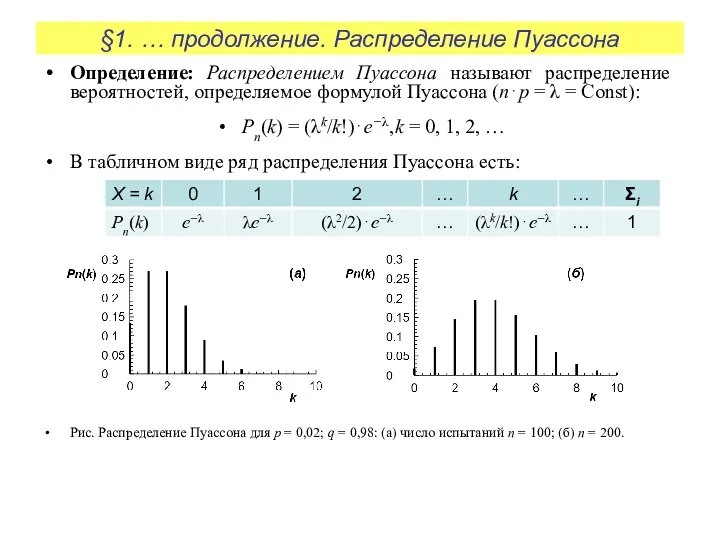
В табличном виде ряд распределения Пуассона есть:
Рис. Распределение Пуассона для p = 0,02; q = 0,98: (а) число испытаний n = 100; (б) n = 200.
Слайд 9

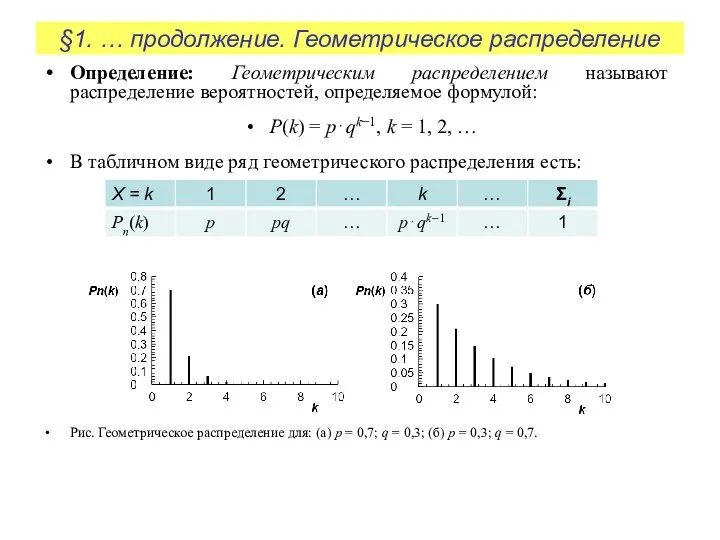
§1. … продолжение. Геометрическое распределение Определение: Геометрическим распределением называют распределение вероятностей,

§1. … продолжение. Геометрическое распределение

Определение: Геометрическим распределением называют распределение вероятностей, определяемое

формулой:
P(k) = p⋅qk−1, k = 1, 2, …
В табличном виде ряд геометрического распределения есть:
Рис. Геометрическое распределение для: (а) p = 0,7; q = 0,3; (б) p = 0,3; q = 0,7.
Слайд 10

§1. … продолжение. Числовые характеристики распределения дискретной случайной величины Определение: Числовыми

§1. … продолжение. Числовые характеристики распределения дискретной случайной величины

Определение: Числовыми характеристиками

(распределения) случайной величины называется набор чисел, обобщенно характеризующих закон распределения этой с.в. (мода, математическое ожидание, дисперсия, СКО и др.)
Определение: Математическим ожиданием дискретной случайной величины (д.с.в.) X называют сумму произведений всех ее возможных значений на соответствующие вероятности:
M(X) = Σi xi⋅pi = x1⋅p1 + x2⋅p2 + …. + xn⋅pn.
Пример 4. Найти математическое ожидание числа очков, выпадающих при бросании игральной кости.
Решение: Закон распределения д.с.в. X – число выпавших очков при бросании игральной кости является равномерным:
Математическое ожидание д.с.в. X равно:
M(X) = Σi xi⋅pi = 1⋅ + 2⋅ + 3⋅ + 4⋅ + 5⋅ + 6⋅ = 3,5.
Ответ: M(X) = 3,5.
Слайд 11

§1. … продолжение. Числовые характеристики распределения дискретной случайной величины Пример 5.

§1. … продолжение. Числовые характеристики распределения дискретной случайной величины

Пример 5. Найти

математическое ожидание суммы очков, выпадающих при бросании пары игральных костей.
Решение: Закон распределения д.с.в. X – сумма выпавших очков при бросании пары игральных костей является треугольным (см. табл. и рис.):
Математическое ожидание д.с.в. X равно:
M(X) = Σi xi⋅pi = (1/36)⋅(2⋅1 + 3⋅2 + 4⋅3 + … + 10⋅3 + 11⋅2 + 12⋅1) = 7.
Ответ: M(X) = 7.
Слайд 12

§1. … продолжение. Свойства математического ожидания Вероятностно-статистический смысл математического ожидания. Пусть

§1. … продолжение. Свойства математического ожидания

Вероятностно-статистический смысл математического ожидания.
Пусть произведено

n испытаний, в которых д.с.в. X приняла m1 раз значение x1, m2 раз значение x2, …, mk раз значение xk; при этом:
m1 + m2 + … + mk = n.
Определение: Средним арифметическим Xср д.с.в. X называют величину:
Xср = {x1⋅m1 + x2⋅m2 + … + xk⋅mk},
или
Xср = x1⋅w1 + x2⋅w2 + … + xk⋅wk,
где относительные частоты есть w1 = m1/n; w2 = m2/n; …; wk = mk/n.
При большом числе испытаний (n → ∞) относительные частоты стремятся к соответствующим вероятностям (закон больших чисел): w1 → p1; w2 → p2; …; wk → pk. Поэтому при больших n:
Xср ≈ x1⋅p1 + x2⋅p2 + … + xk⋅pk = M(X).
Утверждение. Математическое ожидание приближенно равно (тем точнее, чем больше n) среднему арифметическому наблюдаемых значений д.с.в. В этом и состоит вероятностно – статистический смысл математического ожидания.
Слайд 13

§1. … продолжение. Свойства математического ожидания Свойство 1. Математическое ожидание (М.О.)

§1. … продолжение. Свойства математического ожидания

Свойство 1. Математическое ожидание (М.О.) постоянной

величины равно самой этой постоянной:
M(C) = C.
Док-во: СРС.
Свойство 2. Постоянный множитель можно выносить за знак М.О.:
M(CX) = CM(X).
Док-во: СРС.
Свойство 3. М.О. произведения двух независимых случайных величин равно произведению их математических ожиданий:
M(XY) = M(X)⋅M(Y).
Док-во: СРС.
Свойство 4. М.О. суммы двух случайных величин равно сумме их математических ожиданий:
M(X + Y) = M(X) + M(Y).
Док-во: СРС.
Слайд 14

§1. … продолжение. Свойства дисперсии и среднеквадратического отклонения (СКО) Определение: Отклонением

§1. … продолжение. Свойства дисперсии и среднеквадратического отклонения (СКО)

Определение: Отклонением называют

разность между с.в. X и ее математическим ожиданием M(X) :
ΔX = X − M(X).
Для отклонения ΔX закон распределения имеет вид:
Прим. Величину ΔX = X − M(X) также называют центрированной величиной.
Теорема. Математическое ожидание отклонения равно нулю:
M(ΔX) = M(X − M(X)).
Док-во: СРС.
Определение: Дисперсией (рассеянием) D(X) случайной величины называют математическое ожидание квадрата ее отклонения от математического ожидания:
D(X) = M(ΔX2) = M((X − M(X))2).
Слайд 15

§1. … продолжение. Свойства дисперсии и среднеквадратического отклонения (СКО) Для квадрата

§1. … продолжение. Свойства дисперсии и среднеквадратического отклонения (СКО)

Для квадрата отклонения

ΔX2 закон распределения имеет вид:
Дисперсия D(X) с.в. может быть найдена по формуле:
D(X) = M((X − M(X))2) =
= p1⋅(x1 − M(X))2 + p2⋅(x2 − M(X))2 + … + pn⋅(xn − M(X))2.
Теорема (формула вычисления дисперсии). Дисперсия равна разности между М.О. квадрата с.в. X и квадратом ее математического ожидания:
D(X) = M(X2) − (M(X))2 = M(X2) − M2(X).
Док-во: Для доказательства достаточно выписать цепочку равенств, следующую из свойств математического ожидания:
D(X) = M((X − M(X))2) = M(X2 −2X⋅M(X) + M2(X)) = M(X2) − M2(X), ч.т.д.
Слайд 16

§1. … продолжение. Свойства дисперсии и среднеквадратического отклонения (СКО) Свойство 1.

§1. … продолжение. Свойства дисперсии и среднеквадратического отклонения (СКО)

Свойство 1. Дисперсия

постоянной величины равна нулю:
D(C) = 0.
Док-во: СРС.
Свойство 2. Постоянный множитель можно выносить за знак дисперсии, возведя его в квадрат:
D(CX) = C2⋅D(X).
Док-во: Достаточно применить формулу вычисления дисперсии:
D(CX) = M((СX)2) − (M(СX))2 = M(С2X2) − (СM(X))2 =
= С2⋅M(X2) − С2⋅(M(X))2 = С2⋅[M(X2) − M2(X)] = C2⋅D(X), ч.т.д.
Свойство 3. Дисперсия суммы двух независимых случайных величин равна сумме их дисперсий:
D(X + Y) = D(X) + D(Y).
Док-во: По определению дисперсии:
D(X + Y) = M((X + Y)2)−(M(X + Y))2 = M(X2 +2XY + Y2)−(M(X) + M(Y))2 = = M(X2)+2M(XY ) + M(Y2) − M2(X) + 2M(X)⋅M(Y) + M2(Y) = D(X) + D(Y), ч.т.д.
Слайд 17

§1. … продолжение. Свойства дисперсии и среднеквадратического отклонения (СКО) Свойство 4.

§1. … продолжение. Свойства дисперсии и среднеквадратического отклонения (СКО)

Свойство 4. Дисперсия

разности двух независимых случайных величин равна сумме их дисперсий:
D(X − Y) = D(X) + D(Y).
Док-во: По доказанным свойствам дисперсии:
D(X − Y) = D(X + (−1)⋅Y) = D(X)+ D((−1)⋅Y)) = D(X)+ D((−1)⋅Y)) =
= D(X)+ (−1)2⋅ D(Y)) = D(X) + D(Y), ч.т.д.
Замечание: Дисперсия как мера разброса значений с.в. X не слишком удобна, т.к. имеет размерность квадрата с.в. С этой точки зрения более удобна величина, называемая средним квадратичным (квадратическим) отклонением (СКО); в западной терминологии СКО называют также стандартным отклонением.
Определение: Средним квадратичным отклонением (СКО) случайной величины X называют квадратный корень из дисперсии этой с.в.:
σ(X) = √D(X).
Замечание: Свойства СКО σ(X) непосредственно вытекают из соответствующих свойств дисперсии D(X) случайной величины X.
Слайд 18

§1. … продолжение. Свойства дисперсии и среднеквадратического отклонения (СКО) Теорема. Среднее

§1. … продолжение. Свойства дисперсии и среднеквадратического отклонения (СКО)

Теорема. Среднее квадратичное

отклонение суммы конечного числа взаимно независимых случайных величин равно квадратному корню из суммы квадратов СКО этих величин:
σ(X1 + X2 + …+ Xn) = √{σ2(X1) + σ2(X2) + … + σ2(Xn)}.
Док-во: По доказанным свойствам дисперсии:
σ(X1 + X2 + …+ Xn) = √D(X1 + X2 + …+ Xn) =
= √{D(X1) + D(X2) +…+ D(Xn)} = √{σ2(X1) + σ2(X2) +…+ σ2(Xn)}, ч.т.д.
Теорема. Пусть имеется система из n независимых д.с.в. X1, X2, …, Xn, которые имеют одинаковые распределения, т.е. равные М.О., дисперсии и СКО: a(X1) = a(X2) = … = a(Xn) = a; D(X1) = D(X2) = … = D(Xn) = σ2; σ(X1) = σ(X2) = … = σ(Xn) = σ. Тогда М.О., дисперсия и СКО среднего арифметического этих с.в., соответственно, равны:
M(Xср) = M[(X1 + X2 + … + Xn)] = a;
D(Xср) = D[(X1 + X2 + … + Xn)] =  σ2;
σ(Xср) = σ[(X1 + X2 + … + Xn)] = σ/√n.
Док-во: СРС.
Слайд 19

§2. Распределения непрерывных случайных величин и их числовые характеристики Определение: (Интегральной)

§2. Распределения непрерывных случайных величин и их числовые характеристики

Определение: (Интегральной) функцией

распределения называют функцию F(X), определяющая вероятность того, что случайная величина X в результате испытания примет значения, меньшее x, т.е.
F(X) = P(X < x).
Определение: Непрерывной называют случайную величину (н.с.в.) функция распределения которой является непрерывной, кусочно-гладкой функцией с кусочно-непрерывной производной.
Свойство 1. Значения функции распределения принадлежат промежутку [0; 1], т.е. F(x) изменяется в диапазоне 0 ≤ F(x) ≤ 1.
Док-во: СРС.
Свойство 2. Функции распределения является F(x) неубывающей:
F(x1) ≤ F(x2) при x1 ≤ x2.
Док-во: СРС.
Следствие 1. Вероятность того, что с.в. X примет значения X ∈ [a; b]:
P(a ≤ X < b) = F(b) − F(a).
Следствие 2. Вероятность того, что с.в. X примет конкретное фиксированное значение X = a равна нулю.
Слайд 20

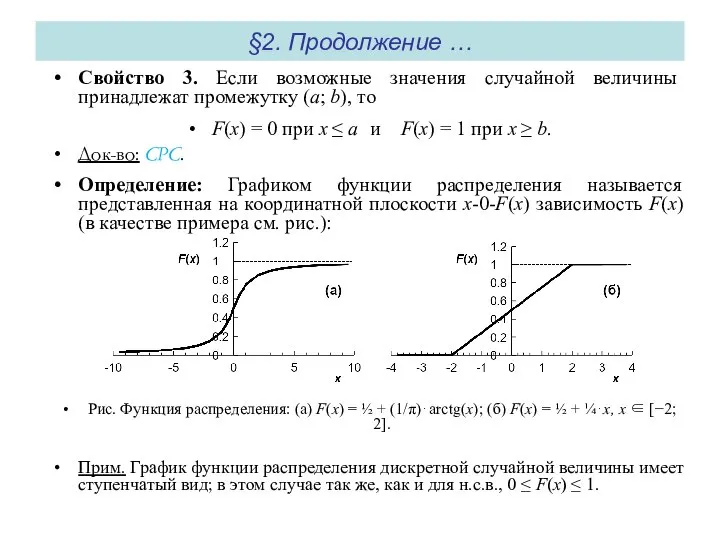
§2. Продолжение … Свойство 3. Если возможные значения случайной величины принадлежат

§2. Продолжение …

Свойство 3. Если возможные значения случайной величины принадлежат промежутку

(a; b), тo
F(x) = 0 при x ≤ a и F(x) = 1 при x ≥ b.
Док-во: СРС.
Определение: Графиком функции распределения называется представленная на координатной плоскости x-0-F(x) зависимость F(x) (в качестве примера см. рис.):
Рис. Функция распределения: (а) F(x) = ½ + (1/π)⋅arctg(x); (б) F(x) = ½ + ¼⋅x, x ∈ [−2; 2].
Прим. График функции распределения дискретной случайной величины имеет ступенчатый вид; в этом случае так же, как и для н.с.в., 0 ≤ F(x) ≤ 1.
Слайд 21

§2. Продолжение … Определение. Плотностью функции распределения (ПФР) вероятностей (дифференциальной функцией

§2. Продолжение …

Определение. Плотностью функции распределения (ПФР) вероятностей (дифференциальной функцией распределения)

функцию f(x) − первую производную интегральной функции F(x):
f(x) = F′(x).
Следствие. По плотности распределения f(x) путем интегрирования можно восстановить функцию распределения F(x):
x
F(x) = ∫ f(x)dx.
−∞
Прим. Для дискретной случайной величины понятие плотности функции распределения f(x) не определено.
Теорема. Вероятность того, что н.с.в. X примет значения X ∈ [a; b) может быть найдена интегрированием от a до b:
b
P(a ≤ X < b) = ∫ f(x)dx.
a
Прим. Геометрически это соответствует нахождению площади под графиком ПФР f(x) на промежутке [a; b).
Слайд 22

§2. Продолжение … Определение: График ПФР f(x) называют кривой распределения (вероятностей).

§2. Продолжение …

Определение: График ПФР f(x) называют кривой распределения (вероятностей).
Сформулируем свойства

плотности функции распределения f(x).
Свойство 1. Плотность функции распределения f(x) неотрицательная функция.
Док-во: Функция распределения F(x) – неубывающая функция. Поэтому ее производная F′(x) неотрицательна, ч.т.д.
Свойство 2. Несобственный интеграл от плотности распределения f(x) в пределах от −∞ до +∞ равен единице (условие нормировки):
+∞
∫ f(x)dx = 1.
−∞
Свойство 3 (вероятностный смысл плотности распределения). Вероятность того, что случайная величина X примет значение, принадлежащее интервалу (x; x + dx), равна произведению плотности вероятности f(x) в точке x на ширину этого интервала dx:
dP(X) = F(x + dx) − F(x) = f(x)dx.
Слайд 23

§2. Продолжение …

§2. Продолжение …

 

Слайд 24

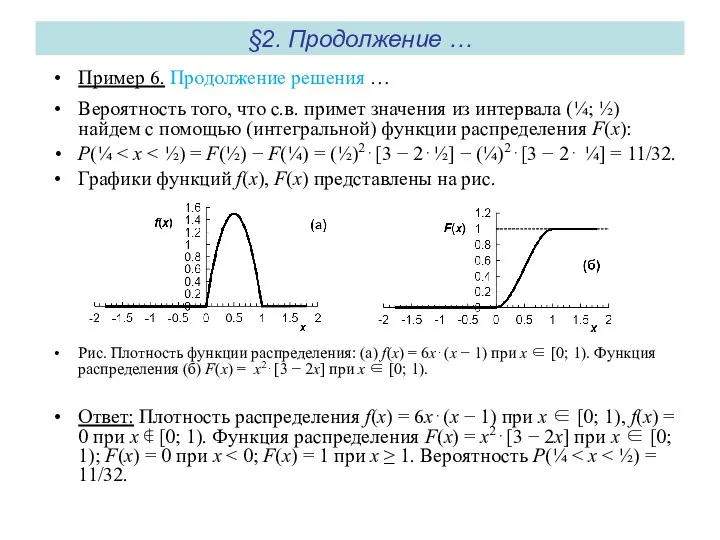
§2. Продолжение … Пример 6. Продолжение решения … Вероятность того, что

§2. Продолжение …

Пример 6. Продолжение решения …
Вероятность того, что с.в. примет

значения из интервала (¼; ½) найдем с помощью (интегральной) функции распределения F(x):
P(¼ < x < ½) = F(½) − F(¼) = (½)2⋅[3 − 2⋅½] − (¼)2⋅[3 − 2⋅ ¼] = 11/32.
Графики функций f(x), F(x) представлены на рис.
Рис. Плотность функции распределения: (а) f(x) = 6x⋅(x − 1) при x ∈ [0; 1). Функция распределения (б) F(x) = x2⋅[3 − 2x] при x ∈ [0; 1).
Ответ: Плотность распределения f(x) = 6x⋅(x − 1) при x ∈ [0; 1), f(x) = 0 при x ∉ [0; 1). Функция распределения F(x) = x2⋅[3 − 2x] при x ∈ [0; 1); F(x) = 0 при x < 0; F(x) = 1 при x ≥ 1. Вероятность P(¼ < x < ½) = 11/32.
Слайд 25

§2. Продолжение … Обобщим данные выше определения числовых характеристик распределения случайной

§2. Продолжение …

Обобщим данные выше определения числовых характеристик распределения случайной величины

на случай н.с.в.
Определение: Математическим ожиданием M(X) непрерывной случайной величины X, называют величину интеграла:
+∞
M(X) = ∫ x⋅f(x)dx.
−∞
Определение: Дисперсией D(X) н.с.в. X, называют величину:
+∞
D(X) = ∫ [x − M(X)]2⋅f(x)dx.
−∞
Определение: Средним квадратичным (стандартным) отклонением (СКО) σ(X) н.с.в. X, называют квадратный корень из дисперсии:
σ(X) = √D(X).
Замечание: Если фактическим диапазоном изменения ПФР f(X) является промежуток (a; b), т.е. f(x) отлично от тождественного нуля при x ∈ (a; b), то несобственные интегралы в пределах от −∞ до +∞ в определениях M(X) и D(X) могут быть заменены определенными интегралами в пределах от a до b.
Слайд 26

§2. Продолжение … Теорема (формула вычисления дисперсии н.с.в.). Дисперсия D(X) н.с.в.

§2. Продолжение …

Теорема (формула вычисления дисперсии н.с.в.). Дисперсия D(X) н.с.в. X

может быть найдена по формуле:
+∞
D(X) = ∫ x2⋅f(x)dx − M2(X) = M(X2) − M2(X),
−∞
где математическое ожидание
+∞
M(X) = ∫ x⋅f(x)dx.
−∞
Док-во: Доказательство утверждения осуществляется путем цепочки преобразований, следующих непосредственно из определения дисперсии н.с.в.:
+∞ +∞
D(X) = ∫ [x − M(X)]2⋅f(x)dx = ∫ [x2 − 2xM(X) + M2(X)]⋅f(x)dx =
−∞ −∞
+∞ +∞ +∞ +∞
= ∫ x2⋅f(x)dx − 2⋅M(X)⋅∫ x⋅f(x)dx + M2(X)⋅ ∫ f(x)dx = ∫ x2⋅f(x)dx − M2(X) =
−∞ −∞ −∞ −∞
= M(X2) − M2(X), ч.т.д.
Слайд 27

§2. Продолжение … Определение: Равномерным на промежутке (a; b) называется распределение

§2. Продолжение …

Определение: Равномерным на промежутке (a; b) называется распределение вероятностей,

заданное ПФР f(X) вида:
f(x) = С = Const при x ∈ (a; b), f(x) ≡ 0 при x ∉ (a; b).
Найдем числовые характеристики равномерно распределенной с.в. X.
− Нормировка:
+∞ b
∫ f(x)dx = ∫ Cdx = C⋅(b − a) = 1, откуда C = 1/(b − a).
−∞ a
− Математическое ожидание:
+∞ b
M(X) = ∫ x⋅f(x)dx = [1/(b−a)] ∫ xdx = ½ (b2 − a2)/(b − a) = ½ (b + a).
−∞ a
− Дисперсия:
+∞ b
D(X) = ∫ x2⋅f(x)dx − M2(X) = [1/(b−a)] ∫ x2dx − [½ (b + a)]2 =
−∞ a
= ⅓ (b3 − a3)/(b − a) − ¼ (b + a)2 =  (b − a)2.
− СКО: σ(X) = √D(X) = (b − a)/2√3.
Слайд 28

§2. Продолжение … Пример 7. Найти числовые характеристики н.с.в. X, равномерно

§2. Продолжение …

Пример 7. Найти числовые характеристики н.с.в. X, равномерно распределенной

в промежутке от a = 1 до b = 5.
Решение: Нормируем ПФР для равномерного на (1; 5) распределения:
5
∫ Cdx = C⋅(5 − 1) = 4C = 1, откуда C = ¼.
1
Так что ПФР f(x) = ¼ при x ∈ (1; 5) и f(x) ≡ 0 при x ∉ (1; 5) (см. рис.).
Функция распределения F(X) равна F(x) = ¼⋅(x − 1) при x ∈ (1; 5).
5
Математическое ожидание: M(X) = ¼ ∫ xdx = ¼⋅½⋅(52 − 12) = 3.
1
5
Дисперсия: D(X) = ¼ ∫ x2dx − M2(X) = ¼⋅⅓⋅(53 − 13) − 3 = 7.
1
СКО: σ(X) = √D(X) = √22/3 ≈ 2,708.
Слайд 29

§2. … продолжение Историческая справка: Иоганн Карл Фри́дрих Га́усс (нем. Johann

§2. … продолжение

Историческая справка:
Иоганн Карл Фри́дрих Га́усс
(нем. Johann Carl Friedrich Gauß;

30 апреля 1777,
Брауншвейг − 23 февраля 1855 г., Геттинген −
Немецкий математик, астроном и физик,
считается одним из величайших математиков
всех времён, «королём математиков».
Дед Гаусса был бедным крестьянином, отец — садовником,
каменщиком, смотрителем каналов в герцогстве Брауншвейг. Уже в
двухлетнем возрасте мальчик показал себя вундеркиндом. В три года
он умел читать и писать, даже исправлял счётные ошибки отца. Согласно
легенде, школьный учитель математики, чтобы занять детей на долгое
время, предложил им сосчитать сумму чисел от 1 до 100. Юный Гаусс
заметил, что попарные суммы с противоположных концов одинаковы:
1+100=101, 2+99=101 и т. д., и мгновенно получил результат 101 × 50 = 5050. До самой старости он привык большую часть вычислений производить в уме.
С учителем ему повезло: М. Бартельс (впоследствии учитель Лобачевского) оценил исключительный талант юного Гаусса и сумел выхлопотать ему стипендию от герцога Брауншвейгского. Это помогло Гауссу закончить колледж Collegium Carolinum в Брауншвейге (1792—1795).
Слайд 30

§2. … продолжение Историческая справка: Карл Гаусс (продолжение) Свободно владея множеством

§2. … продолжение

Историческая справка: Карл Гаусс (продолжение)
Свободно владея множеством языков, Гаусс

некоторое время колебался в выборе между филологией и математикой, но предпочёл последнюю. Он очень любил латинский язык и значительную часть своих трудов написал на латыни; любил английскую, французскую и русскую литературу. В возрасте 62 лет Гаусс начал изучать русский язык, чтобы ознакомиться с трудами Лобачевского, и вполне преуспел в этом деле.
В колледже Гаусс изучил труды Ньютона, Эйлера, Лагранжа. Уже там он сделал несколько открытий в теории чисел, в том числе доказал закон взаимности квадратичных вычетов. Лежандр, правда, открыл этот важнейший закон раньше, но строго доказать не сумел; Эйлеру это также не удалось. Кроме этого, Гаусс создал «метод наименьших квадратов» (тоже независимо открытый Лежандром) и начал исследования в области «нормального распределения ошибок».
С 1795 по 1798 год Гаусс учился в Гёттингенском университете. Это наиболее плодотворный период в жизни Гаусса.
1796 год: Гаусс доказал возможность построения с помощью циркуля и линейки правильного семнадцатиугольника. Более того, он разрешил проблему построения правильных многоугольников до конца и нашёл критерий возможности построения правильного n-угольника с помощью циркуля и линейки: если n — простое число, то оно должно быть вида 22k + 1 (числом Ферма). Этим открытием Гаусс очень дорожил и завещал изобразить на его могиле правильный 17-угольник, вписанный в круг.
С 1796 года Гаусс ведёт краткий дневник своих открытий. Многое он, подобно Ньютону, не публиковал, хотя это были результаты исключительной важности (эллиптические функции, неевклидова геометрия и др.). Своим друзьям он пояснял, что публикует только те результаты, которыми доволен и считает завершёнными. Многие отложенные или заброшенные им идеи позже воскресли в трудах Абеля, Якоби, Коши, Лобачевского и др. Кватернионы он тоже открыл за 30 лет до Гамильтона (назвав их «мутациями»).
Все многочисленные опубликованные труды Гаусса содержат значительные результаты, сырых и проходных работ не было ни одной.
Слайд 31

§2. … продолжение Историческая справка: Карл Гаусс (продолжение) 1798 год: закончен

§2. … продолжение

Историческая справка: Карл Гаусс (продолжение)
1798 год: закончен шедевр «Арифметические

исследования» (лат. Disquisitiones Arithmeticae), напечатана только в 1801 году.
В этом труде подробно излагается теория сравнений в современных (введенных им) обозначениях, решаются сравнения произвольного порядка, глубоко исследуются квадратичные формы, комплексные корни из единицы используются для построения правильных n-угольников, изложены свойства квадратичных вычетов, приведено его доказательство квадратичного закона взаимности и т. д. Гаусс любил говорить, что математика — царица наук, а теория чисел — царица математики.
1798—1816 годы
В 1798 году Гаусс вернулся в Брауншвейг и жил там до 1807 года. Герцог продолжал опекать молодого гения. Он оплатил печать его докторской диссертации (1799) и пожаловал неплохую стипендию. В своей докторской Гаусс впервые доказал основную теорему алгебры. До Гаусса было много попыток это доказать, наиболее близко к цели подошёл Д'Аламбер. Гаусс неоднократно возвращался к этой теореме и дал 4 различных доказательства её.
С 1799 года Гаусс — приват-доцент Брауншвейгского университета.
1801 год: избирается членом-корреспондентом Петербургской Академии наук.
После 1801 года Гаусс, не порывая с теорией чисел, расширил круг своих интересов, включив в него и естественные науки. Катализатором послужило открытие малой планеты Церера (1801), вскоре после наблюдений потерянной. 24-летний Гаусс проделал (за несколько часов) сложнейшие вычисления по новому, открытому им же методу, и указал место, где искать беглянку; там она, к общему восторгу, и была вскоре обнаружена.
Слава Гаусса становится общеевропейской. Многие научные общества Европы избирают Гаусса своим членом, герцог увеличивает пособие, а интерес Гаусса к астрономии ещё более возрастает.
.
Слайд 32

§2. … продолжение Историческая справка: Карл Гаусс (продолжение) 1805 год: Гаусс

§2. … продолжение

Историческая справка: Карл Гаусс (продолжение)
1805 год: Гаусс женился на

Иоганне Остгоф. У них было трое детей.
1806 год: от раны, полученной на войне с Наполеоном, умирает его великодушный покровитель-герцог. Несколько стран наперебой приглашают Гаусса на службу (в том числе в Петербург). По рекомендации Александра фон Гумбольдта Гаусса назначают профессором в Гёттингене и директором Гёттингенской обсерватории. Эту должность он занимал до самой смерти.
1807 год: наполеоновские войска занимают Гёттинген. Все граждане облагаются контрибуцией, в том числе огромную сумму — 2000 франков — требуется заплатить Гауссу. Ольберс и Лаплас тут же приходят ему на помощь, но Гаусс отклонил их деньги; тогда неизвестный из Франкфурта прислал ему 1000 гульденов, и этот дар пришлось принять. Только много позднее узнали, что неизвестным был курфюрст Майнцский, друг Гёте.
1809 год: новый шедевр, «Теория движения небесных тел». Изложена каноническая теория учёта возмущений орбит. Как раз в четвёртую годовщину свадьбы умирает Иоганна, вскоре после рождения третьего ребёнка. В Германии разруха и анархия. Это самые тяжёлые годы для Гаусса.
1810 год: новая женитьба, на Минне Вальдек, подруге Иоганны. Число детей Гаусса вскоре увеличивается до шести.
1810 год: новые почести. Гаусс получает премию Парижской академии наук и золотую медаль Лондонского королевского общества.
1811 год: появляется новая комета. Гаусс быстро и очень точно рассчитывает её орбиту. Начинает работу над комплексным анализом, открывает (но не публикует) теорему, позже переоткрытую Коши и Вейерштрассом: интеграл от аналитической функции по замкнутому контуру равен нулю.
1812 год: исследование гипергеометрического ряда, обобщающего разложение практически всех известных тогда функций. Знаменитую комету «пожара Москвы» (1812) всюду наблюдают, пользуясь вычислениями Гаусса.
1815 год: публикует первое строгое доказательство основной теоремы алгебры.
.
.
Слайд 33

§2. … продолжение Историческая справка: Карл Гаусс (продолжение) 1816—1855 годы1821 год:

§2. … продолжение

Историческая справка: Карл Гаусс (продолжение)
1816—1855 годы1821 год: в связи

с работами по геодезии Гаусс начинает исторический цикл работ по теории поверхностей. В науку входит «гауссова кривизна». Положено начало дифференциальной геометрии. Именно результаты Гаусса вдохновили Римана на его классическую диссертацию о «римановой геометрии».
Итогом изысканий Гаусса была работа «Исследования относительно кривых поверхностей» (1822). В ней свободно используются общие криволинейные координаты на поверхности. Гаусс далеко развил метод конформного отображения, которое в картографии сохраняет углы (но искажает расстояния); оно применяется также в аэро/гидродинамике и электростатике.
1824 год: избирается иностранным членом Петербургской Академии наук.
Гаусс в 1828 г.1825 год: открывает гауссовы комплексные целые числа, строит для них теорию делимости и сравнений. Успешно применяет их для решения сравнений высоких степеней.
Гаусс и Вебер. Скульптура в Гёттингене.1831 год: умирает вторая жена, у Гаусса начинается тяжелейшая бессонница. В Геттинген приезжает приглашённый по инициативе Гаусса 27-летний талантливый физик Вильгельм Вебер, с которым Гаусс познакомился в 1828 году, в гостях у Гумбольдта. Оба энтузиаста науки сдружились, несмотря на разницу в возрасте, и начинают цикл исследований электромагнетизма.
1832 год: «Теория биквадратичных вычетов». С помощью тех же целых комплексных гауссовых чисел доказываются важные арифметические теоремы не только для комплексных, но и для вещественных чисел. Здесь же он приводит геометрическую интерпретацию комплексных чисел, которая с этого момента становится общепринятой.
1833 год: Гаусс изобретает электрический телеграф и (вместе с Вебером) строит его действующую модель.
1837 год: Вебера увольняют за отказ принести присягу новому королю Ганновера. Гаусс вновь остался в одиночестве.
Слайд 34

§2. … продолжение Историческая справка: Карл Гаусс (продолжение) 1839 год: 62-летний

§2. … продолжение

Историческая справка: Карл Гаусс (продолжение)
1839 год: 62-летний Гаусс овладевает

русским языком и в письмах в Петербургскую Академию просил прислать ему русские журналы и книги, в частности «Капитанскую дочку» Пушкина. Предполагают, что это связано с работами Лобачевского. В 1842 году по рекомендации Гаусса Лобачевский избирается иностранным членом-корреспондентом Гёттингенского королевского общества.
Умер Гаусс 23 февраля 1855 года в Гёттингене.
Современники вспоминают Гаусса как жизнерадостного, дружелюбного человека, с отличным чувством юмора.
- Предыдущая
Классическое определение вероятности. Геометрическая вероятность.
Следующая -
Подходы к определению понятия умственная отсталость

Похожие презентации

Презентация "Природа и архитектура" - скачать презентации по МХК
Педагогические технологии личностно- ориентированного и развивающего обучения
Стилевое многообразие культуры XVII-XVII вв
Огнестойкость СК.ppt
Икона Казанской Божьей Матери
История физики 2
Карнавал. Урок изобразительного искусства 7 класс
Сказка о мертвой царевне и семи богатырях - часть 1 - презентация для начальной школы
Россия в XVII веке: от Смуты к утверждению самодержавно-крепостнического строя
Виды прерываний и методы обработки современных компьютерах
Гирдромеханические передачи
Сечения и разрезы
Презентация Гегель Абсолютный идеализм
Привлечение клиентов в салон красоты через Интернет
Туризм в России
Система мероприятий по финансированию инновационной деятельности организации ООО Автоцент «Тройка»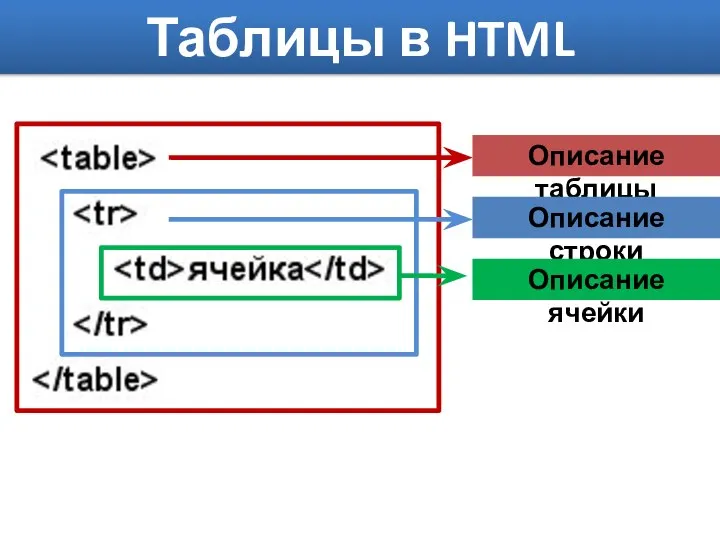
Таблицы в HTML
Объекты гос. регистрации прав на недвижимое имущество и сделок с ним
Национальные деловые культуры
Тип стрекающие
Viera Plasma Display PC Board Recycling. Component Level Repair. Troubleshooting Hints / Common Symptoms
Образование и наука в первой половине XIX века
Либерализм и его принципы. Формирование либерализма
Методика расследования экологических преступлений
ИЗМЕНЕНИЯ В НАЛОГОВОМ ЗАКОНОДАТЕЛЬСТВЕ для физических лиц - Новые стратегии торговли - Примеры сальдирования налогов - Краткое о
Железы внутренней секреции
Интернетэкзамен в сфере профессионального образования (ФЭПО)
Нуклеофильное замещение у насыщенного атома углерода
Вы можете прислать нам Вашу презентацию и мы опубликуем ее на сайте.
Обратная связь
Для правообладателей
Email: Нажмите что бы посмотреть