Содержание
- 2. Учебный вопрос №1 Равномерное распределение НСВ
- 3. Рассмотрим непрерывную случайную величину Х, возможные значения которой лежат в некотором интервале и равновероятны. Плотность вероятности
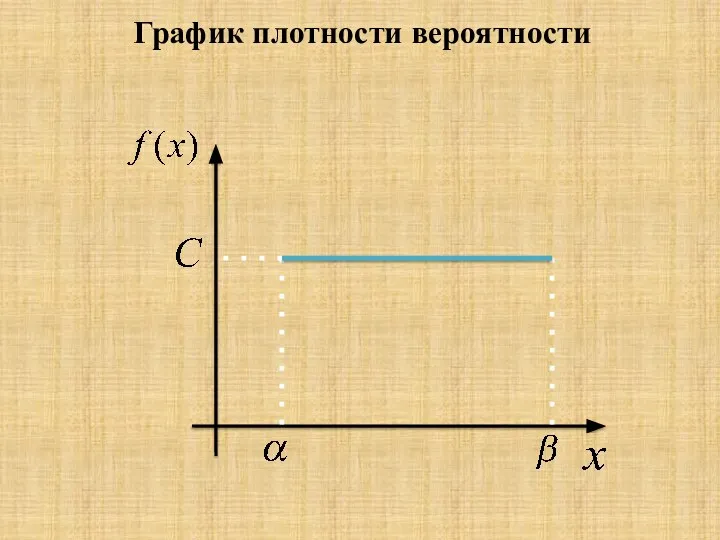
- 4. График плотности вероятности
- 5. Выразим параметр С через α и β. Для этого используем тот факт, что интеграл от плотности
- 6. Плотность вероятности равномерно распределенной случайной величины
- 7. Найдем функцию распределения:
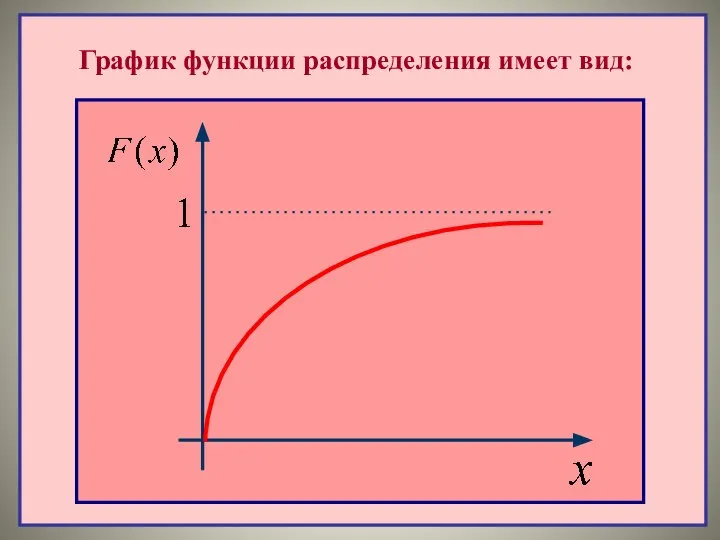
- 8. Функция распределения равномерно распределенной случайной величины
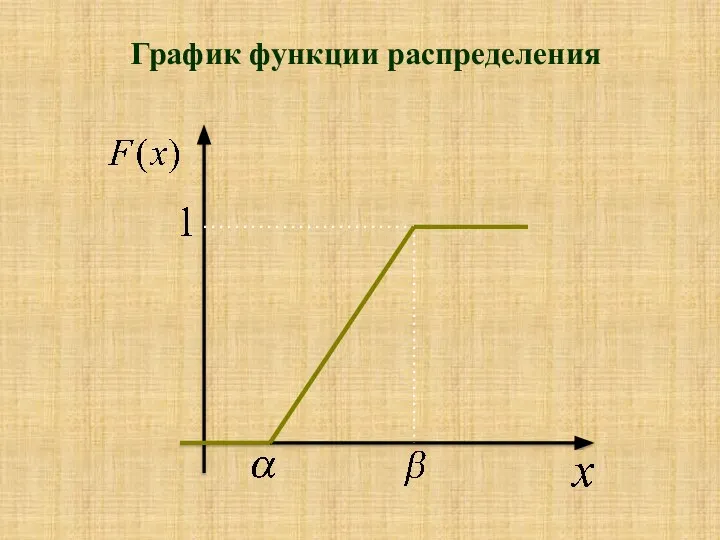
- 9. График функции распределения
- 10. Вычислим математическое ожидание и дисперсию случайной величины, подчиняющейся равномерному распределению.
- 12. Тогда среднеквадратичное отклонение будет иметь вид:
- 13. Пусть случайная величина Х равномерно распределена на участке [0;100]. Найти вероятности: Р(0 P(-10 Пример 3
- 14. Для нахождения искомых вероятностей используем формулу: Где F(α) и F(β) - функция распределения на концах рассматриваемого
- 16. Учебный вопрос №2 Нормальное распределение НСВ
- 17. Нормальный (гауссов) закон распределения Непрерывная случайная величина Х называется распределенной по нормальному закону с параметрами a,
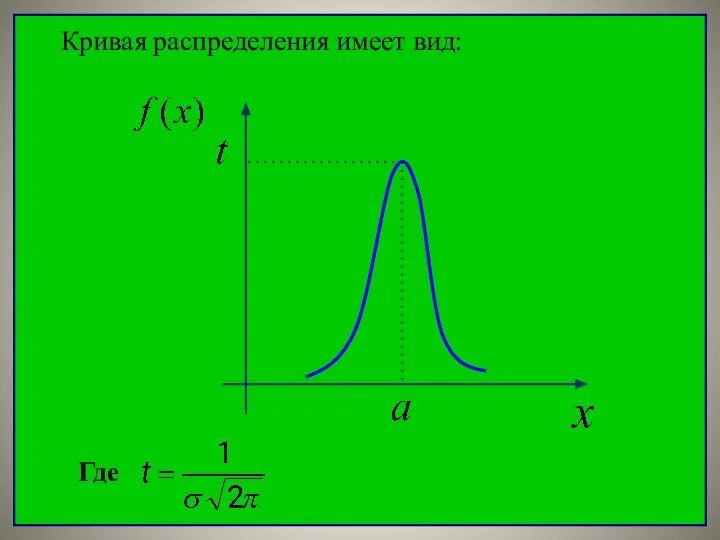
- 18. Кривая распределения имеет вид: Где
- 19. Выясним смысл параметров распределения Гаусса. Для этого вычислим характеристики этого распределения (математическое ожидание и дисперсию). Делаем
- 20. Разбиваем на сумму двух интегралов: Второй интеграл представляет собой интеграл Пуассона:
- 21. В первом интеграле вносим t под знак дифференциала: Таким образом, параметр a представляет собой математическое ожидание
- 22. Этот интеграл берем по частям:
- 23. Первое слагаемое в скобках равно 0, так как экспонента в минус бесконечной степени будет стремиться к
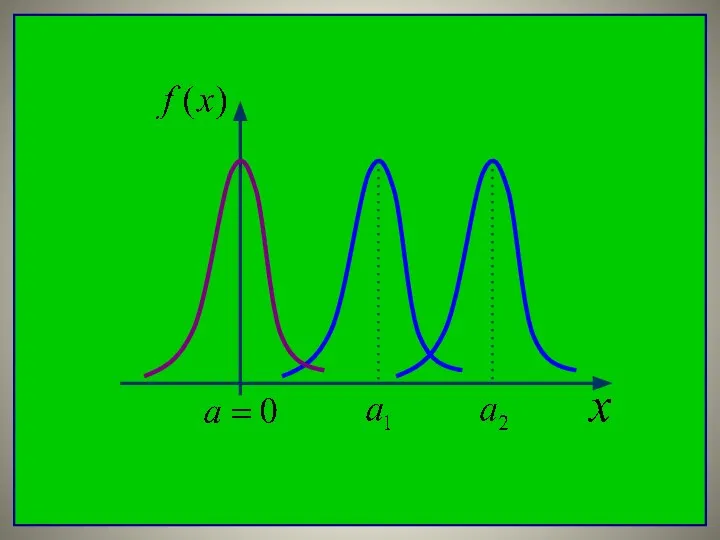
- 24. Если изменять параметр a , кривая распределения будет смещаться вдоль оси абсцисс, не изменяя при этом
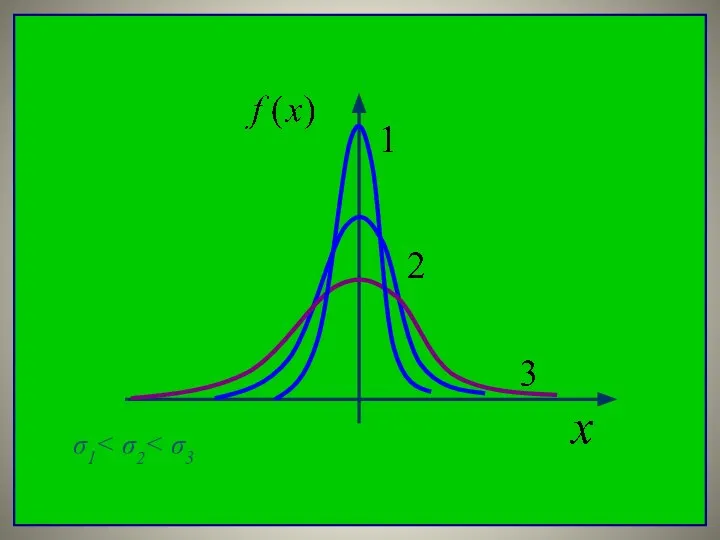
- 26. Параметр σ характеризует не положение, а саму форму кривой распределения. При его увеличении кривая распределения становится
- 27. σ1
- 28. То, что случайная величина Х распределена по нормальному закону с параметрами a, σ>0 , обозначается При
- 29. Найдем функцию распределения случайной величины Х . Сделаем замену переменной:
- 30. Последний интеграл не выражается через элементарные функции, но его можно вычислить через специальную функцию (так называемый
- 31. Функция Ф*(х) называется нормальной функцией распределения. Ее значения приведены в таблицах. Но большее распространение имеет функция
- 32. ВЕРОЯТНОСТЬ ПОПАДАНИЯ СВ НА ЗАДАННЫЙ УЧАСТОК
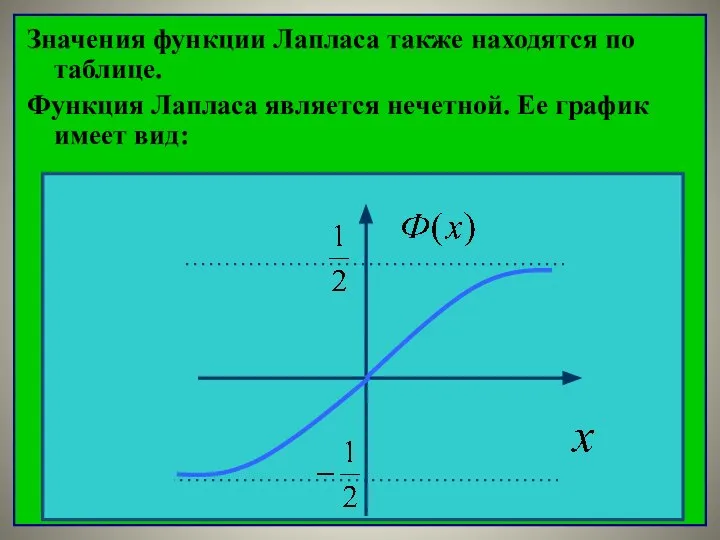
- 33. Значения функции Лапласа также находятся по таблице. Функция Лапласа является нечетной. Ее график имеет вид:
- 34. Пусть Х - нормально распределенная случайная величина с параметрами a, σ. Тогда ПРАВИЛО ТРЕХ СИГМ
- 35. Действительно,
- 36. Пусть случайная величина Х - рост наугад выбранного студента подчиняется нормальному распределению с параметром a=174 см.
- 37. Сначала определим параметр σ. Используем правило «3 сигм». Параметр a=174 см определяет средний рост студентов. Причем
- 40. Учебный вопрос №3 Показателное распределение НСВ
- 41. Пусть непрерывная случайная величина Х задана функцией распределения Показательное распределение ФУНКЦИЯ РАСПРЕДЕЛЕНИЯ СВ, РАСПРЕДЕЛЕННОЙ ПО ПОКАЗАТЕЛЬНОМУ
- 42. График функции распределения имеет вид:
- 43. Найдем плотность вероятности этой случайной величины. Плотность вероятности находится как производная от функции распределения: ПЛОТНОСТЬ ВЕРОЯТНОСТИ
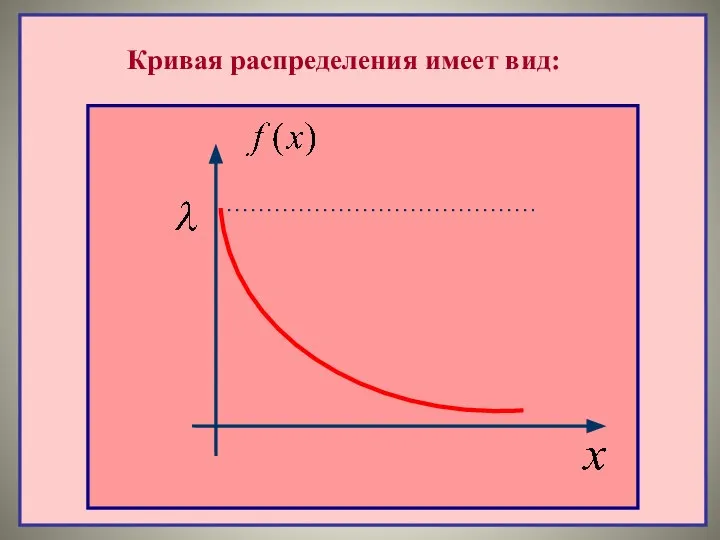
- 44. Кривая распределения имеет вид:
- 45. Найдем математическое ожидание и дисперсию случайной величины, распределенной по показательному закону. Вынесем константы за знак интеграла
- 46. Полученный определенный интеграл будем брать по частям:
- 47. Первые два слагаемых в пределе равны 0, т.к. экспонента в минус бесконечной степени стремиться к 0.
- 48. Как и в предыдущем случае, переходим к пределу определенного интеграла: Берем интеграл по частям:
- 49. Полученный интеграл еще раз берем по частям: Полученный интеграл табличный:
- 51. Скачать презентацию







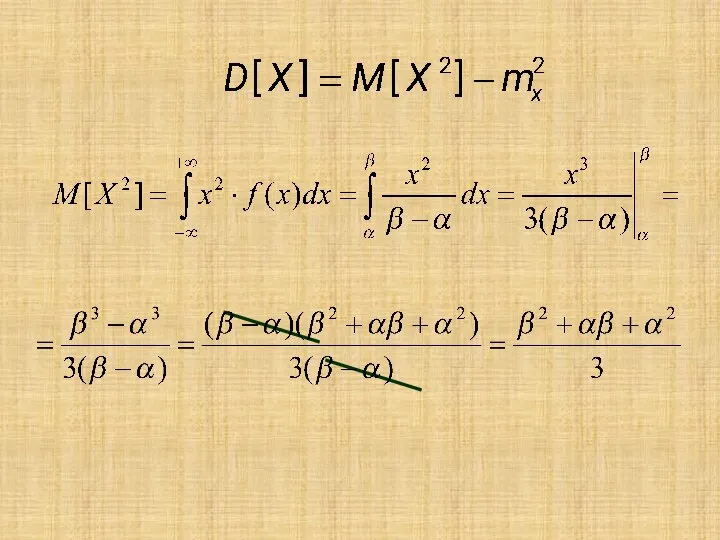

![Пусть случайная величина Х равномерно распределена на участке [0;100]. Найти вероятности: Р(0 P(-10 Пример 3](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/1306468/slide-12.jpg)




















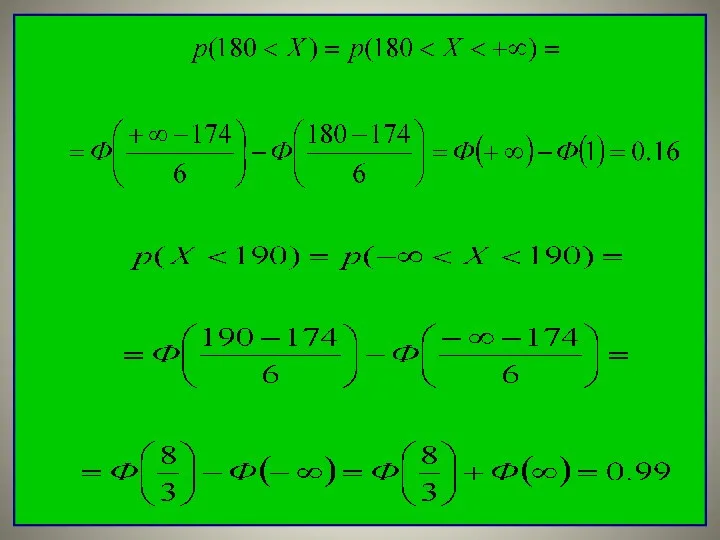









 Построение изображения в микроскопе, определение увеличения микроскопа
Построение изображения в микроскопе, определение увеличения микроскопа Шестакова Виктория ученица 3 класса «Б» НОУ «Школа- интернат № 8 ОАО «РЖД
Шестакова Виктория ученица 3 класса «Б» НОУ «Школа- интернат № 8 ОАО «РЖД Франция. Голосование в Генеральной Ассамблее
Франция. Голосование в Генеральной Ассамблее Московский Городской Психолого-Педагогический Университет Факультет «Психологического Консультирования» Кафедра «Индивидуаль
Московский Городской Психолого-Педагогический Университет Факультет «Психологического Консультирования» Кафедра «Индивидуаль Игра - викторина
Игра - викторина сарманова
сарманова Герой Российской Федерации сержант Янина Ирина Юрьевна
Герой Российской Федерации сержант Янина Ирина Юрьевна Уравнение х2 = а 8 класс
Уравнение х2 = а 8 класс Клеедощатые балки
Клеедощатые балки Дымковская игрушка
Дымковская игрушка Соединение с натягом. Характерные посадки и характеристики эксплуатационных свойств. Способы сборки
Соединение с натягом. Характерные посадки и характеристики эксплуатационных свойств. Способы сборки Криптографические методы и средства для защиты информации
Криптографические методы и средства для защиты информации Презентация Великий Шелковый Путь Историческое и культурное наследие казахстанского участка Великого шёлкового пути – фактор
Презентация Великий Шелковый Путь Историческое и культурное наследие казахстанского участка Великого шёлкового пути – фактор  Афиша значимых мероприятий МБУ «Управление культуры и организации досуга населения» на летний период 2018 года
Афиша значимых мероприятий МБУ «Управление культуры и организации досуга населения» на летний период 2018 года Медико-социальное значение ХНИБ
Медико-социальное значение ХНИБ ИНФОРМАЦИОННАЯ БЕЗОПАСНОСТЬ
ИНФОРМАЦИОННАЯ БЕЗОПАСНОСТЬ Гражданское общество и государство. Роль СМИ в политической жизни
Гражданское общество и государство. Роль СМИ в политической жизни “ҚАЗФОСФАТ” ЖШС
“ҚАЗФОСФАТ” ЖШС УРОВНИ~1.PPT
УРОВНИ~1.PPT Восстановление церквей
Восстановление церквей Т15 Р і РЕБ.ppt
Т15 Р і РЕБ.ppt Урок изобразительного искусства - презентация для начальной школы
Урок изобразительного искусства - презентация для начальной школы Патогенетические основы терапии заболеваний желудочно-кишечного тракта
Патогенетические основы терапии заболеваний желудочно-кишечного тракта , Щ об знайти суму або різницю дробів з різними знаменниками,треба спочатку звести їх до спільного знаменника. А далі – додавати аб
, Щ об знайти суму або різницю дробів з різними знаменниками,треба спочатку звести їх до спільного знаменника. А далі – додавати аб Довольствование или довольство. Библейское основание управления финансами
Довольствование или довольство. Библейское основание управления финансами Счета бухгалтерского учета
Счета бухгалтерского учета Индикатор – сигнализатор ДП-64
Индикатор – сигнализатор ДП-64 Договор транспортной экспедиции
Договор транспортной экспедиции