Непрерывные случайные величины и их законы распределения

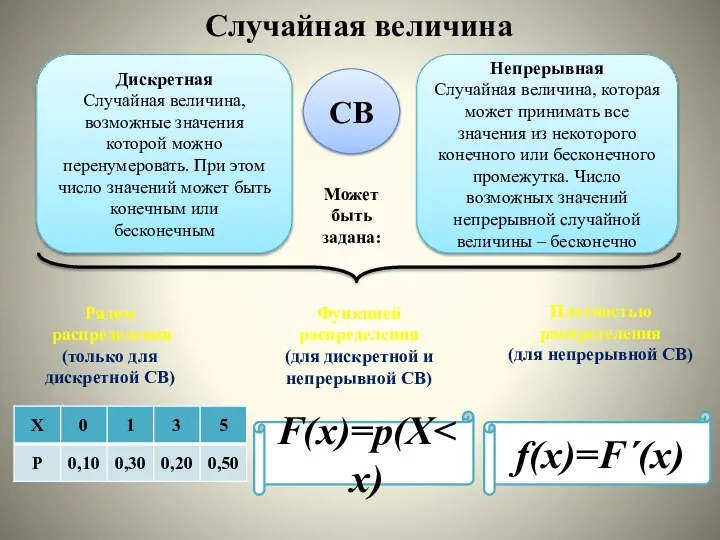
Случайная величина

Дискретная
Случайная величина, возможные значения которой можно перенумеровать. При этом число

Непрерывные случайные величины имеют бесконечное число возможных значений. Поэтому ввести для

Если СВ Х непрерывна, то вероятность того, что она примет конкретное

Рассмотрим непрерывную случайную величину Х с функцией распределения F(x).
Вычислим вероятность попадания

По определению производной этот предел равен производной функции F(x) :

=

Функция f(x),

Эта величина называется элементом вероятности и геометрически означает площадь элементарного прямоугольника

Выразим вероятность попадания на участок α до β через f(x). Вероятность

Отсюда можно выразить функцию распределения через плотность вероятности:

Плотность вероятности является
неотрицательной функцией
(т.к. функция распределения является
неубывающей функцией):

Свойства

Плотность вероятности является
непрерывной функцией.

Свойства плотности вероятности

2

Интеграл в бесконечных пределах
от плотности вероятности равен 1:

условие нормировки

3

Свойства плотности

Это свойство следует из того, что функция распределения на плюс бесконечности

Смысл математического ожидания и дисперсии остается таким же, как и в

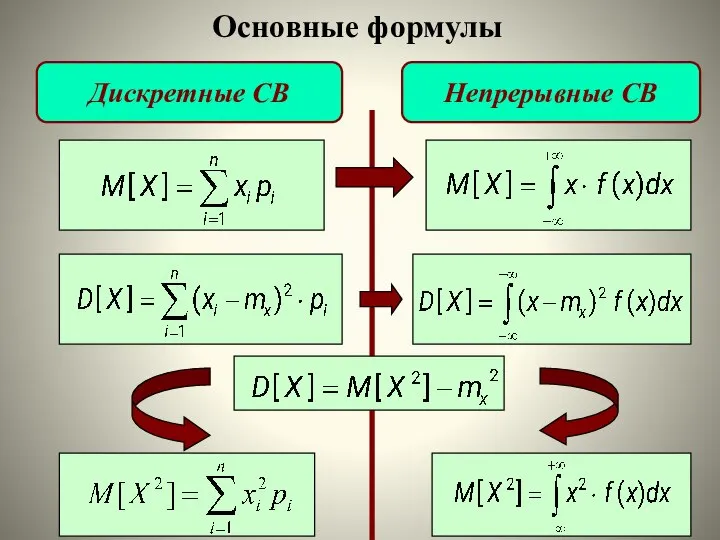
Дискретные СВ

Непрерывные СВ

Основные формулы

Функция распределения непрерывной
случайной величины задана выражением:

Найти величину a, плотность

1. Так как функция распределения F(x) непрерывна, то при х=1 ax2=1,

3. Вычисление вероятности попадания на заданный участок может быть произведено двумя

2 способ.
Используем формулу нахождения вероятности через плотность вероятности:

4. Находим математическое

5. Находим дисперсию:

Тогда

Случайная величина Х подчиняется
закону распределения

Найти величину a и функцию распределения.

Пример

2. Функция распределения находится путем интегрирования плотности вероятности:

1. Для нахождения

При 0

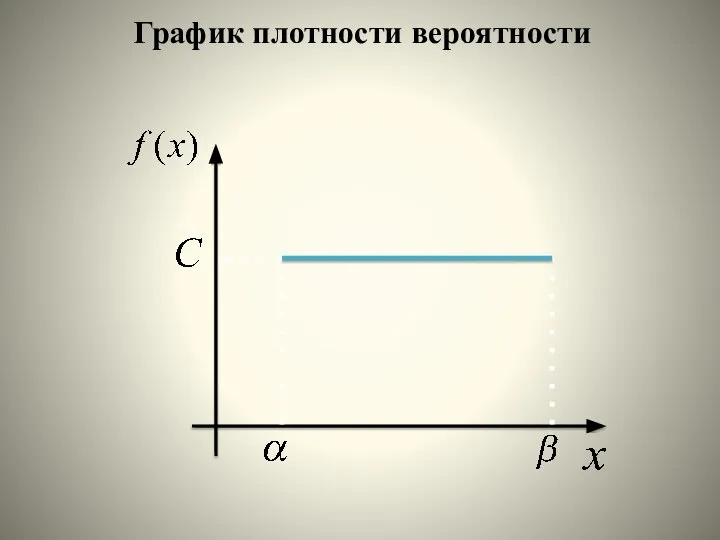
Рассмотрим непрерывную случайную величину Х, возможные значения которой лежат в некотором

График плотности вероятности

Выразим параметр С через α и β. Для этого используем тот

Плотность вероятности равномерно распределенной случайной величины

Найдем функцию распределения:

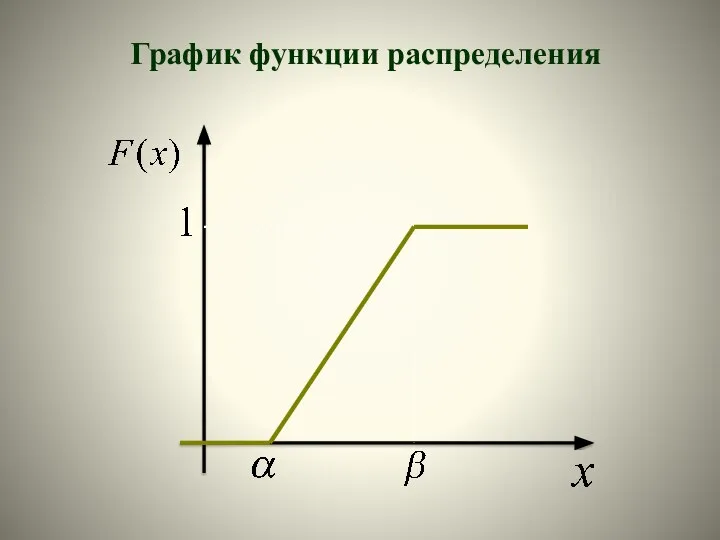
Функция распределения равномерно распределенной случайной величины

График функции распределения

Вычислим математическое ожидание и дисперсию
случайной величины, подчиняющейся равномерному распределению.

Тогда среднеквадратичное отклонение будет иметь вид:

Пусть случайная величина Х
равномерно распределена на
участке [0;100]. Найти вероятности:

Для нахождения искомых вероятностей используем формулу:

Где F(α) и F(β) - функция