Рекурсия. Метод решения задач

Определения

Рекурсивным называется объект, частично содержащий себя, или определенный с помощью самого

Рекурсивные определения

Натуральные числа:
0 – натуральное число
Если N – натуральное число, то

Рекурсивные определения

Факториал числа:
0!=1
N!=(N-1)!*N, для любого N>0;

Достоинство

Рекурсивное определение позволяет определить бесконечное множество объектов с помощью конечного высказывания

Рекурсия в программировании

С помощью конечной рекурсивной программы можно описать бесконечное вычисление,

Рекурсивные функции

Если некоторая подпрограмма (функция) содержит явную ссылку на саму себя,

Рекурсия

Рекурсия сводит решение задачи к решению более мелких идентичных задач
Сложные задачи

Факториал числа

Рекурсивное определение:
Fact(int n)
{ if(n==0) return 1;
else return (Fact(n-1));
}

Факториал числа: итеративное определение

long Factorial (int n)
{ int i;
long f;
if

Рекурсивное решение

При вызове подпрограммы всякий раз создаются новые экземпляры локальных переменных
При

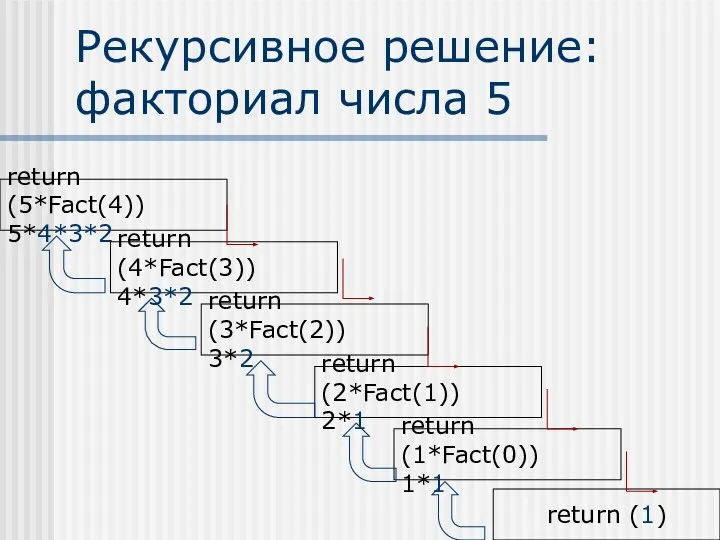
Рекурсивное решение: факториал числа 5

return (5*Fact(4))
5*4*3*2

return (4*Fact(3))
4*3*2

return (3*Fact(2))
3*2

return (2*Fact(1))
2*1

return (1*Fact(0))
1*1

return (1)

Свойства рекурсивного решения

Функция вызывает саму себя
При каждом вызове функции решается идентичная,

Ошибка в использовании рекурсии

Отсутствие базиса: void PRINT()
{ cout<<‘*’;
PRINT();
}
При вызове данной функции

Четыре вопроса о рекурсивном решении:

Как свести задачу к идентичным задачам меньшего

Числа Фибоначчи

F(n)=F(n-1)+F(n-2)
Необходимо 2 базиса:F(1)=1, F(2)=1;
int F(int n)
{ if (n<=2) return 1;

Задача о параде

Необходимо на параде расставить k оркестров и m платформ,

Задача о параде

Допустим, что у нас есть N оркестров и N

Задача о параде

Введем обозначения:
P(n)- количество вариантов организации парадов длиной n
F(n)-количество вариантов

Задача о параде
F(n)=P(n-1) – парад, завершающийся платформой длины n получается из

Задача о параде

Базис:
P(1)=2-парад длины один может состоять либо из платформы, либо

Дилемма мистера Спока

Сколько разных способов можно применить для исследования k планет,

Рассуждения мистера Спока

Есть две возможности:
Либо мы посещаем некоторую планету Х и

Получаем формулу:

c(n,k)=c(n-1,k-1)+ c(n-1,k), где
c(n-1,k-1) – количество групп, состоящих из k планет,

Базис:

c(k,k)=1 – можно выбрать только одну группу, состоящую из всех планет
c(n,0)=1

Разложение числа на слагаемые

Сколькими способами можно разбить число M на слагаемые
Обозначим

Разложение числа на слагаемые

Q(M,1)=1 – только одним способом можно представить число