Содержание
- 2. Реляционная алгебра Реляционная алгебра — это коллекция операций, которые принимают отношения в качестве операндов и возвращают
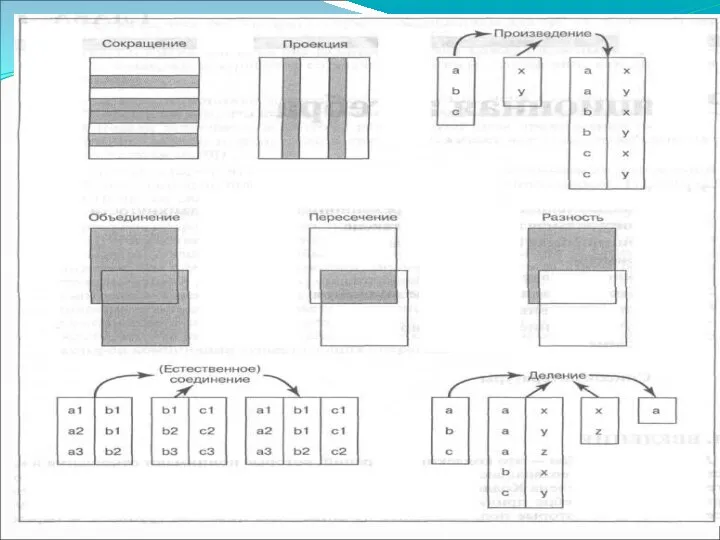
- 4. Реляционная алгебра Объединение В математике объединение двух множеств представляет собой множество всех элементов, принадлежащих либо к
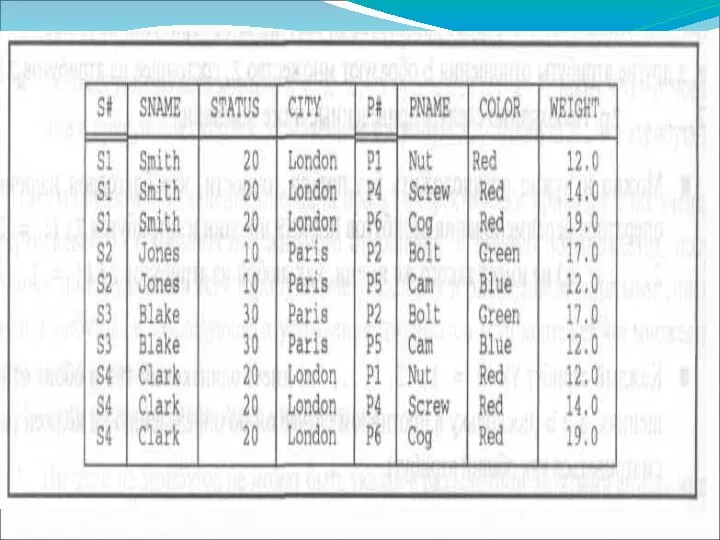
- 5. Примеры отношений Поставщики S { S#, SNAME, STATUS, CITY } PRIMARY KEY { S# } Поставки
- 6. Объединение отношений Но хотя этот результат можно назвать множеством, он не является отношением; отношения не могут
- 7. Объединение отношений Поэтому определение операции реляционного объединения должно быть таким: если даны отношения А и В
- 9. Объединение отношений Пример. Предположим, что отношения А и B имеют вид, показанный на рис. (оба они
- 10. Пересечение отношений Как и для объединения, и фактически по той же причине, для реляционной операции пересечения
- 11. Пересечение отношений Пример. Снова предположим, что отношения А и В показаны на рис. Тогда пересечение A
- 12. Разность отношений Как и для объединения и пересечения, для реляционной операции разности требуется, чтобы ее операнды
- 13. Разность отношений Пример. Снова предположим, что отношения А и В показаны на рис. Тогда результат операции
- 14. Произведение отношений В математике декартовым произведением (или сокращенно произведением) двух множеств является множество всех таких упорядоченных
- 15. Произведение отношений Поэтому реляционной версией декартова произведения служит расширенная форма этой операции, в которой каждая упорядоченная
- 16. Произведение отношений Итак, определим (реляционное) декартово произведение А TIMES В отношений А и В, не имеющих
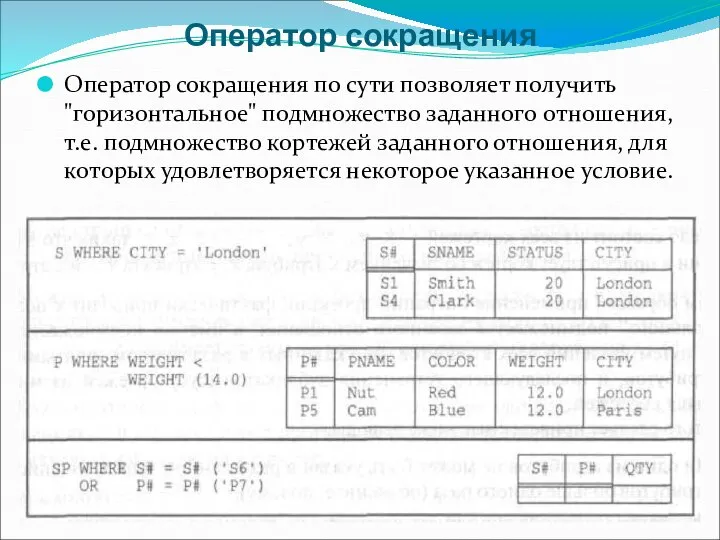
- 18. Оператор сокращения Оператор сокращения по сути позволяет получить "горизонтальное" подмножество заданного отношения, т.е. подмножество кортежей заданного
- 19. Операция проекции Предположим, что отношение А имеет атрибуты Х, Y, . . ., Z (и, возможно,
- 20. Операция проекции
- 21. Операция соединения Предположим, что отношения А и В, соответствен-но, имеют следующие атрибуты. X 1 , Х
- 22. Операция соединения Теперь множества { X I, Х 2, . . . , Xm },{ Yl,
- 24. Операция деления Предположим, что отношения А и В, соответственно, имеют следующие атрибуты: XI, Х2, . .
- 25. Операция деления Деление представляет собой отношение с заголовком {X} и телом, состоящим из всех кортежей {
- 26. Пример деления На рис. приведены некоторые примеры деления. В каждом случае делимое (DEND) представляет собой проекцию
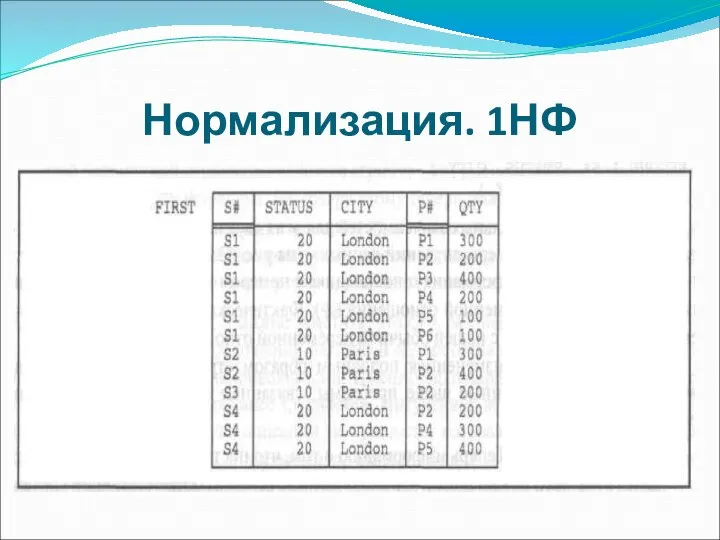
- 27. Нормализация. 1НФ
- 29. Скачать презентацию






















 Портрет Дорианa Грея
Портрет Дорианa Грея ПРАВОВЫЕ СЕМЬИ
ПРАВОВЫЕ СЕМЬИ ООО "Эдельвейс плюс"
ООО "Эдельвейс плюс" Всероссийский физкультурно-спортивный комплекс «Готов к труду и обороне» (ГТО) в Ростовской области
Всероссийский физкультурно-спортивный комплекс «Готов к труду и обороне» (ГТО) в Ростовской области Total Productivity Management (TPM), TQM, and Hoshin Kanri
Total Productivity Management (TPM), TQM, and Hoshin Kanri Европейски Социален Фонд 2007 – 2013 Оперативна програма Развитие на човешките ресурси BG051PO001-2.1.16 - Квалификационни услуги и обучения
Европейски Социален Фонд 2007 – 2013 Оперативна програма Развитие на човешките ресурси BG051PO001-2.1.16 - Квалификационни услуги и обучения  Презентация "Декоративное цветоводство" - скачать презентации по МХК
Презентация "Декоративное цветоводство" - скачать презентации по МХК Понятие психологии Гусайниев Гасан Т-114
Понятие психологии Гусайниев Гасан Т-114  Эксперимент в социальной психологии
Эксперимент в социальной психологии Методы нетарифного регулирования и меры, затрагивающие внешнюю торговлю товарами Выполнили студентки группы Э101 Овсянникова Над
Методы нетарифного регулирования и меры, затрагивающие внешнюю торговлю товарами Выполнили студентки группы Э101 Овсянникова Над Презентация Виды и характеристика торгово-политических режимов зарубежных государств или экономических союзов государств
Презентация Виды и характеристика торгово-политических режимов зарубежных государств или экономических союзов государств  Материнская (системная) плата
Материнская (системная) плата Банковская система в Германии
Банковская система в Германии  Жостовские подносы
Жостовские подносы ECON5
ECON5 Спортивный туризм на пешеходных дистанциях. Снаряжение для занятий спортивным туризмом
Спортивный туризм на пешеходных дистанциях. Снаряжение для занятий спортивным туризмом Милосердие, забота о слабых, взаимопомощь
Милосердие, забота о слабых, взаимопомощь Система MED-Мотроник
Система MED-Мотроник Каталог "Кухни"
Каталог "Кухни" Проектная работа "Русские бани"
Проектная работа "Русские бани"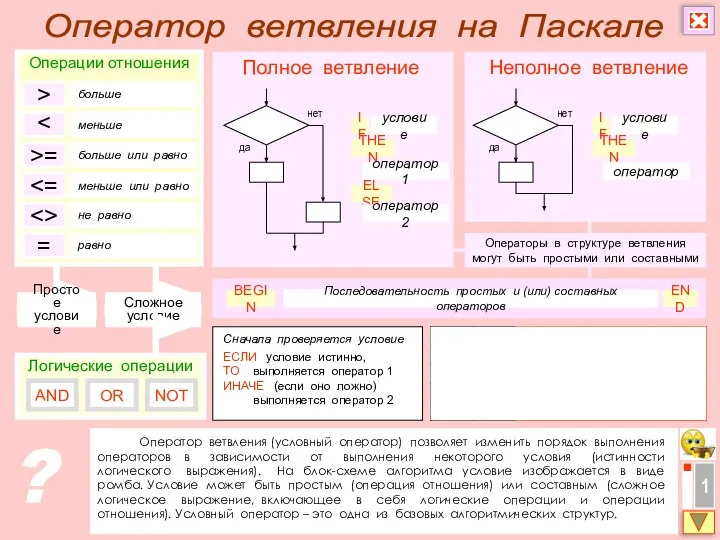 Оператор ветвления на Паскале
Оператор ветвления на Паскале Находится все, что продается. - презентация
Находится все, что продается. - презентация Аудит бизнес плана и порядок проведения
Аудит бизнес плана и порядок проведения  Проблема насилия в отношении детей: виды, формы, последствия, оценка факторов риска
Проблема насилия в отношении детей: виды, формы, последствия, оценка факторов риска Программа в среде Delphi (консольный режим)
Программа в среде Delphi (консольный режим) ИГРА «МОРСКОЙ БОЙ»
ИГРА «МОРСКОЙ БОЙ» Хеджирование рисков
Хеджирование рисков Модная «тусовка» Урок МХК 9 класс Учитель Коляда Наталья Ивановна
Модная «тусовка» Урок МХК 9 класс Учитель Коляда Наталья Ивановна