Содержание
- 2. Пример: Необходимо расположить все слова некоторого текста в алфавитном порядке Для решения данной задачи можно построить
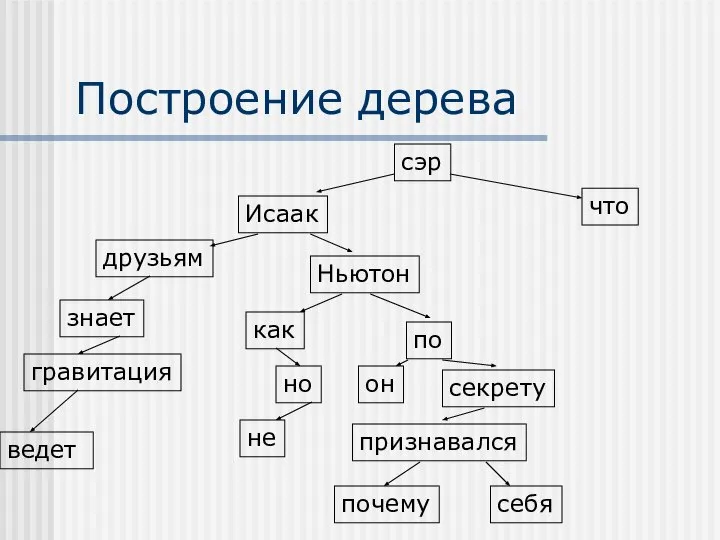
- 3. Допустим задан текст «Сэр Исаак Ньютон по секрету признавался друзьям, что он знает, как гравитация ведет
- 4. Текст в алфавитном порядке: ведет гравитация друзьям знает Исаак как не но Ньютон он по почему
- 5. Построение дерева сэр
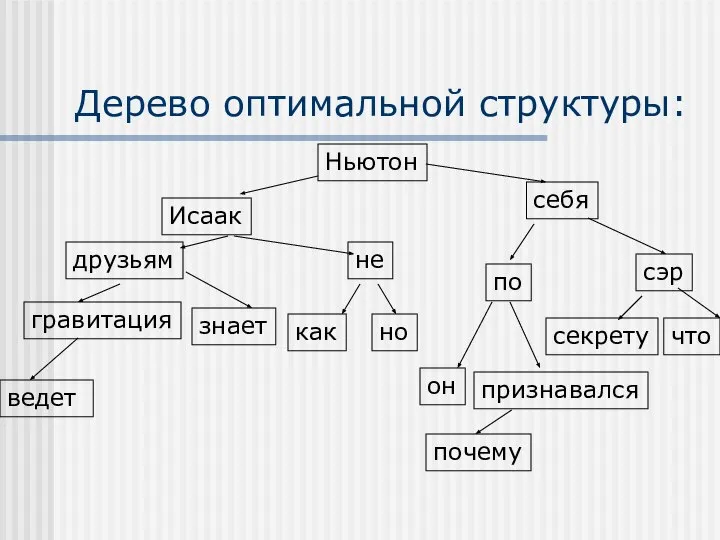
- 6. Дерево оптимальной структуры: Ньютон
- 7. Высота бинарного дерева Пусть бинарное дерево содержит элементы:10, 20, 30, 40, 50, 60, 70 Последовательная вставка
- 8. Дерево максимальной высоты
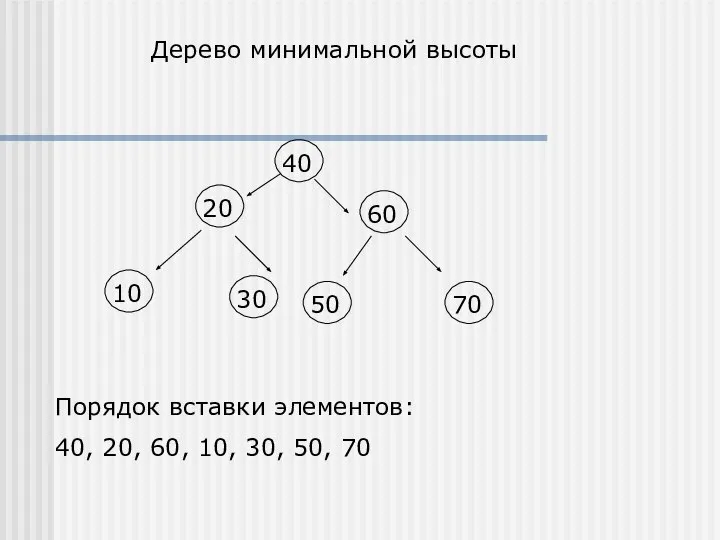
- 9. Дерево минимальной высоты Порядок вставки элементов: 40, 20, 60, 10, 30, 50, 70
- 10. Высота бинарного дерева Высота бинарного дерева зависит от порядка выполнения операций вставки и удаления элементов Высота
- 11. Цель: Создание деревьев, не теряющих баланса при выполнении операций вставки и удаления Эффективность поиска в таких
- 12. 2-3 дерево Каждый узел 2-3 дерева содержит одно или два значения Узлы дерева делятся на две
- 13. 2-3 дерево Принцип упорядоченности для 2-3 дерева: Для 2-узла – все значения, лежащие в левом поддереве,
- 14. Принцип упорядоченности для 2-3 дерева: Для 3-узла – упорядоченность означает следующее: Пусть А1 и А2– значения
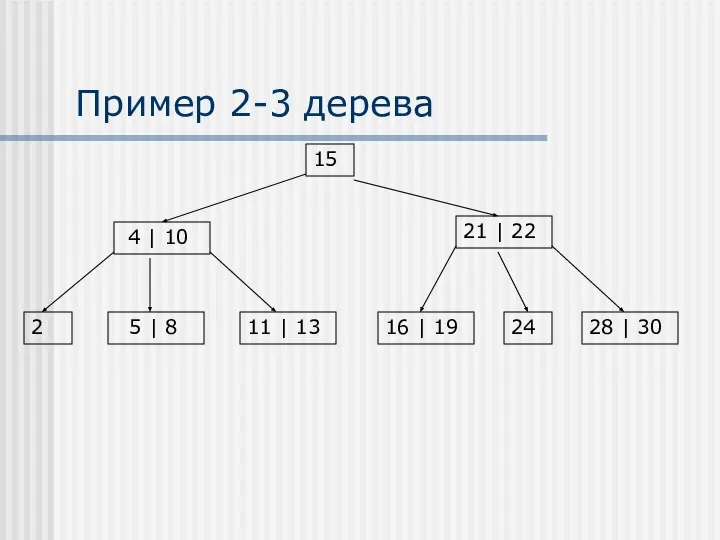
- 15. Пример 2-3 дерева 15 21 | 22 28 | 30 5 | 8 4 | 10
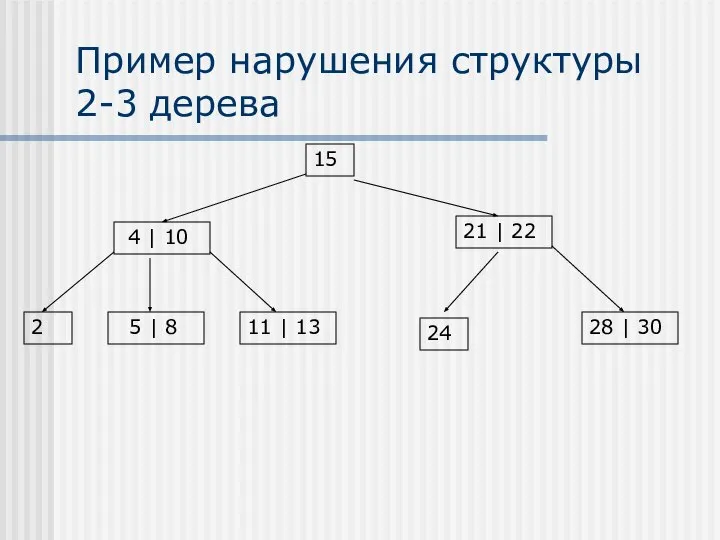
- 16. Пример нарушения структуры 2-3 дерева 15 21 | 22 28 | 30 5 | 8 4
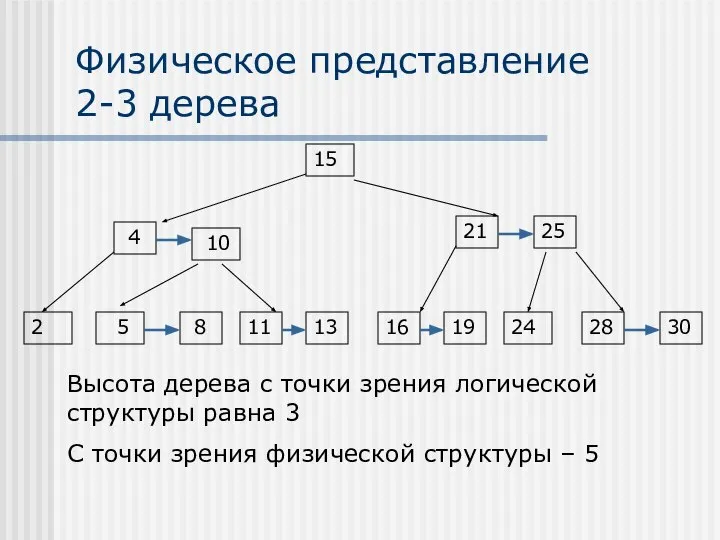
- 17. 2-3 дерево 2-3 дерево не является бинарным Все листья 2-3 дерева находятся на одном и том
- 18. Физическое представление 2-3 дерева 15 21 28 5 4 11 16 2 24 10 8 13
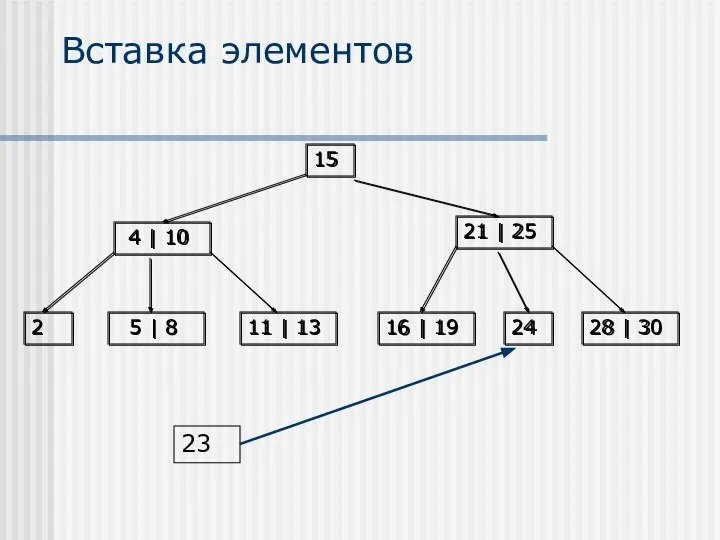
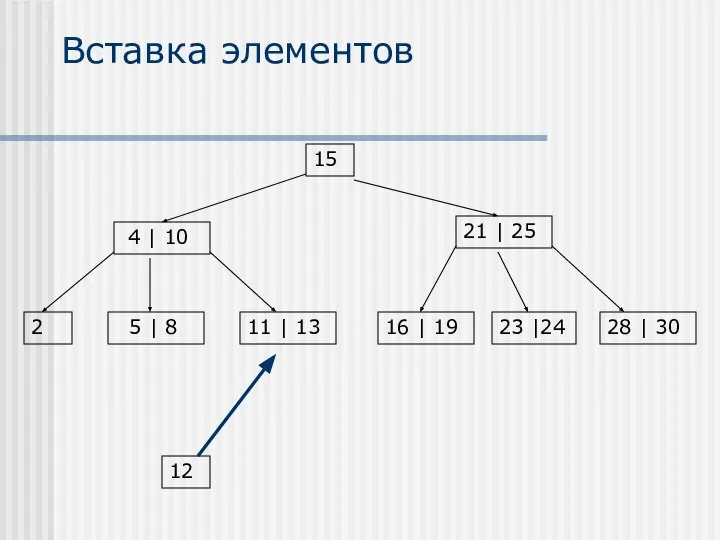
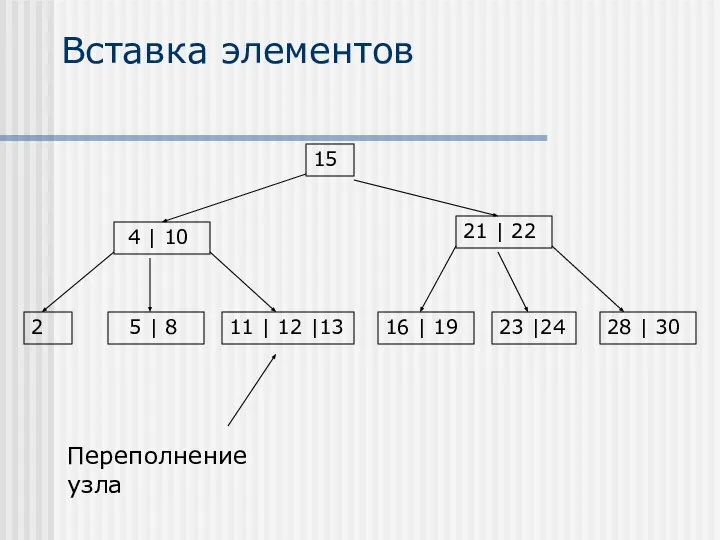
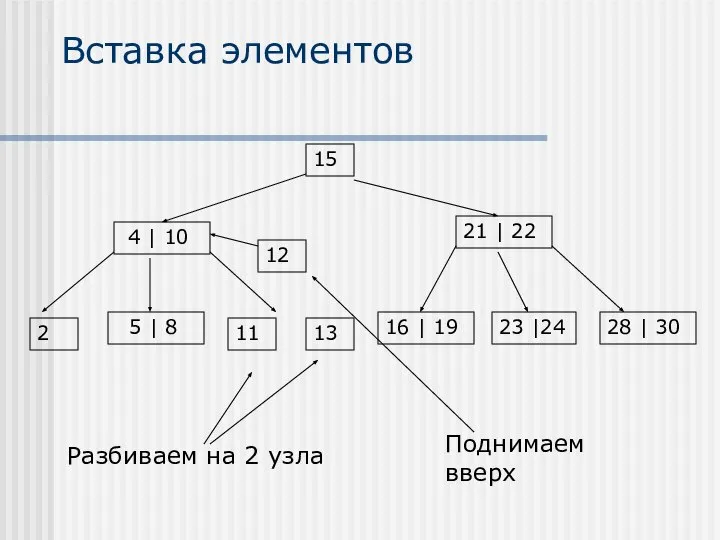
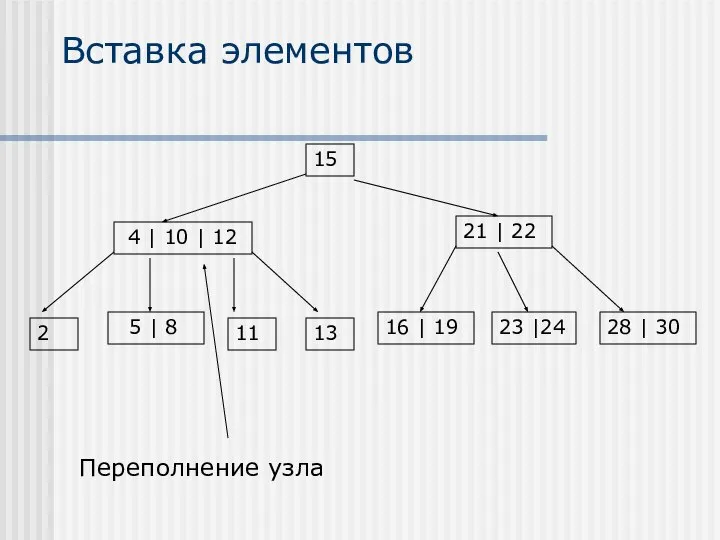
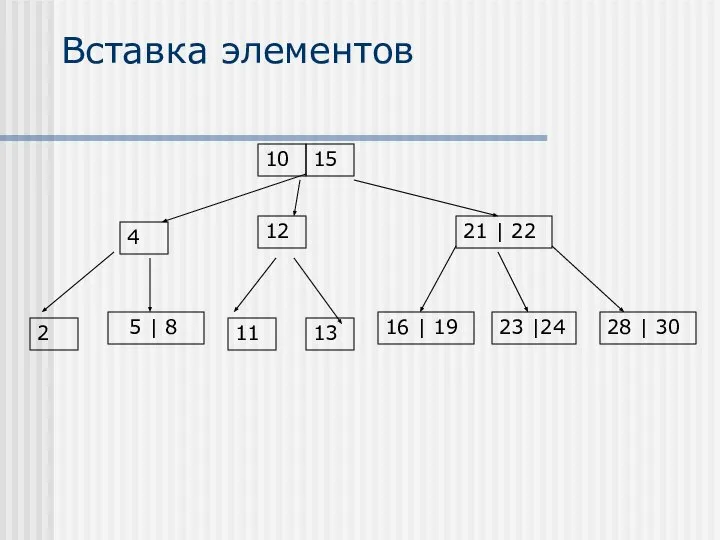
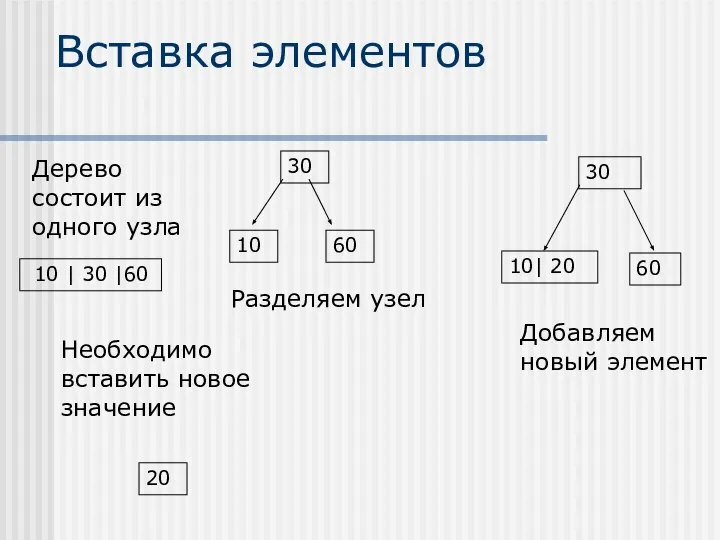
- 19. Вставка элементов Вставка элементов осуществляется только в листья В случае, если после вставки элемента образуется переполненный
- 20. Вставка элементов 23
- 21. Вставка элементов
- 22. Вставка элементов 12
- 23. Вставка элементов 15 21 | 22 28 | 30 5 | 8 4 | 10 11
- 24. Вставка элементов 15 21 | 22 28 | 30 5 | 8 4 | 10 16
- 25. Вставка элементов 15 21 | 22 28 | 30 5 | 8 4 | 10 |
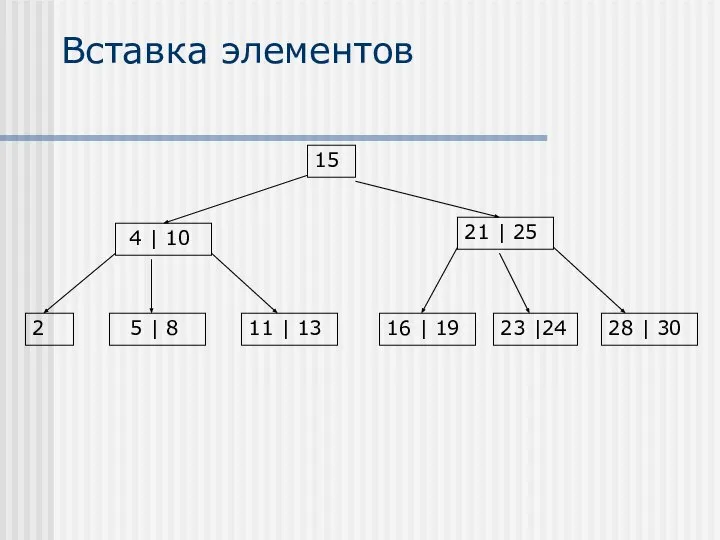
- 26. Вставка элементов 15 21 | 22 28 | 30 5 | 8 16 | 19 23
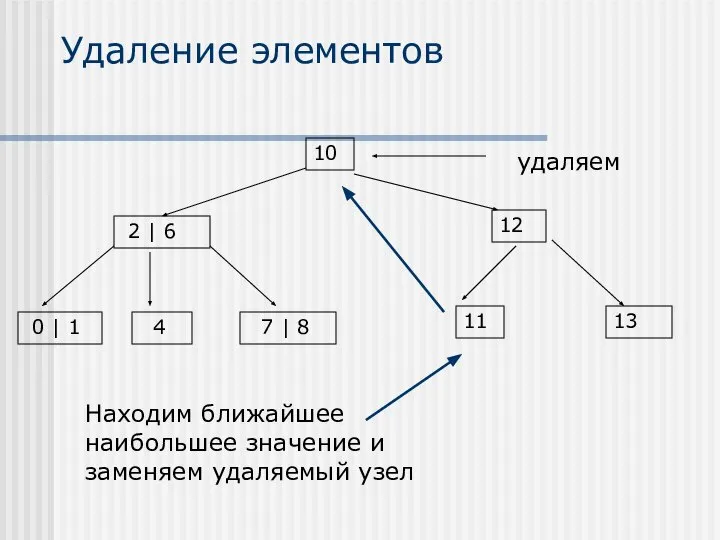
- 27. Удаление элементов Находим ближайшее наибольшее значение и заменяем удаляемый узел
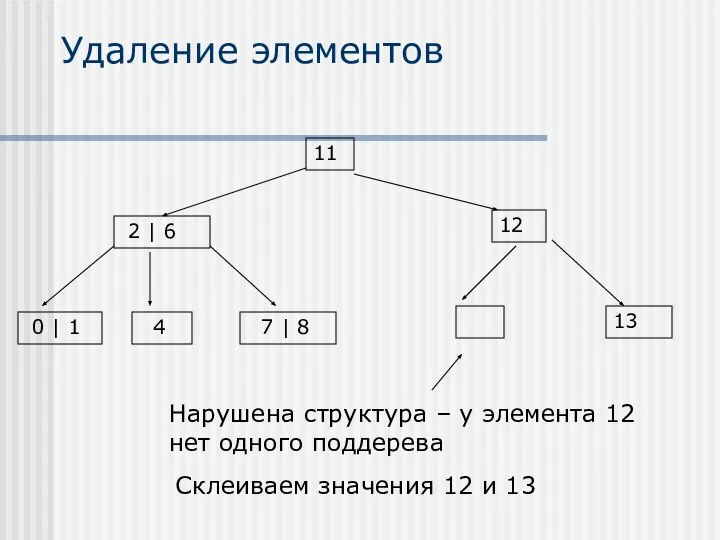
- 28. Удаление элементов Склеиваем значения 12 и 13
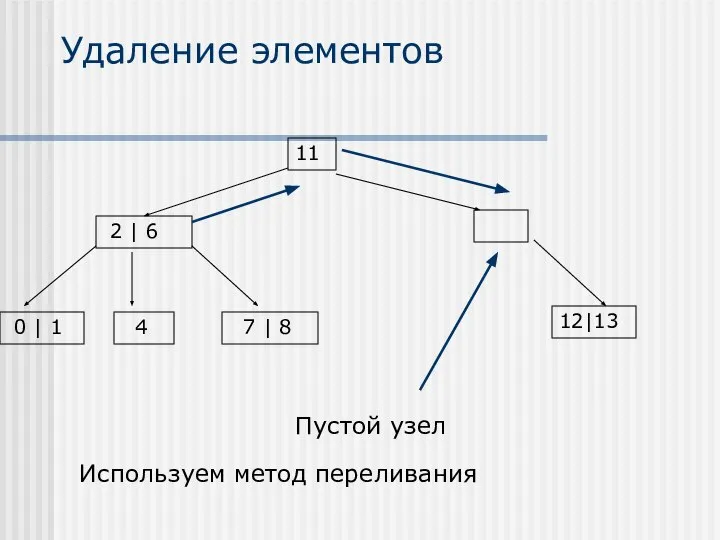
- 29. Удаление элементов Используем метод переливания
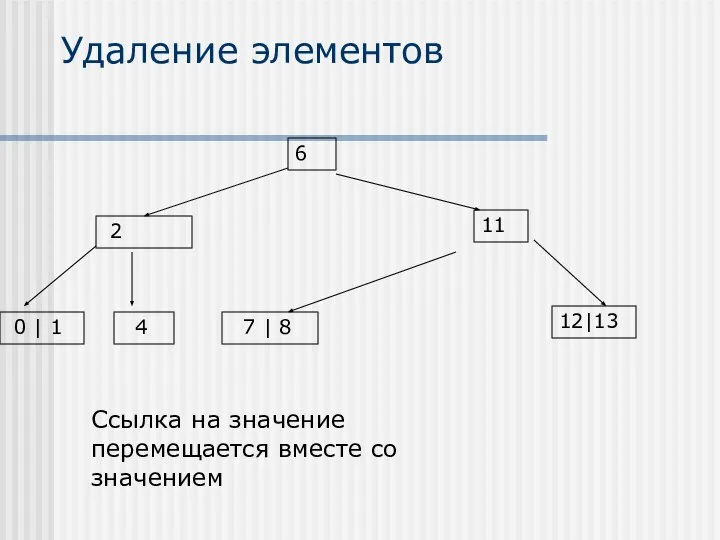
- 30. Удаление элементов 2 6 11 12|13 4 7 | 8 0 | 1 Ссылка на значение
- 31. Преимущества 2-3 дерева 2-3 дерево всегда сбалансировано Эффективность алгоритма поиска в таком дереве имеет порядок O(log2(N))
- 32. 2-3-4 деревья 2-3-4 дерево может содержать четырехместные узлы По сравнению с 2-3 деревом алгоритмы вставки и
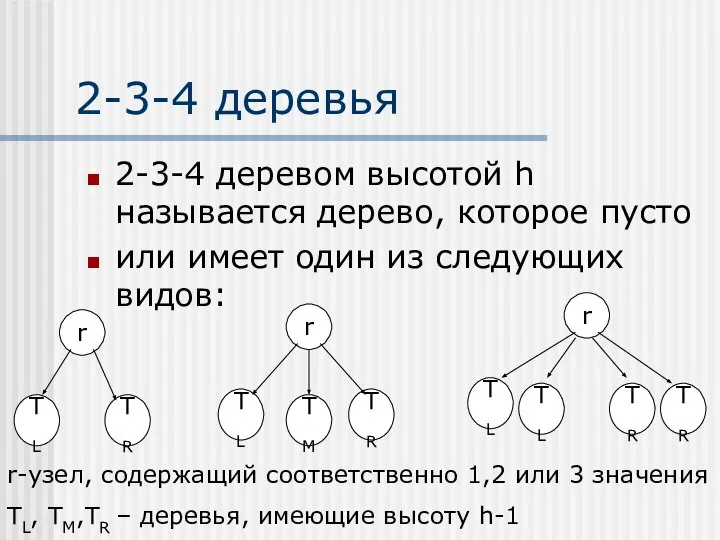
- 33. 2-3-4 деревья 2-3-4 деревом высотой h называется дерево, которое пусто или имеет один из следующих видов:
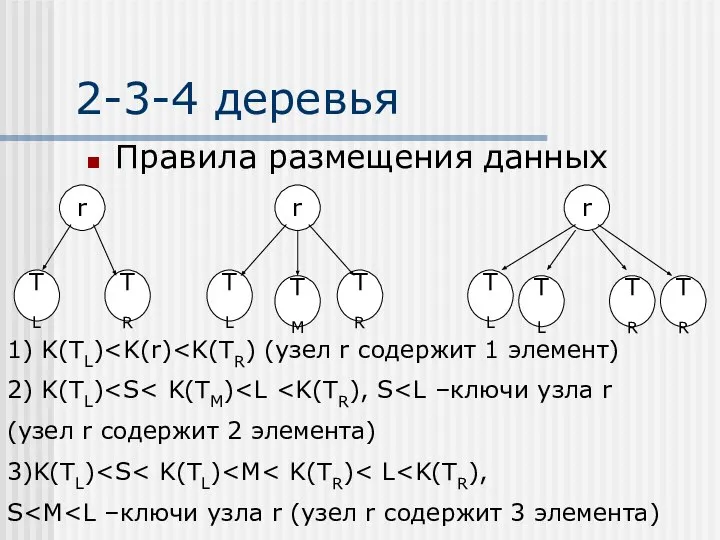
- 34. 2-3-4 деревья Правила размещения данных 1) K(TL) 2) K(TL) (узел r содержит 2 элемента) 3)K(TL) S
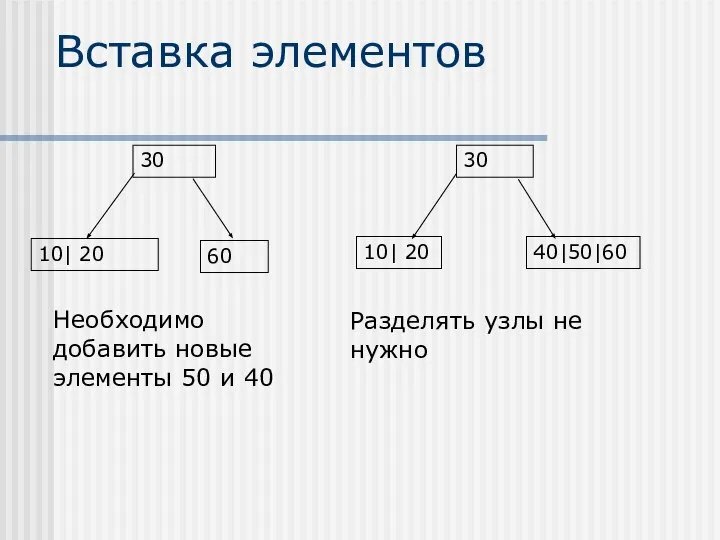
- 35. Вставка элементов Четырехместный узел разделяется сразу после обнаружения, при этом один из его элементов перемещается в
- 36. Вставка элементов
- 37. Вставка элементов
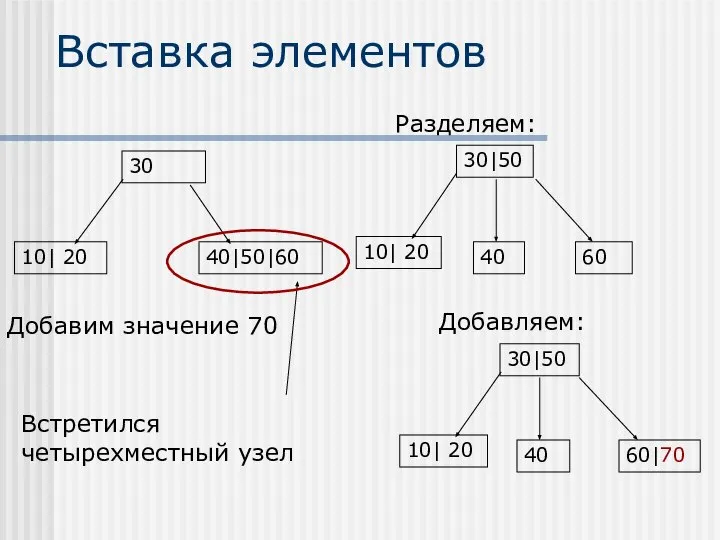
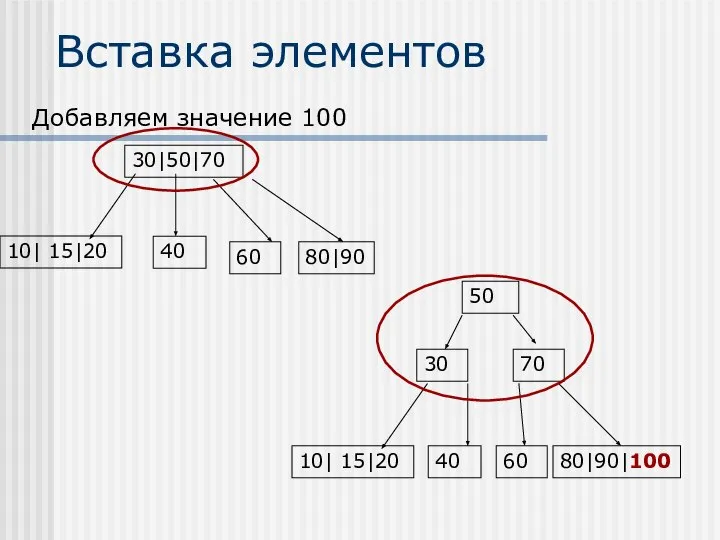
- 38. Вставка элементов Добавим значение 70
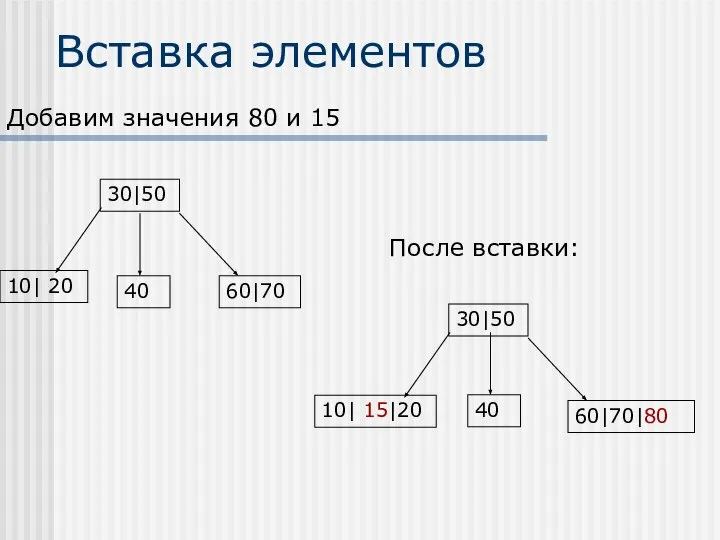
- 39. Вставка элементов Добавим значения 80 и 15
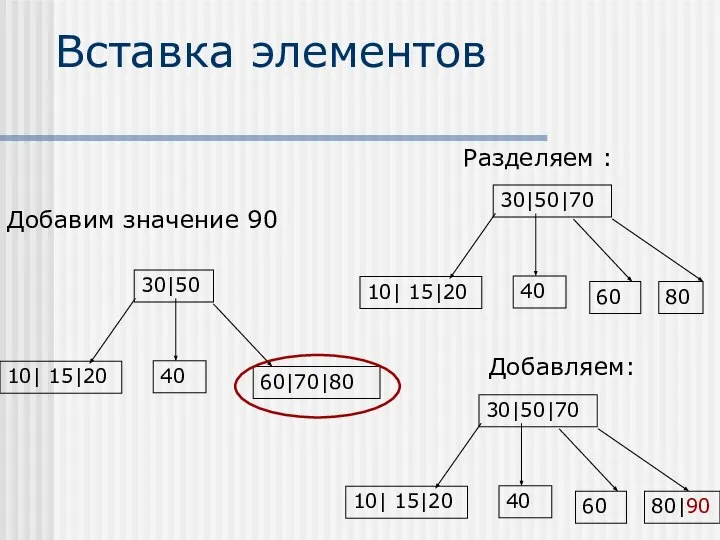
- 40. Вставка элементов
- 41. Вставка элементов
- 42. Разделение четырехместных узлов при вставке Возможны случаи: Узел является корнем Узел имеет двухместого родителя Узел имеет
- 43. Удаление элементов Находим узел, содержащий данный элемент Заменяем элемент его симметричным преемником (самый левый узел в
- 44. Удаление элементов При проходе дерева во время поиска элемента, необходимо сразу преобразовать каждый двухместный узел в
- 45. Заключение Достоинства 2-3 и 2-3-4 деревьев заключается в том, что они хорошо сохраняют баланс Алгоритмы вставки
- 47. Скачать презентацию



















 Политический анализ и политическое прогнозирование
Политический анализ и политическое прогнозирование Скоростносиловая подготовка в карате
Скоростносиловая подготовка в карате Проект «Жилой комплекс на Селезневской улице»
Проект «Жилой комплекс на Селезневской улице» Презентация на тему Творческий проект. Фартук.
Презентация на тему Творческий проект. Фартук.  Анализ результатов государственной итоговой аттестации по информатике в 2019 году
Анализ результатов государственной итоговой аттестации по информатике в 2019 году Задачи по управленческому учету
Задачи по управленческому учету Pitch deck. Re speecher
Pitch deck. Re speecher Законы рынка elena22_73@mail.ru
Законы рынка elena22_73@mail.ru По большому счету, БРЕНДИНГ решает все! HR-бренд или бренд работодателя это: Образ, имидж вашей компании как хорошего места работы в
По большому счету, БРЕНДИНГ решает все! HR-бренд или бренд работодателя это: Образ, имидж вашей компании как хорошего места работы в  Перетренированность
Перетренированность Основные положения теории линейной перспективы Выполнила: Заморина Марина 303 гр. Руководитель: кандидат педаг
Основные положения теории линейной перспективы Выполнила: Заморина Марина 303 гр. Руководитель: кандидат педаг Группа компаний «Метаком». Блоки вызова. Коммутаторы и разветвители. Блоки питания. Видеодомофоны. Ключи. Кнопки выхода. Замки
Группа компаний «Метаком». Блоки вызова. Коммутаторы и разветвители. Блоки питания. Видеодомофоны. Ключи. Кнопки выхода. Замки Азбука професий - презентация для начальной школы
Азбука професий - презентация для начальной школы Сынып сабақ жүйесі
Сынып сабақ жүйесі ИСКУССТВО КИНО Подготовила: Алмаева И.А., преподаватель МБОУ ДОД ДХШ №1 г.Жигулевск
ИСКУССТВО КИНО Подготовила: Алмаева И.А., преподаватель МБОУ ДОД ДХШ №1 г.Жигулевск Henry Mintzberg. Школа Конфигурации
Henry Mintzberg. Школа Конфигурации Схемы бернули. Предельные теоремы
Схемы бернули. Предельные теоремы 66b571e91b9d463687e67f779a4dcde1
66b571e91b9d463687e67f779a4dcde1 Конференция по духовно- нравственному воспитанию «Система духовно- нравственного воспитания в образовательном учре
Конференция по духовно- нравственному воспитанию «Система духовно- нравственного воспитания в образовательном учре Формы (источники) права. Тема 10
Формы (источники) права. Тема 10 Программирование на алгоритмическом языке БЕЙСИК
Программирование на алгоритмическом языке БЕЙСИК Презентация "Виртуальный музей «Мать и дитя»" - скачать презентации по МХК
Презентация "Виртуальный музей «Мать и дитя»" - скачать презентации по МХК Структура HTML документа. Представление текста в HTML документе
Структура HTML документа. Представление текста в HTML документе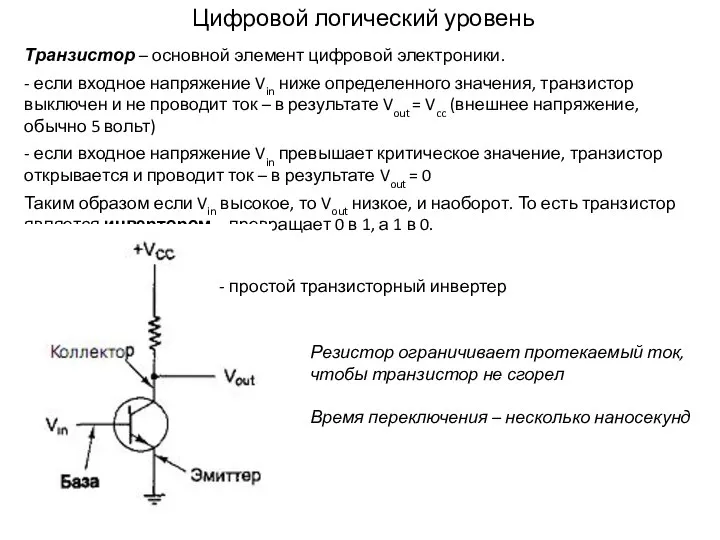 Цифровой логический уровень. Транзистор
Цифровой логический уровень. Транзистор Hurling. Purpose of game
Hurling. Purpose of game Политические партии и общественные объединения
Политические партии и общественные объединения Семинар «Основы туризма». Для представителей команд – участников туристического слета «Дорогами отцов-героев»
Семинар «Основы туризма». Для представителей команд – участников туристического слета «Дорогами отцов-героев» Бизнес план Тюменский автосборочный завод
Бизнес план Тюменский автосборочный завод