Содержание
- 2. Схема Бернулли Определение Схемой Бернулли называется последовательность независимых испытаний, в каждом из которых возможны лишь два
- 3. Теорема (формула Бернулли) Обозначим через m число успехов в n испытаниях схемы Бернулли. Тогда Доказательство Событие
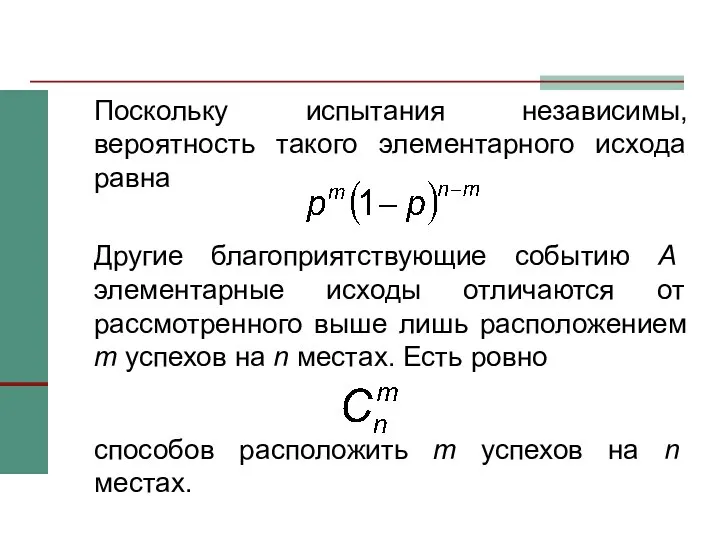
- 4. Поскольку испытания независимы, вероятность такого элементарного исхода равна Другие благоприятствующие событию A элементарные исходы отличаются от
- 5. Поэтому событие A состоит из элементарных исходов, вероятность каждого из которых равна т.е.
- 6. Наивероятнейшее число успехов В испытаниях схемы Бернулли наиболее вероятным числом успехов является a) единственное число m0
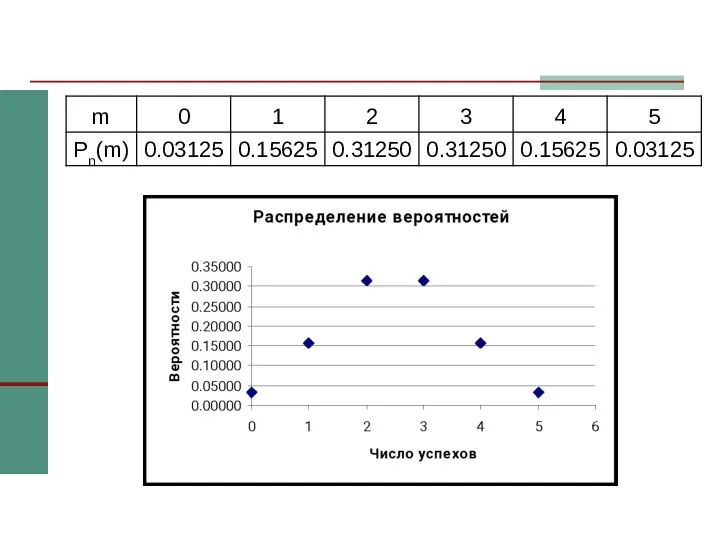
- 7. Пример Вычислить вероятности всех возможных значений появления «герба» при 5 бросаниях монеты. Построить график распределения этих
- 9. Наивероятнейшее число успехов: Вычисляем np + p = 5∙1/2 + ½ = 3. Это целое число,
- 11. Еще один пример Вероятность сдать экзамен равна 0,8. Найти наивероятнейшее число студентов, сдавших экзамен в группе
- 12. Полиномиальная схема Определение Полиномиальной схемой называется последовательность n независимых одинаковых испытаний, в каждом из которых возможны
- 13. Полиномиальная формула
- 14. Пример Человек с вероятностью 0,2 оказывается брюнетом, с вероятностью 0,4 —шатеном, с вероятностью 0,3 — блондином
- 15. Гипергеометрические испытания Пусть из совокупности n предметов, среди которых n1 предметов первого вида и n2 предметов
- 16. Гипергеометрические вероятности Данные испытания являются зависимыми.
- 17. Пример В урне 6 белых и 5 черных шаров. Из урны вынимают наугад 5 шаров. Найти
- 18. Теорема Пусть n → ∞ и n1→ ∞ так, что Тогда
- 19. Доказательство
- 20. Предельные теоремы для схемы Бернулли При числе испытаний, превышающем 20, вычисление точного значения Pn(m) затруднительно. В
- 21. Теорема Пуассона Если n → ∞, р → 0 так, что np → λ, 0
- 22. Доказательство Пусть np =λn. Тогда
- 23. При n → ∞, λn= np → λ
- 24. Следовательно,
- 25. Приближенная формула Пуассона где λ = np. Приближенную формулу Пуассона применяют при n > 30, р
- 26. Пример (дни рождения) Какова вероятность, что среди 500 случайно выбранных людей ни один не родился 1
- 27. По приближенной формуле Пуассона
- 28. Предельная теорема Муавра –Лапласа Если при n→ ∞ и постоянном р, не равном 0 или 1,
- 29. Доказательство этой теоремы основано на применении формулы Стирлинга
- 30. Локальная приближенная формула Муавра –Лапласа Локальную приближенную формулу Муавра – Лапласа применяют при n > 30,
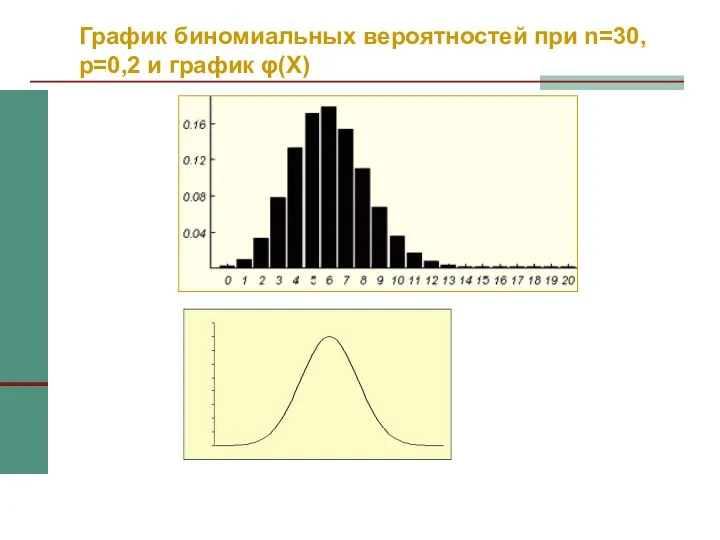
- 31. График биномиальных вероятностей при n=30, p=0,2 и график φ(X)
- 32. Интегральная предельная теорема Муавра –Лапласа При n→ ∞ и постоянном р, не равном 0 или 1,
- 33. Доказательство
- 34. По локальной предельной теореме
- 37. при n→ ∞ An →0
- 38. Интегральная приближенная формула Муавра –Лапласа Интегральную приближенную формулу Муавра – Лапласа применяют при n > 30,
- 39. Следствия
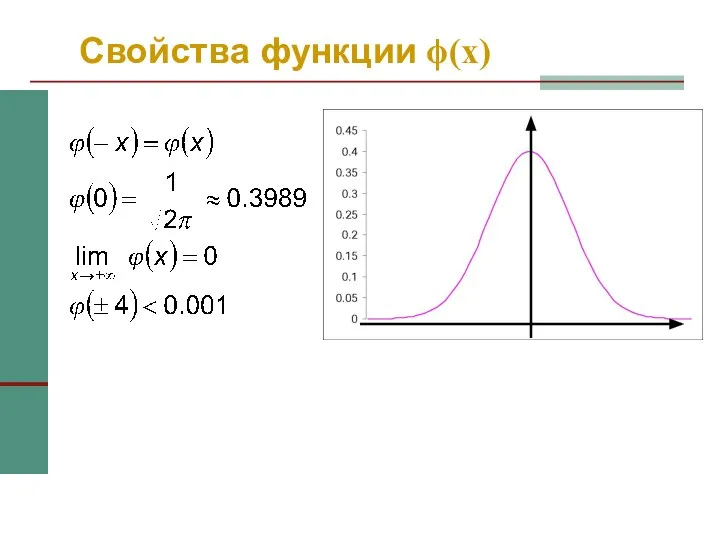
- 40. Свойства функции ϕ(x)
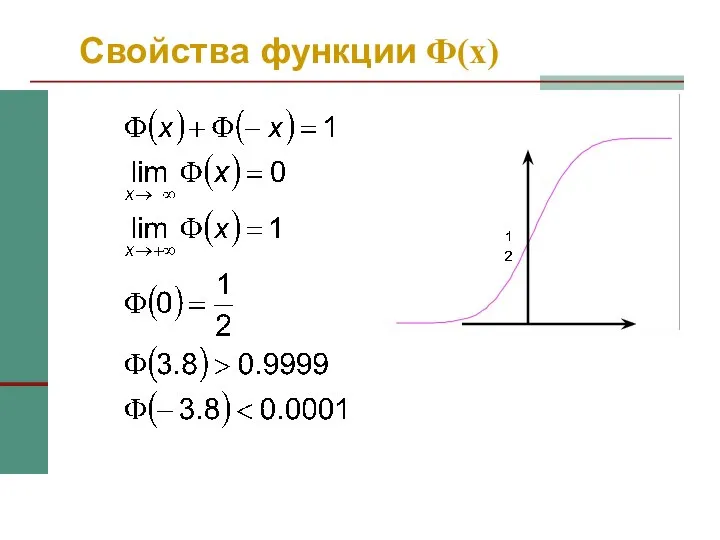
- 41. Свойства функции Ф(x)
- 42. Функция Лапласа Φ0(x). Вместо Φ(x) часто используют функцию Лапласа Φ0(x).
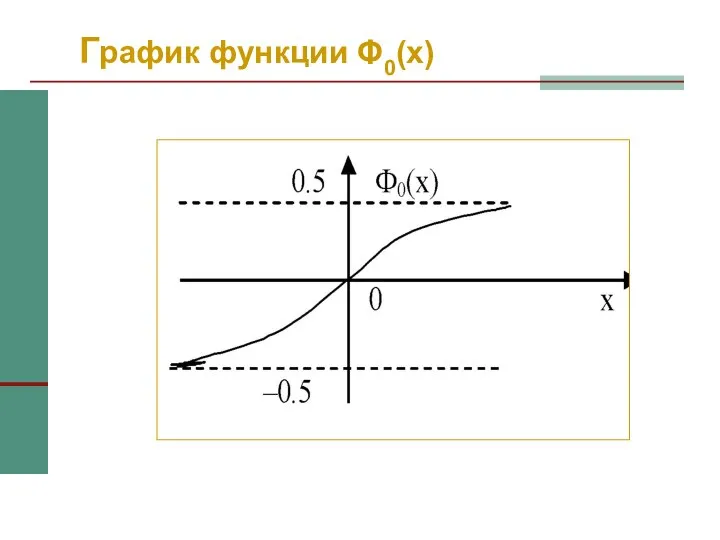
- 43. График функции Φ0(x)
- 44. Замечания поэтому в формулах может использоваться как Φ(x), так и Φ0(x). Значения функций находят в таблицах.
- 46. Скачать презентацию





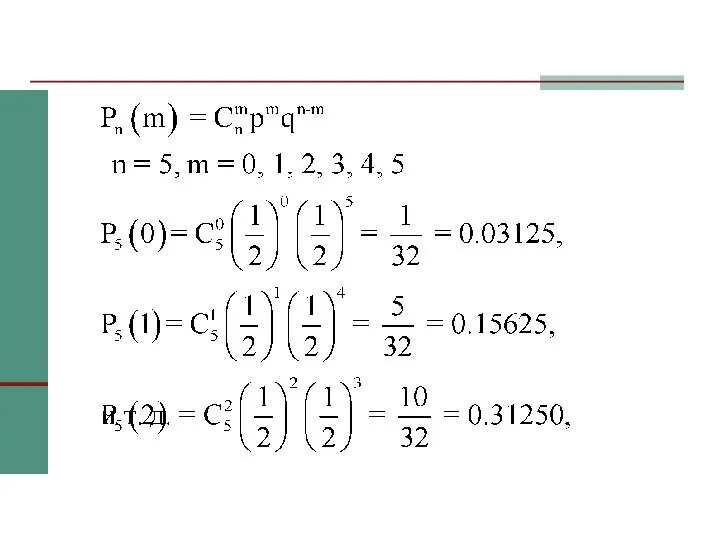
























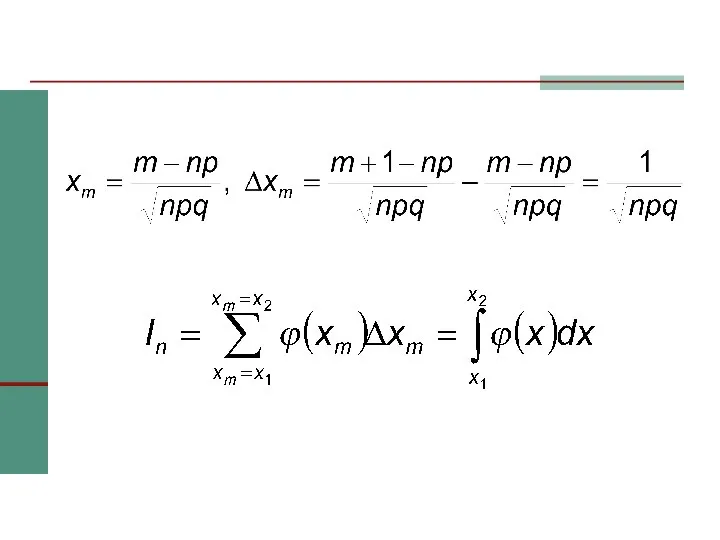
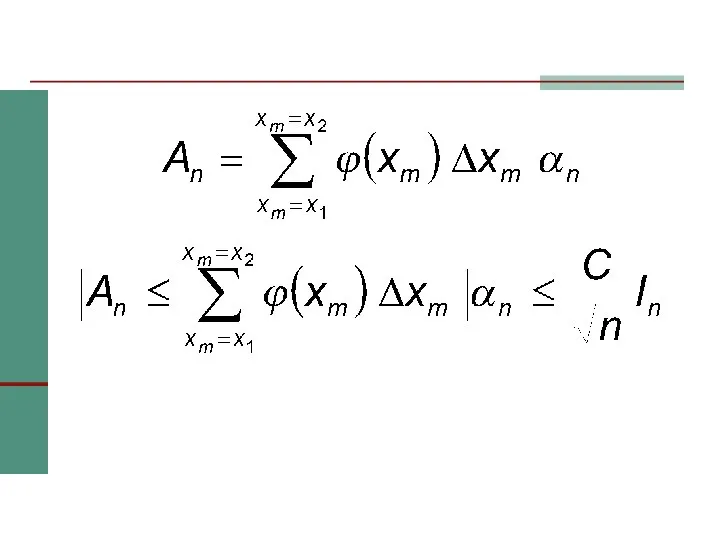
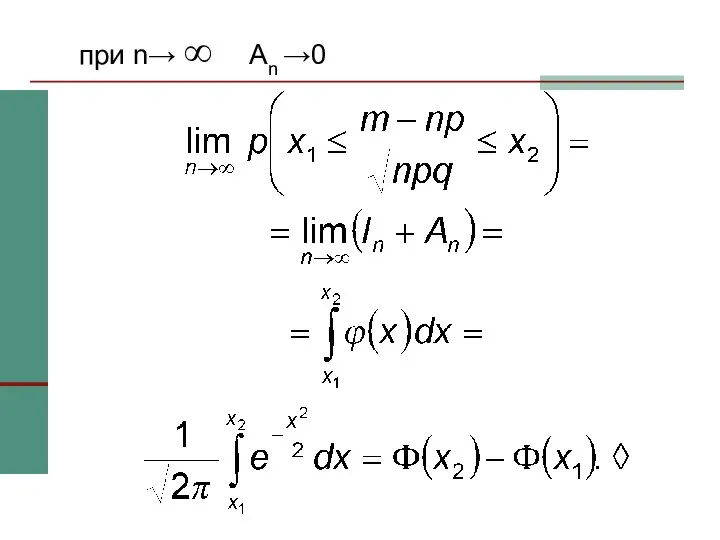




 Toyota. Motors: drive (x2) & lifting - block diagram
Toyota. Motors: drive (x2) & lifting - block diagram Перемены в культуре России в годы Петровских реформ
Перемены в культуре России в годы Петровских реформ Лето ягодное Часть 2 Презентацию подготовила С.Ф.Сироткина, учитель МОУ Уренской СОШ№1 Нижегородской области
Лето ягодное Часть 2 Презентацию подготовила С.Ф.Сироткина, учитель МОУ Уренской СОШ№1 Нижегородской области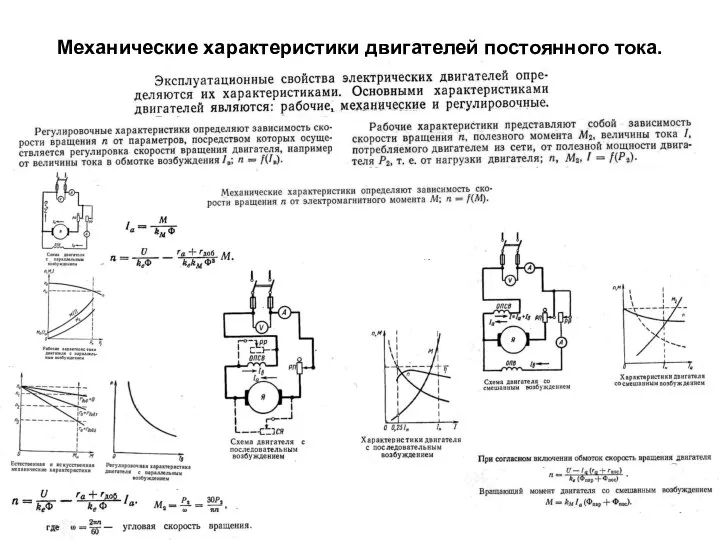 Механические характеристики двигателей постоянного тока. Судовые электрических системы. (Билет 19)
Механические характеристики двигателей постоянного тока. Судовые электрических системы. (Билет 19) E-pepper.Ru Остренький интернет бизнес!
E-pepper.Ru Остренький интернет бизнес! Подготовка и замена расходомера
Подготовка и замена расходомера Политические организации и политические движения
Политические организации и политические движения Физиол пищеварения,нормы питания
Физиол пищеварения,нормы питания Презентация Министерство Финансов
Презентация Министерство Финансов 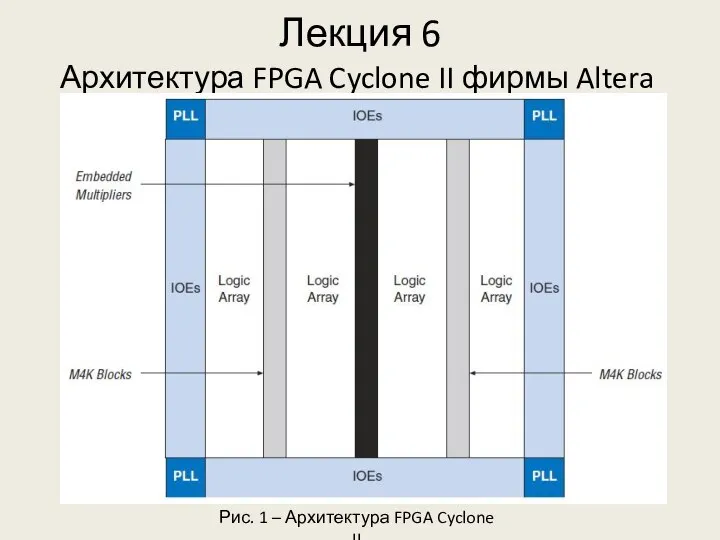 Архитектура FPGA Cyclone II фирмы Altera
Архитектура FPGA Cyclone II фирмы Altera Генеральное соглашение по торговле услугами(ГАТС) Ходиев.Ф.Б Т-093
Генеральное соглашение по торговле услугами(ГАТС) Ходиев.Ф.Б Т-093  10 ошибок в воспитании, которые все когда-нибудь совершали Родительский всеобуч
10 ошибок в воспитании, которые все когда-нибудь совершали Родительский всеобуч Особенности этики делового общения в Японии
Особенности этики делового общения в Японии Я і мае сябры. Беларускія імёны. (Тэма 11)
Я і мае сябры. Беларускія імёны. (Тэма 11) Презентация на тему "Сущность, движущие силы, противоречия и логика образовательного процесса. Закономерности и принципы обуче
Презентация на тему "Сущность, движущие силы, противоречия и логика образовательного процесса. Закономерности и принципы обуче Презентация Правовые и нормативные основы охраны труда
Презентация Правовые и нормативные основы охраны труда Матвеева. Жуковский. 2019
Матвеева. Жуковский. 2019 ПАРЕНХИМАТОЗНЫЕ ДИСТРОФИИ
ПАРЕНХИМАТОЗНЫЕ ДИСТРОФИИ Модель лидерства «путь — цель» Хауза и Митчелла
Модель лидерства «путь — цель» Хауза и Митчелла Лекарственные средства, влияющие на агрегацию тромбоцитов, свертывание крови и фибринолиз
Лекарственные средства, влияющие на агрегацию тромбоцитов, свертывание крови и фибринолиз Краски природы Презентация учителя начальных классов МБОУ «СОШ №4» г. Новочебоксарска Гладковой Надежды Анатольевны._
Краски природы Презентация учителя начальных классов МБОУ «СОШ №4» г. Новочебоксарска Гладковой Надежды Анатольевны._ Творческая работа «6 А» класса (гимназия) Долаберидзе
Творческая работа «6 А» класса (гимназия) Долаберидзе День народного единства - презентация для начальной школы
День народного единства - презентация для начальной школы И.А.Крылов «Чиж и голубь» 3 класс Учитель начальных классов МКОУ «ТШИ», п. Тазовский Беспалая Ирина Феликсовна
И.А.Крылов «Чиж и голубь» 3 класс Учитель начальных классов МКОУ «ТШИ», п. Тазовский Беспалая Ирина Феликсовна Анализ деятельности Уинстона Черчилля в контексте личного PR (самопиар)
Анализ деятельности Уинстона Черчилля в контексте личного PR (самопиар) Ұйымдасқан қылмыстылықтың алдын алу
Ұйымдасқан қылмыстылықтың алдын алу Открытый конкурс в электронной форме МИР 2019
Открытый конкурс в электронной форме МИР 2019 Летучка
Летучка