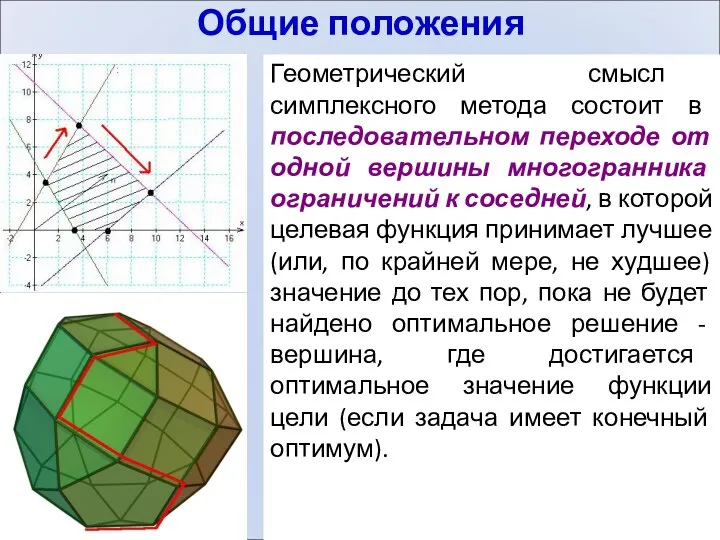
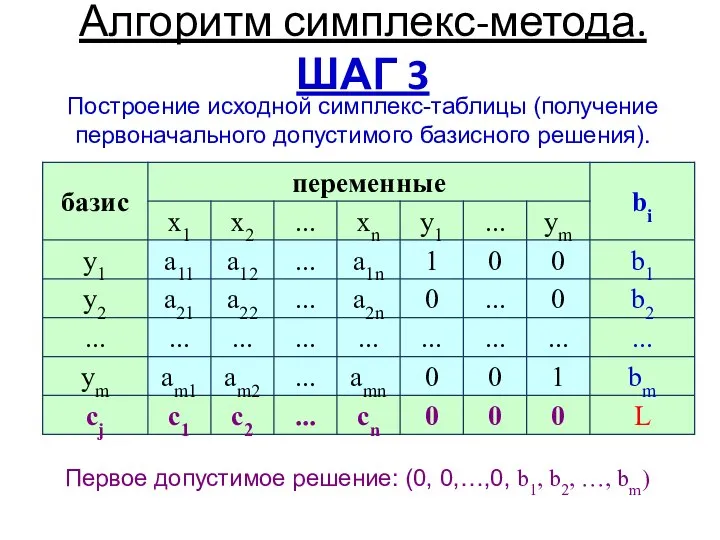
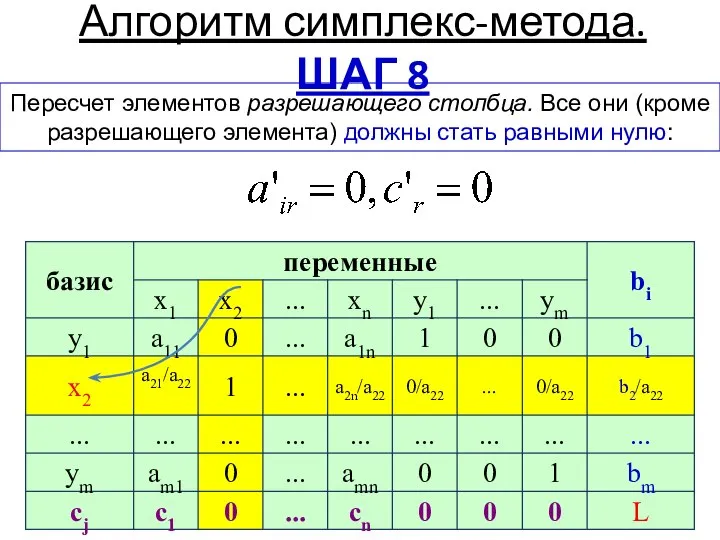
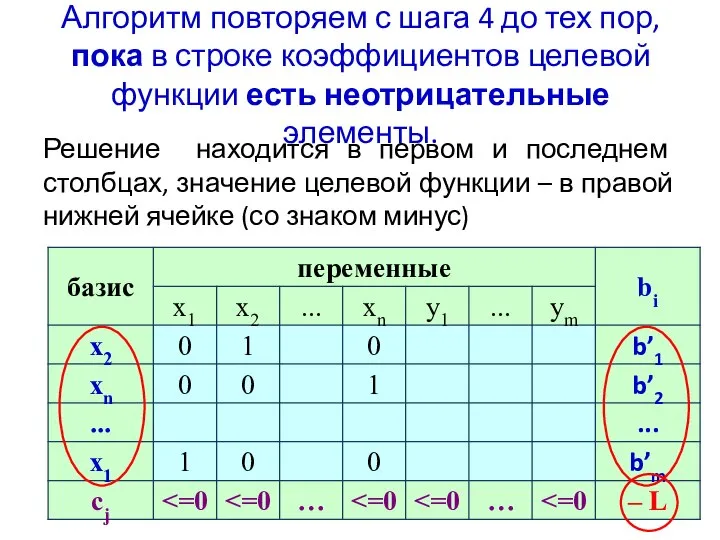
Симплекс-метод

1947 г. американским математиком Дж. Данцигом

Джорд Бернард Данциг (George Bernard Dantzig; 1914 —2005) — выдающийся математик США. Разработал симплексный алгоритм, применяемый при решении задач линейного программирования. Считается «отцом линейного программирования», наряду с советским математиком Л. В. Канторовичем.

Леонид Витальевич Канторович (1912-1986) — советский математик, создатель математической экономики и линейного программирования. Работал в области функционального анализа, вычислительной математики, теории программирования, математической физики и в экономике.

принял написанные на доске уравнения за домашнее задание. Оно показалось ему сложнее обычного, но через несколько дней Бернард всё-таки смог его выполнить. Оказалось, что это были «нерешаемые в то время» задачи по статистике, над решением которых работали многие учёные.

Вспоминают, что когда Канторович пришёл на свою первую лекцию, студенты дружелюбно закричали ему: «Парень, садись на место! Сейчас профессор придет» Что неудивительно, поскольку «профессору» в это время было 18 лет. Пишут, что он был не очень блестящим лектором, но пытался добросовестно донести до студентов глубинный смысл математических определений и теорем. Экзаменатором он был строгим и требовательным, что, наверное, свойственно для многих вундеркиндов, которые очень многое схватывают на лету и не прощают студентам тупости.

Король Швеции Карл XVI Густав вручает Л.В.Канторовичу Нобелевскую премию

Присуждение премии Дж. Данцигу

вершины многогранника ограничений к соседней, в которой целевая функция принимает лучшее (или, по крайней мере, не худшее) значение до тех пор, пока не будет найдено оптимальное решение - вершина, где достигается оптимальное значение функции цели (если задача имеет конечный оптимум).

какого-либо первоначального допустимого базисного решения задачи;
2) правило перехода к лучшему (точнее, не худшему) решению;
3) критерий проверки оптимальности найденного решения.

определенности будем считать, что решается задача на отыскание максимума.
L(x) = c1x1 + c2x2 + ... + cnxn ?max;
a11x1 + a12x2 + ... + a1nxn ≤ b1,
a21x1 + a22x2 + ... + a2nxn ≤ b2,
...  
am1x1 + am2x2 + ... + amnxn ≤ bm;
xj ≥ 0, j = 1,n    

канонической форме (перевод функциональных ограничений в систему уравнений).

Все дополнительные переменные также должны быть неотрицательными и иметь тот же знак, что и свободные члены системы ограничений.

bm)

Построение исходной симплекс-таблицы (получение первоначального допустимого базисного решения).

разрешающего столбца
(переменной, вводимой в базис).

Алгоритм симплекс-метода. ШАГ 5

Проверка условия: все cj ≤ 0. Если НЕТ - осуществляется переход к шагу 5, если ДА - задача решена.

задача неразрешима.

Алгоритм симплекс-метода. ШАГ 6

Проверка условия: все air ≤ 0. Если ДА - целевая функция неограничена и решения нет, если НЕТ - переход к шагу 7.

Алгоритм симплекс-метода. ШАГ 7

Выбор разрешающей строки (переменной, выводимой из базиса) по условию:

для air > 0, где s - номер разрешающей строки.

новые значения пересчитываемых элементов,
asj , bs - старые значения пересчитываемых элементов,
asr - старое значение разрешающего элемента.
Таким образом, при пересчете элементов разрешающей строки каждый ее элемент делится на разрешающий элемент.

Алгоритм симплекс-метода. ШАГ 8

Пересчет элементов симплекс-таблицы (переход к новому базисному решению).
Порядок пересчета различных элементов таблицы несколько отличается.

Для элементов разрешающей строки используются следующие формулы:

элемента) должны стать равными нулю:

прямоугольника: мысленно выделяется прямоугольник, в котором элемент, подлежащий пересчету и разрешающий элемент образуют одну из диагоналей. Формулы будут иметь следующий вид:

Алгоритм симплекс-метода. ШАГ 8

Пересчет остальных элементов

коэффициентов целевой функции есть неотрицательные элементы.

Решение находится в первом и последнем столбцах, значение целевой функции – в правой нижней ячейке (со знаком минус)