Содержание
- 2. Введение 1. Основные понятия статики 1.1. Абсолютно твёрдое тело 1.2. Свободное (несвободное тело) 1.3. Сила. Система
- 3. 3.1. Приведение сходящейся системы сил к центру 3.2. Условия равновесия сходящейся системы сил 3.3. Теорема о
- 4. 6. Связи. Силы реакций связей 5.5. Уравнения равновесия плоской произвольной системы сил 7. Решение задач статики
- 5. Введение Наука о механическом движении и взаимодействии материальных тел называется теоретической механи-кой. Механическим движением называют происходящее
- 6. Круг проблем, рассматриваемых в механике, очень велик и с развитием этой науки в ней появился целый
- 7. При изучении какого-либо явления необходимо выделять в нём наиболее существенное, главное, абстрагируясь от других незначительных сторон
- 8. Таковыми и являются законы, теоремы и принципы теоретической механики, которые установлены в результате обобщения результате многочисленных
- 9. Статика твёрдого тела Статика – это раздел теоретической механики, в котором изучаются методы эквивалентных преобразо-ваний систем
- 10. Преобразование систем сил, действующих на твёрдое тело, в эквивалентные им системы сил простейшего вида. Задачи статики
- 11. Абсолютно твёрдое тело – совокупность матери-альных точек, в которой расстояние между двумя любыми точками остаётся неизменным.
- 12. Абсолютно твёрдое тело (в дальнейшем твёрдое тело или тело) называется свободным, если его перемещения из данного
- 13. Тело, перемещениям которого в пространстве препятствуют другие тела, называется несвободным, рис. 2.
- 14. 1.3. Сила. Система сил Состояние покоя или движения тела зависит от характера его механического взаимодействия с
- 18. 1.4. Проекция силы на ось Проекция силы на ось есть алгебраическая вели-чина, равная произведению модуля силы
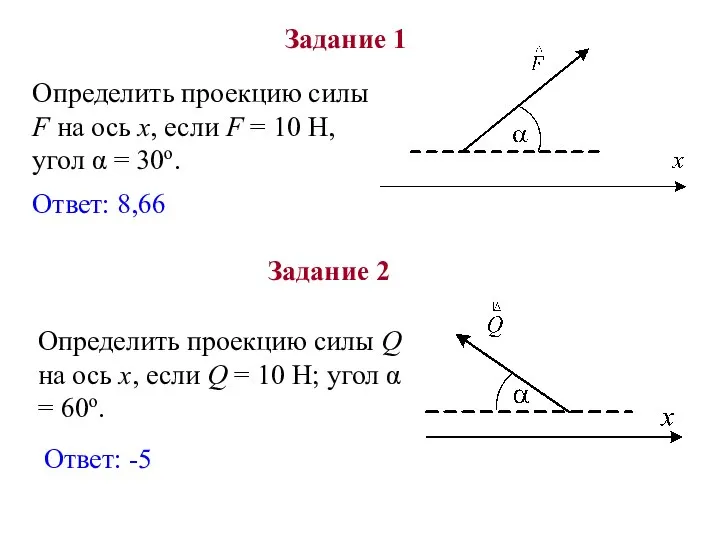
- 19. Пример 1
- 20. Определить проекцию силы F на ось x, если F = 10 H, угол α = 30o.
- 21. 1.5. Определение модуля силы
- 22. Пример 2 Определить модуль и направление силы, если её проекции на координатные оси равны: Fx =
- 23. Направляющие косинусы: Углы в радианах между вектором силы и координатными осями: Углы в градусах:
- 24. Задание 3 Определить модуль и направление силы, если её проекции на координатные оси равны: Fx =
- 25. 1.6. Главный вектор системы сил Вектор, равный геометрической сумме векторов сил, системы, называется главным вектором этой
- 26. Направление главного вектора определяется направ-ляющими косинусами
- 27. Задание 4 Определить модуль главного вектора сходящихся системы сил F1 = 10 H, F2 = 15
- 28. Решение (С использованием пакета Mathcad)
- 29. Моментом силы относительно точки О называется вектор равный векторному произведению радиус-вектора точки приложения силы относительно точки
- 30. Вектор момента приложен в точке О и направлен перпендикулярно плоскости, прохо-дящей через центр О и силу
- 31. Модуль вектора момента равен где h – плечо силы (длина перпендикуляра, опущенного из точки О на
- 33. Для сил, расположенных в одной плоскости применяется алгебраический момент. Алгебраическим моментом силы относительно точки на плоскости
- 34. Момент считается положительным, когда сила стремится повернуть тело вокруг центра О против хода часовой стрелки. Свойства
- 35. 2) момент силы относительно точки равен нулю, когда линия действия силы проходит через эту точку (плечо
- 36. Пример 3 Балка АС находится в равновесии под действием системы сил, приведенной на рисунке. Определить сумму
- 37. Решение
- 38. Моменты сил XA, YA равны нулю, так как линии их действия пересекают моментную точку А. Чтобы
- 39. Находим моменты этих сил относительно точки А. Находим сумму моменты сил. Сумма моментов сил относительно точки
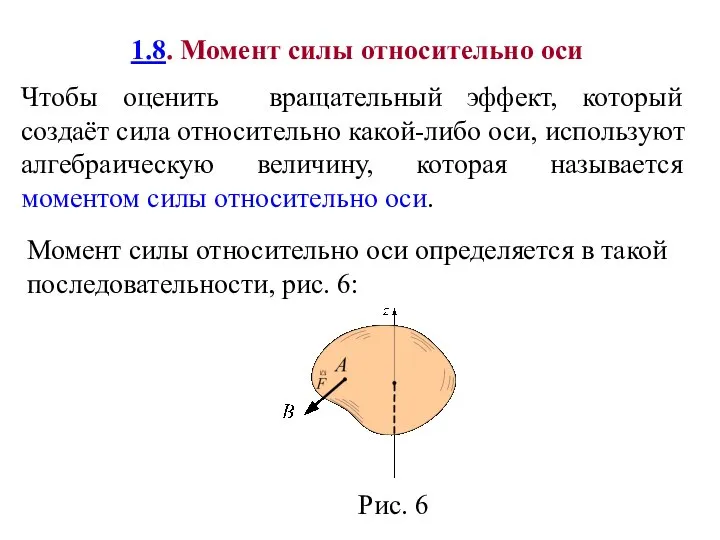
- 40. 1.8. Момент силы относительно оси Чтобы оценить вращательный эффект, который создаёт сила относительно какой-либо оси, используют
- 41. строим плоскость, перпендикулярную оси;
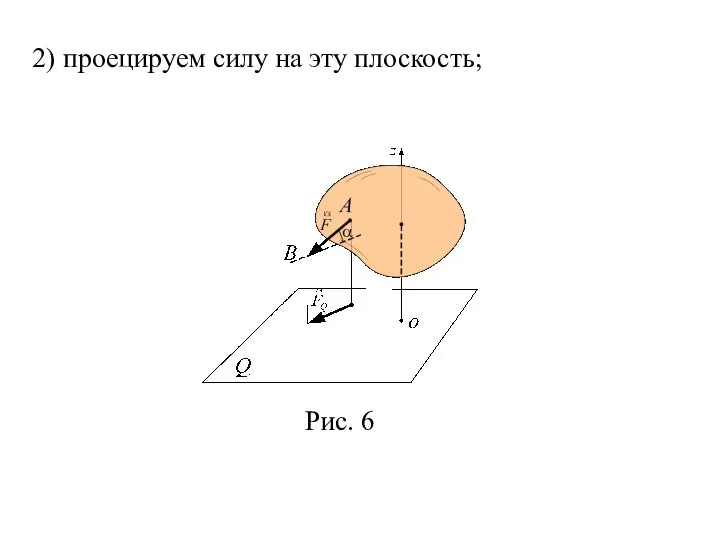
- 42. 2) проецируем силу на эту плоскость;
- 43. 3) находим плечо проекции силы относительно точки пересечения оси с плоскостью;
- 44. 4) вычисляем произведение проекции силы на плечо; 5) определяем знак момента. Момента силы имеет знак (+),
- 45. Момент силы относительно оси равен нулю, если: сила параллельна оси; линия действия силы пересекает ось.
- 46. Момент силы относительно точки связан с моментом силы относительно оси, проходящей через эту точку следующим соотношением:
- 47. Если известны углы которые составляет векторный момент силы относительно точки с координатными осями, то её моменты
- 48. Зная моменты силы относительно координатных осей, найдём модуль момента силы относительно точки по формуле: где α,
- 49. 1.9. Главный момент системы сил
- 50. Направление главного момента определяется направ-ляющими косинусами
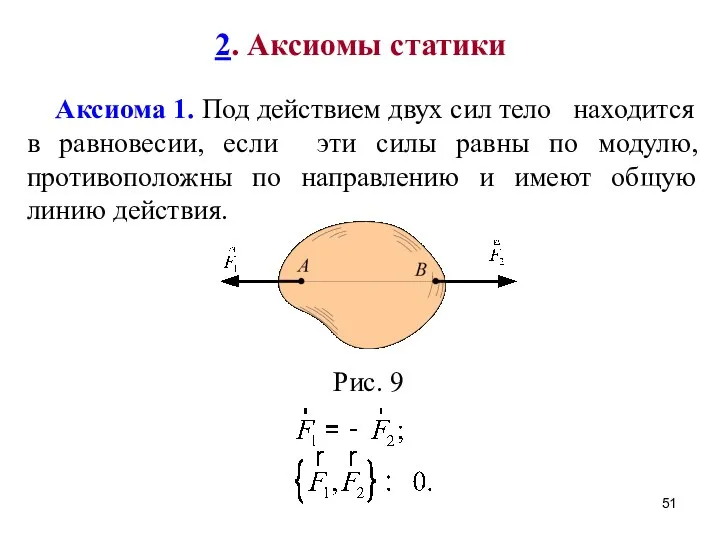
- 51. Аксиома 1. Под действием двух сил тело находится в равновесии, если эти силы равны по модулю,
- 52. Аксиома 2. Действие данной системы сил на абсолютно твердое тело не изменится, если к ней прибавить
- 53. Аксиома 3. Две силы, приложенные к телу в одной точке, имеют равнодействующую, прило-женную в той же
- 54. Рис. 12 На первом рисунке равнодействующая двух сил приложена в точке А. На втором рисунке система
- 55. Модуль равнодействующей силы вычисляется по формуле
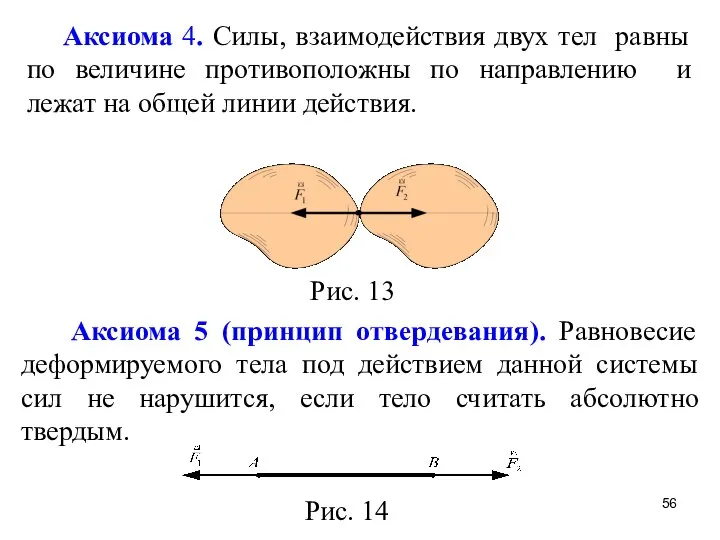
- 56. Аксиома 4. Силы, взаимодействия двух тел равны по величине противоположны по направлению и лежат на общей
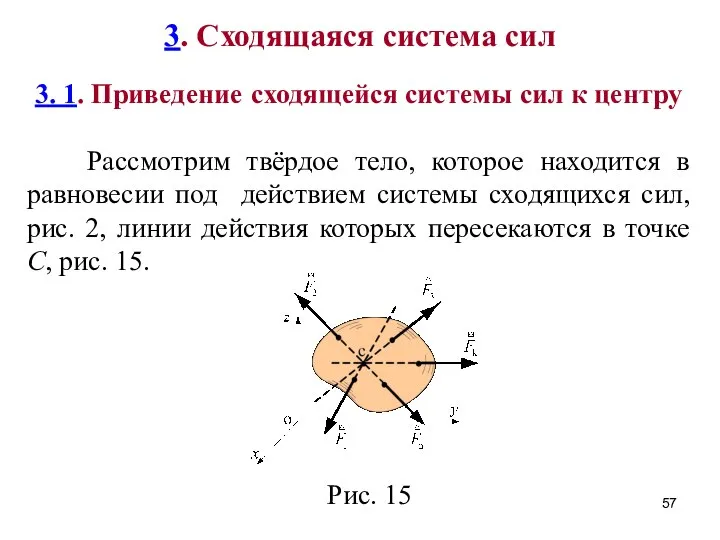
- 57. 3. Сходящаяся система сил 3. 1. Приведение сходящейся системы сил к центру Рассмотрим твёрдое тело, которое
- 58. Приведём эту систему сил к центру С. Для этого применим следствие из второй аксиомы статики и
- 59. Таким образом, сходящаяся система сил приводится к одной силе – равнодействующей, приложенной в точке пересечения линий
- 60. 3. 2. Условия равновесия сходящейся системы сил Рассмотрим твёрдое тело, которое находится в равновесии под действием
- 61. В результате получим векторное условие равно-весия сходящейся системы сил: для того чтобы тело под действием сходящейся
- 62. Так как главный вектор равен геометрической сумме сил, то эта сумма также будет равна нулю Складывая
- 63. Введём координатные оси Оxyz и спроецируем векторную сумму сил на эти оси. В результате приходим к
- 64. Если тело находится в равновесии под действием плоской сходящейся системы сил, рис. 18 то для неё
- 65. 3.3. Теорема о трёх силах Теорема. Если тело находится в равновесии под действием трех непараллельных сил,
- 66. 4. Теория пар сил Парой сил называется система двух параллельных, равных по модулю и противоположных по
- 67. Плоскость, проходящая через лини действия сил пары, называется плоскостью действия пары. Расстояние h между линиями действия
- 68. Пары, расположенные в одной плоскости образуют плоскую систему пар, рис. 22. Пары, расположенные в пространстве произвольным
- 69. Действие пары сил на твёрдое тело сводится к вращательному эффекту, мерой которого является момент пары. 4.2.
- 70. Главный момент пары сил относительно центра О равен:
- 73. и направлен перпендикулярно плоскости действия пары сил, рис. 25, 26. Таким образом момент пары сил равен
- 76. 1) модуль момента пары равен произведению силы пары на её плечо; Из векторного выражения момента пары
- 77. 2) вектор момента пары направлен перпендикулярно плоскости действия пары в ту сторону, откуда видно, что пара
- 78. 3) момент пары не зависит от положения пары относительно центра О и, следовательно, вектор момента пары
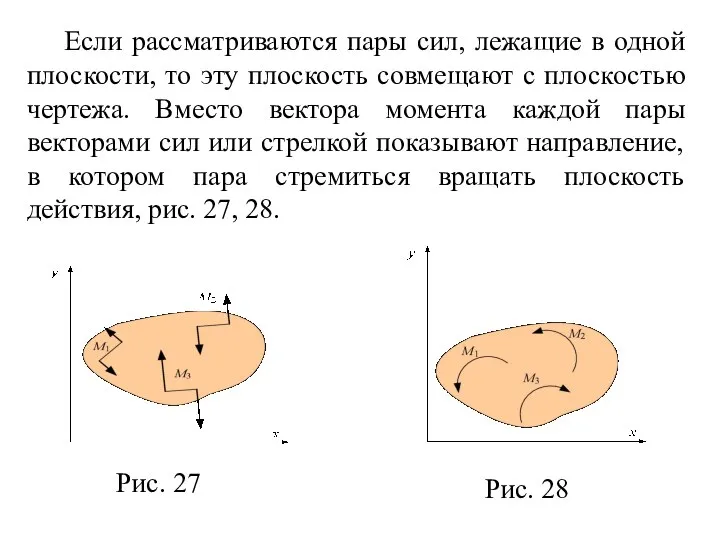
- 79. Если рассматриваются пары сил, лежащие в одной плоскости, то эту плоскость совмещают с плоскостью чертежа. Вместо
- 80. Момент считается положительным, если пара стремится вращать плоскость действия против хода часовой стрелки. В противном случае
- 81. 1) при переносе пары сил куда угодно в плоскости её действия; Из доказанного следует, что момент
- 83. 2) при повороте пары сил в плоскости её действия;
- 84. 3) при переносе пары сил из плоскости её действия в параллельную плоскость.
- 85. 4.3. Сложение моментов пар сил Рассмотрим систему пар сил, плоскости действия которых расположены произвольно в пространстве,
- 86. Векторы моментов пар – свободные векторы. Поэтому выберем произвольную точку С и перенесём моменты пар в
- 87. Складывая векторы моментов пар, получим многоугольник, замыкающей стороной которого будет момент пары, эквивалентной данной системе пар.
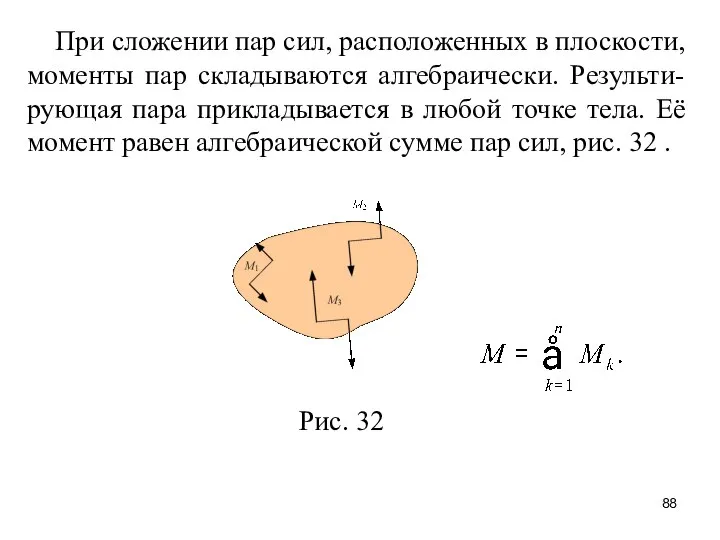
- 88. При сложении пар сил, расположенных в плоскости, моменты пар складываются алгебраически. Результи-рующая пара прикладывается в любой
- 89. 4.4. Условия равновесия пар сил Если тело находится в равновесии под действием произвольной системы пар, то
- 90. Если тело находится в равновесии, под действием системы пар, расположенных в одной плоскости, то алгебраическая сумма
- 91. 5.1. Теорема о параллельном переносе силы Рассмотрим тело, на которое действует сила, прило-женная в точке А,
- 93. Таким образом, силу, не изменяя её действия на тело, можно переносить параллельно самой себе в любую
- 94. 5.2. Теорема о приведении системы силы к центру Рассмотрим твёрдое тело, на которое действует произвольная пространственная
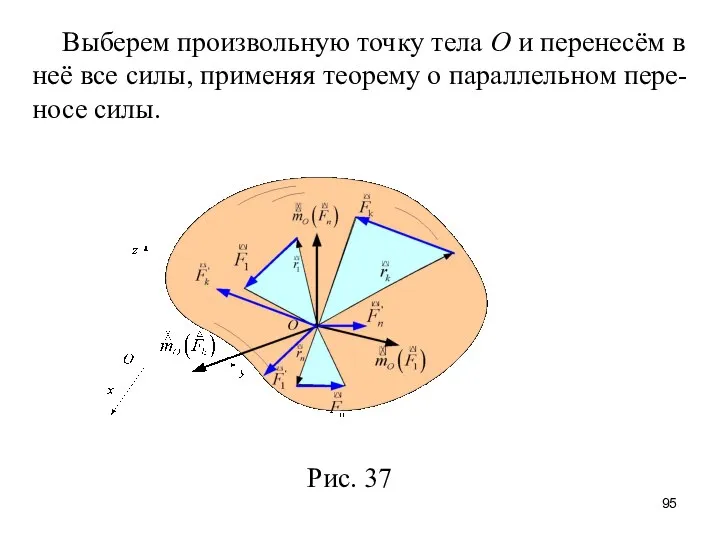
- 95. Выберем произвольную точку тела О и перенесём в неё все силы, применяя теорему о параллельном пере-носе
- 96. В результате в точке О будут приложены две группы векторов:
- 97. Таким образом: любую произвольную систему сил, действующую на твёрдое тело, можно заменить одной силой, равной главному
- 99. 5.3. Условия равновесия произвольной системы сил Рассмотрим твёрдое тело, которое находится в равновесии под действием произвольной
- 100. Из приведенных равенств следует: Таким образом, для того чтобы тело под действием произвольной системы сил находилось
- 101. 5.4. Уравнения равновесия произвольной системы сил Запишем условия равновесия произвольной системы сил. Главный вектор и главный
- 102. Таким образом, если тело под действием приложенной к нему системы сил находится в равновесии, то векторная
- 103. Построим декартова координатные оси с началом в центре приведения сил. Спроецируем на эти оси векторные равенства:
- 104. В результате получим:
- 105. Используя связь между моментом силы относительно точки и моментом силы относительно оси, проходящей через эту точку,
- 106. Таким образом, если твёрдое тело находится в равновесии под действием произвольной системы сил, то для неё
- 107. 5.5. Уравнения равновесия плоской произвольной системы сил Система сил, линии действия которых расположены произвольно в одной
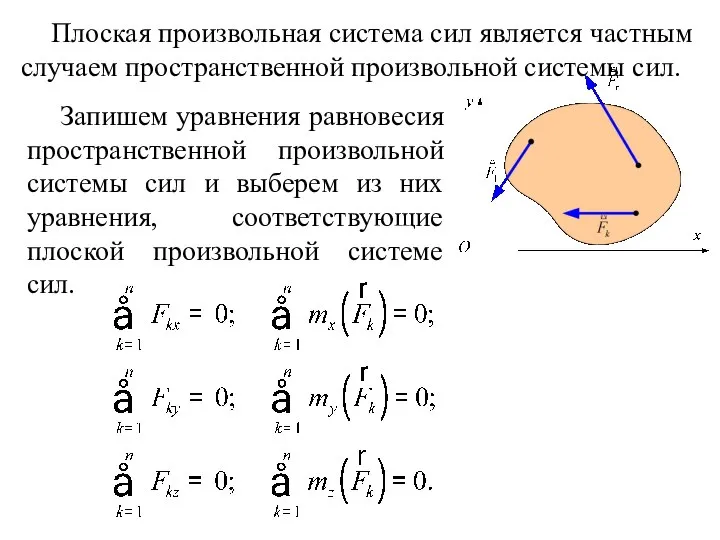
- 108. Плоская произвольная система сил является частным случаем пространственной произвольной системы сил. Запишем уравнения равновесия пространственной произвольной
- 109. Таким образом, если твёрдое тело находится в равновесии под действием плоской произвольной системы сил, то для
- 110. Из представленных уравнений три уравнения для плоской произвольной системы сил являются тождествами: Так как на плоскости
- 111. Здесь А, В, С – три произвольных центра, не лежащие на одной прямой.
- 112. 6. Связи и силы реакций связей Свободное тело – твёрдое, не закреплённое тело, которому можно сообщить
- 113. Сила реакции связи – сила, с которой связь дей-ствует на рассматриваемое тело. Направление силы реакции связи.
- 114. Если гладкое тело опирается на ребро, то сила реакции направлена по нормали к поверхности тела, рис.
- 115. При действии тела ребром на гладкую поверхность сила реакции направлена по нормали к поверхности связи, рис.
- 116. Рис. 47 На практике сила реакции заменяется ее составляю- щими, направленными в стороны положительных направлений координатных
- 117. Шарнирная подвижная опора - подвижная опора (на роликах, скользящая), снабженная цилиндрическим шарниром. Сила реакции шарнирной подвижной
- 118. Сферический шарнир - устройство, обеспечиваю-щее движение тела вокруг одной его неподвижной точки. Сила реакции сферического шарнира
- 119. Невесомый стержень – это стержень, весом которого по сравнению с воспринимаемой им нагрузкой можно пренебречь. Сила
- 120. При расчёте ферм способом вырезания узлов все стержни, действующие на рассматриваемый узел, считают растянутыми и их
- 121. Стержни, у которых расчётные реакции имеют знак (+) работают на растяжение, а стержни, у которых расчётные
- 122. Подпятник – устройство, обеспечивающее непо- движность конца вала (как правило, вертикально -го). Сила реакции подпятника проходит
- 123. Шероховатая поверхность - поверхность, трение которой учитывают при решении задач. Сила реакции шероховатой поверхности отклонена от
- 124. В расчетах сила реакции шероховатой поверхности представляется в виде двух составляющих: силы, перпендикулярной поверхности связи (нормальной
- 125. Сила реакции невесомой гибкой нерастяжимой нити направлена от рассматриваемого тела вдоль нити к точке ее закрепления,
- 126. Жесткая заделка («заделка») - связь, обеспечива-ющая неподвижное закрепление оконечности бруса. Если на брус действует плоская система
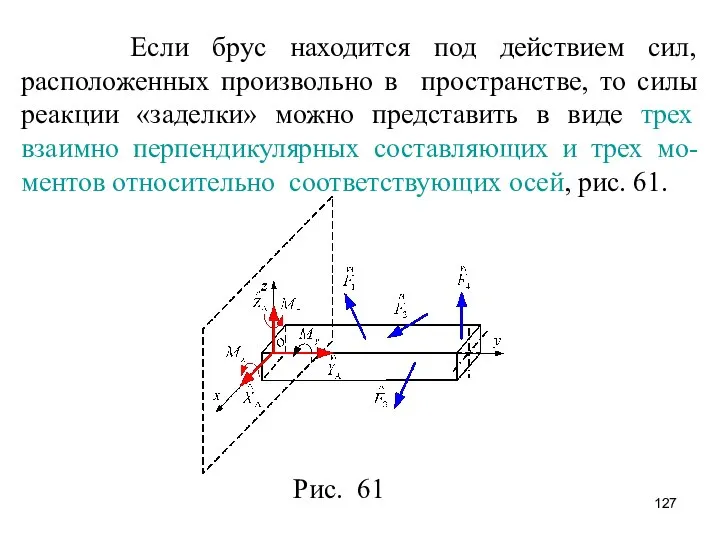
- 127. Если брус находится под действием сил, расположенных произвольно в пространстве, то силы реакции «заделки» можно представить
- 128. 7. Решение задач статики 7.1. Рекомендации по решению задач Рекомендуется придерживаться следующего плана. 1. Ознакомиться с
- 129. а) определить по условию задачи тело (узел), равно-весие которого необходимо рассмотреть, и изобразить его отдельно на
- 130. 3. Определить, какая система сил действует на рас-сматриваемое тело, и составить соответствующие ей уравнения равновесия. 4.
- 131. 8. Центр тяжести 8.1. Равнодействующая двух параллельных сил Рассмотрим две параллельные силы, приложенные в точках А1
- 135. Равнодействующая двух параллельных сил, направ-ленных в одну сторону, равна сумме этих сил:
- 136. откуда Чтобы найти положение точки приложения равно-действующей двух параллельных сил, воспользуемся теоремой Вариньона.
- 137. Применяя теорему Вариньона:
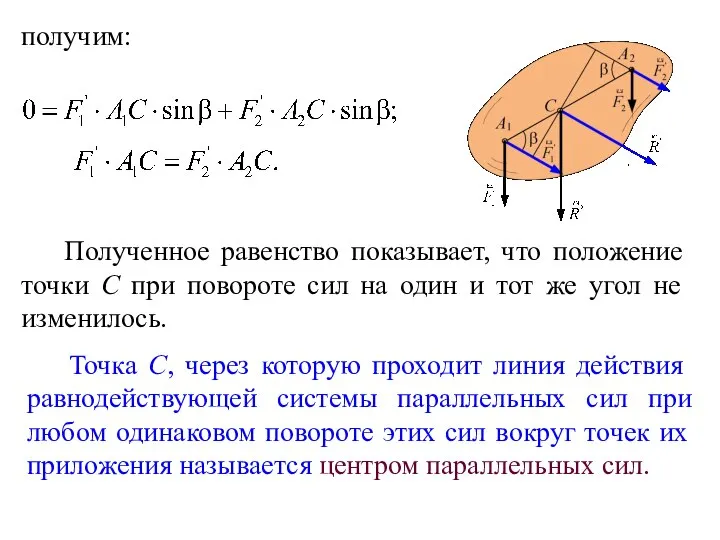
- 138. получим: Полученное равенство показывает, что положение точки С при повороте сил на один и тот же
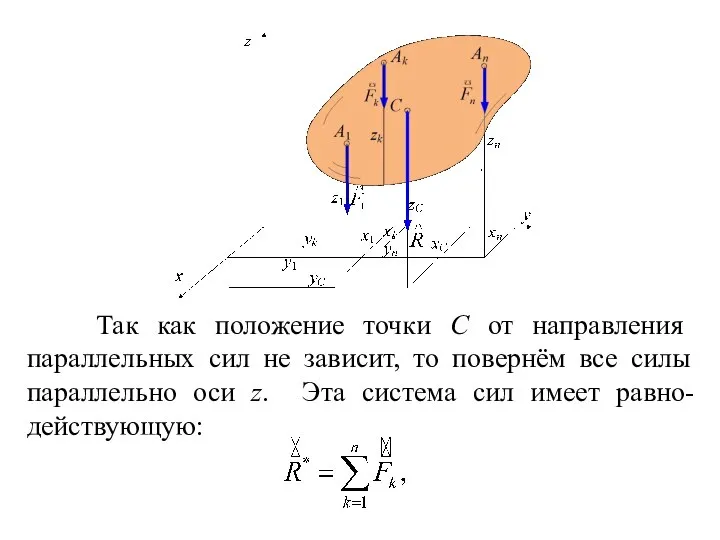
- 139. Найдём центр параллельных сил, приложенных к твёрдому телу (см. рис.). 8.2. Центр системы параллельных сил
- 140. Так как положение точки С от направления параллельных сил не зависит, то повернём все силы параллельно
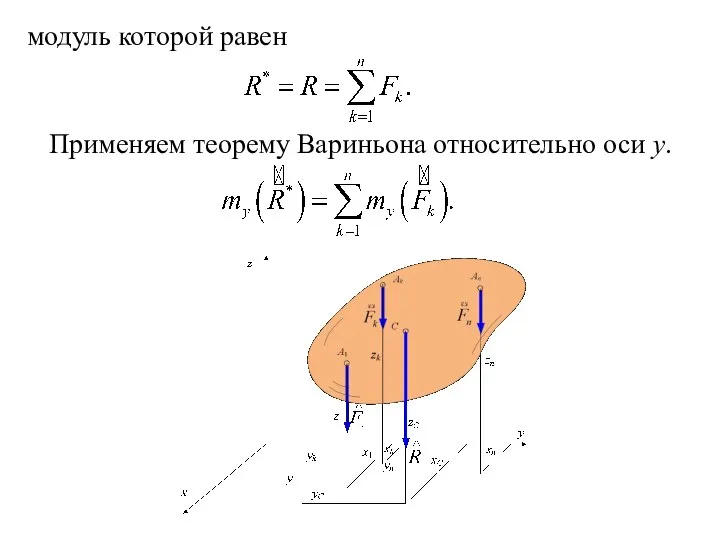
- 141. модуль которой равен Применяем теорему Вариньона относительно оси y.
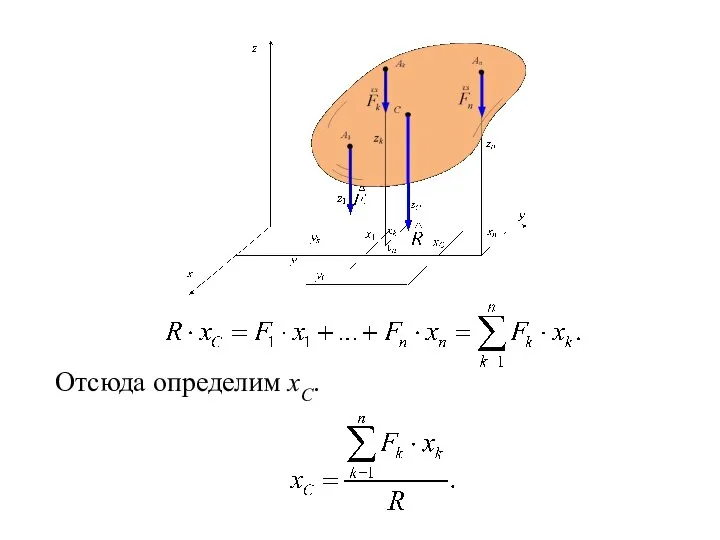
- 142. Отсюда определим xC.
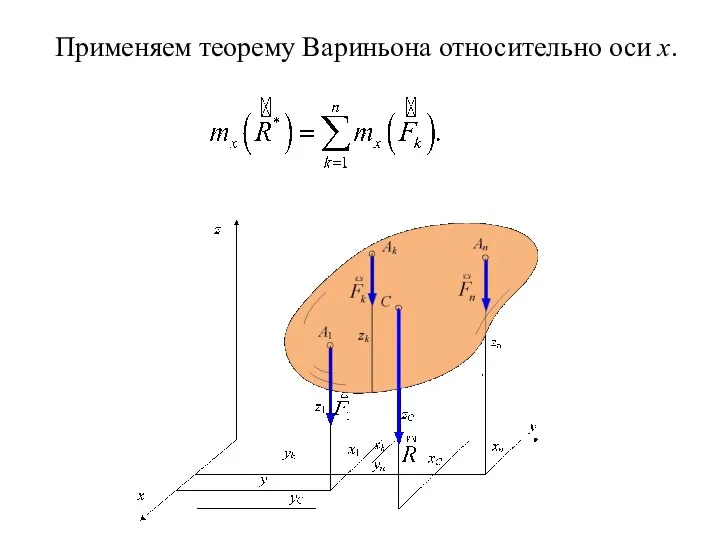
- 143. Применяем теорему Вариньона относительно оси x.
- 144. Отсюда определим yC.
- 145. Повернём силы параллельно оси y и применим теорему Вариньона относительно оси x.
- 146. Отсюда определим zC.
- 147. 8.3. Центр тяжести твёрдого тела Центром тяжести твердого тела называется неизменно связанная с этим телом точка,
- 148. Силы тяжести, действующие на каждую частицу твёрдого тела образуют систему сил, параллельных вертикальной оси z. Поэтому
- 149. Если тело является однородным, то вес pk любой его частицы пропорционален объёму vk этой части тела:
- 150. Если твёрдое тело выполнено в форме пластины, то координаты его цента тяжести определяются по формулам: где
- 151. Координаты центра тяжести линии определяются по следующим формулам: где L – длина всей линии; lk –длина
- 152. 8.4. Способы определения координат центров тяжести тел 1. Симметрия. Если однородное тело имеет плоскость, ось или
- 153. 2. Разбиение. Если тело можно разбить на конечное число таких частей, для каждой из которых положение
- 154. 3. Дополнение. Этот способ является частным случаем способа разбиения. Он применяется к телам, имеющим вырезы, если
- 155. Затем переходят к пределу, устремляя к нулю. Тогда стоящие в числителях суммы обращаются в интегралы, распространенные
- 156. Аналогично для координат центров тяжести плоского тела и весомой линии получим:
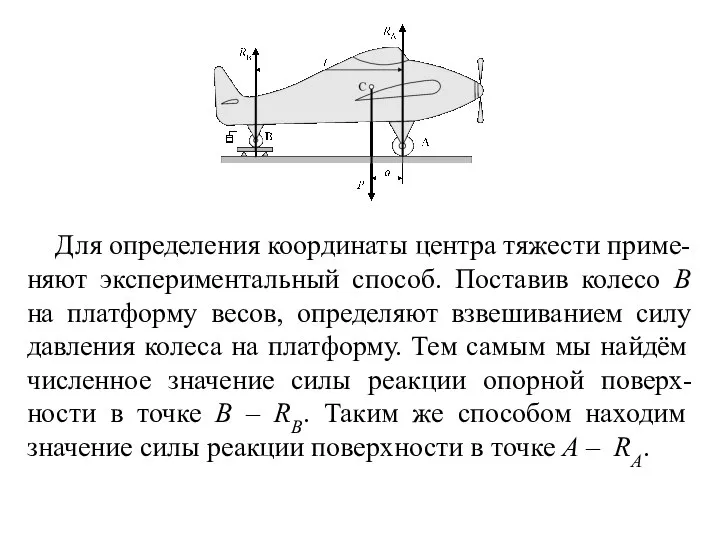
- 157. 5. Экспериментальные способы. Центры тяжести неоднородных тел сложной конфигурации можно определить экспериментально. Один из возможных экспериментальных
- 158. Для определения координаты центра тяжести приме-няют экспериментальный способ. Поставив колесо В на платформу весов, определяют взвешиванием
- 159. Применяют теорему Вариньона, в соответствии с которой сумма моментов сил относительно точки С равна нулю: откуда
- 161. Скачать презентацию













































































































































 Лептоспироз
Лептоспироз Практикум по налогам
Практикум по налогам  Многопоточное программирование. Принципы и реализация в java. (Лекция 11)
Многопоточное программирование. Принципы и реализация в java. (Лекция 11) 1204297
1204297 Автоматизированная система управления (АСУ) электроснабжением жилого дома
Автоматизированная система управления (АСУ) электроснабжением жилого дома Labor Dynamics of the IT Economy. What IT Planners Need to Know about the Nature of Programming
Labor Dynamics of the IT Economy. What IT Planners Need to Know about the Nature of Programming Политическое развитие страны в XVII веке
Политическое развитие страны в XVII веке Закон о кассовых аппаратах
Закон о кассовых аппаратах Информационные системы в менеджменте Системы Поддержки процессов Принятия Решений
Информационные системы в менеджменте Системы Поддержки процессов Принятия Решений  Презентация Содержание и психологические факторы эффективной управленческой деятельности
Презентация Содержание и психологические факторы эффективной управленческой деятельности Религия. Тотемизм
Религия. Тотемизм Обеспечение пожаровзрывобезопасности систем отопления
Обеспечение пожаровзрывобезопасности систем отопления МЕЖДУНАРОДНЫЕ ЭКОНОМИЧЕСКИЕ ОТНОШЕНИЯ ЯРОСЛАВСКОЙ ОБЛАСТИ Студент ПКФК Группа 44-БД Бызов И.О.
МЕЖДУНАРОДНЫЕ ЭКОНОМИЧЕСКИЕ ОТНОШЕНИЯ ЯРОСЛАВСКОЙ ОБЛАСТИ Студент ПКФК Группа 44-БД Бызов И.О. Норадреналин и Адреналин
Норадреналин и Адреналин Структурная схема «off-line» ИБП
Структурная схема «off-line» ИБП Учебный проект как средство активизации познавательной деятельности обучающихся
Учебный проект как средство активизации познавательной деятельности обучающихся Опалубочные работы. Опалубка
Опалубочные работы. Опалубка СОВЕРШЕНСТВОВАНИЕ ЗАКОНОДАТЕЛЬНОГО ОБЕСПЕЧЕНИЯ Проект Концепции повышения эффективности межбюджетных отношений и качества упр
СОВЕРШЕНСТВОВАНИЕ ЗАКОНОДАТЕЛЬНОГО ОБЕСПЕЧЕНИЯ Проект Концепции повышения эффективности межбюджетных отношений и качества упр Упаковка и устройства для дозированных жидких и вязких лекарственных форм
Упаковка и устройства для дозированных жидких и вязких лекарственных форм этапы секьюритизации активов
этапы секьюритизации активов  Планирование научного исследования в медицине http://prezentacija.biz/medicinskie-prezentacii/prezentacii-po-nevrologii/ Презентации по неврологии Скачать б
Планирование научного исследования в медицине http://prezentacija.biz/medicinskie-prezentacii/prezentacii-po-nevrologii/ Презентации по неврологии Скачать б МЕНЕДЖМЕНТ И ОРГАНИЗАЦИОННАЯ ДЕМОКРАТИЯ
МЕНЕДЖМЕНТ И ОРГАНИЗАЦИОННАЯ ДЕМОКРАТИЯ Прогнозирование, выявление и оценка радиационной обстановки
Прогнозирование, выявление и оценка радиационной обстановки Культурные универсалии
Культурные универсалии Рождество Христово
Рождество Христово ОРУЖИЕ ПОРАЖАЮЩЕЕ ИЗЛУЧЕНИЕМ
ОРУЖИЕ ПОРАЖАЮЩЕЕ ИЗЛУЧЕНИЕМ Этапы развития ЭВМ
Этапы развития ЭВМ  Декупаж «Лесная поляна» Выполнила: ученица 10 «А» класса МОУ СОШ №8 Минаева Наталья Магнитогорск 2011
Декупаж «Лесная поляна» Выполнила: ученица 10 «А» класса МОУ СОШ №8 Минаева Наталья Магнитогорск 2011