Содержание
- 2. Требования к статистическим оценкам Точечные оценки Интервальные оценки. Доверительные интервалы
- 3. Виды статистических оценок Статистической оценкой неизвестного параметра теоретического распределения называют функцию от наблюдаемых случайных величин. Для
- 4. Несмещенной называют статистическую оценку Θ*, математическое ожидание которой равно оцениваемому параметру Θ при любом объеме выборки,
- 5. Состоятельной называют статистическую оценку, которая при n→∞ стремится по вероятности к оцениваемому параметру. Оценки бывают точечными,
- 6. Выборочная средняя Выборочной средней называют среднее арифметическое значение признака выборочной совокупности. взвешенная средняя
- 7. Выборочная дисперсия Выборочной дисперсией называют среднее арифметическое квадратов отклонения наблюдаемых значений признака от их среднего значения
- 8. Легко «исправить» выборочную дисперсию так, чтобы её математическое ожидание было равно генеральной дисперсии. Достаточно для этого
- 9. Исправленная дисперсия является, несмещённой оценкой генеральной дисперсии. Итак, в качестве оценки генеральной дисперсии принимают исправленную дисперсию
- 10. Кроме дисперсии для характеристики рассеяния значений признака выборочной совокупности вокруг своего среднего значения пользуются сводной характеристикой
- 11. При выборке малого объема точечная оценка может разительно отличаться от оцениваемого параметра, т.е. приводить к грубым
- 12. Интервальные оценки Интервальные оценки позволяют установить точность и надежность оценок. Пусть найденная по данным выборки статистическая
- 13. Т.о., положительное число δ характеризует точность оценки. Однако, статистические методы не позволяют категорически утверждать, что оценка
- 14. Доверительный интервал Доверительным интервалом называется случайный интервал (Θ* - δ; Θ* + δ) , который покрывает
- 15. Доверительный интервал для оценки математического ожидания нормального распределения при известном среднем квадратическом отклонении t – параметр,
- 16. Смысл полученного соотношения таков: с надёжностью можно утверждать, что доверительный интервал покрывает неизвестный параметр ; точность
- 17. Доверительным вероятностям, как это видно из таблицы функции Лапласа, соответствуют следующие величины нормированных отклонений: вероятности γ
- 18. Примечание: при большом объеме выборки (n ≥ 30) значения t γ таблицы Стьюдента и t таблицы
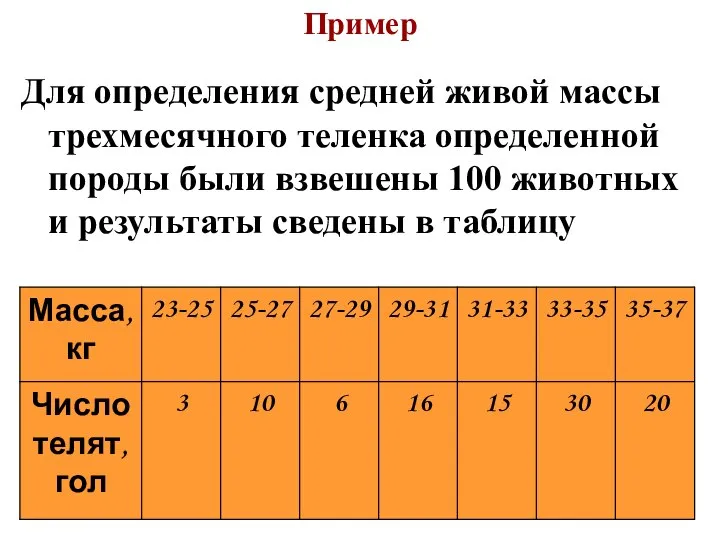
- 19. Пример Для определения средней живой массы трехмесячного теленка определенной породы были взвешены 100 животных и результаты
- 20. Найти: величины, которые следует принять за среднюю массу и среднее квадратическое отклонение; ошибку средней и коэффициент
- 21. Вычисляем выборочную исправленную дисперсию
- 22. Находим исправленное выборочное среднее квадратичное отклонение
- 23. 3) Поскольку n = 100 > 30 и у нас случай нормального распределения, то доверительный интервал
- 24. Из условия 2Φ(t γ) = 0.95 определяем Φ(t γ) = 0,475, а по таблице приложений находим
- 25. Замечание: если требуется оценить математическое ожидание с наперед заданной точностью δ и надежностью γ, то максимальный
- 26. Доверительный интервал для оценки среднего квадратического отклонения σ нормального распределения.
- 28. Скачать презентацию
























 Движения для здоровья. Влияние физических упражнений на организм
Движения для здоровья. Влияние физических упражнений на организм Технология активизации проектной деятельности
Технология активизации проектной деятельности Презентация Общевоинские уставы Вооруженных Сил РФ — закон воинской жизни
Презентация Общевоинские уставы Вооруженных Сил РФ — закон воинской жизни  Достопримечательности Китая
Достопримечательности Китая Современный подросток на приходе: что упускаем и что можем сделать
Современный подросток на приходе: что упускаем и что можем сделать Национальный японский костюм
Национальный японский костюм CУБД. Этапы проектирования. Создание таблиц, работа с данными в таблице. Построение запросов
CУБД. Этапы проектирования. Создание таблиц, работа с данными в таблице. Построение запросов Инженерный менеджмент и информационные технологии. (Лекция 1)
Инженерный менеджмент и информационные технологии. (Лекция 1) Подготовили: Порошина Л.В., Анкудинова М.А., гр.Ю-102
Подготовили: Порошина Л.В., Анкудинова М.А., гр.Ю-102  Cherrikita. Что же это за канал?
Cherrikita. Что же это за канал? Залоговое право и поручительство в практике верховного суда РФ
Залоговое право и поручительство в практике верховного суда РФ Русские народные традиции и обряды. (Часть 1)
Русские народные традиции и обряды. (Часть 1) Дискуссия об английском артикле: перспектива и ретроспектива
Дискуссия об английском артикле: перспектива и ретроспектива Банковский менеджмент (1)
Банковский менеджмент (1) Наука и философия
Наука и философия Технология получения электронной аппаратуры для работы в условиях экстремальных ударных нагрузок
Технология получения электронной аппаратуры для работы в условиях экстремальных ударных нагрузок Без названия
Без названия ФИАТНЫЕ деньги Петрова М.А.
ФИАТНЫЕ деньги Петрова М.А. Художественные системы в проектировании одежды
Художественные системы в проектировании одежды Ангелы. Представления об ангелах в исламе
Ангелы. Представления об ангелах в исламе Штриховой код - штрих-ко́д
Штриховой код - штрих-ко́д  Оlimpic Champion in Ukraine
Оlimpic Champion in Ukraine Защита авторских прав на контент
Защита авторских прав на контент Строение зрительного анализатора.
Строение зрительного анализатора. Презентация на тему "Восковые моделировочные материалы применяемые в клинике ортопедической стоматологии (+)" - скачать презе
Презентация на тему "Восковые моделировочные материалы применяемые в клинике ортопедической стоматологии (+)" - скачать презе Введение в теорию оптимизации. Лекция1
Введение в теорию оптимизации. Лекция1 Презентация Значение теории относительности Эйнштейна
Презентация Значение теории относительности Эйнштейна Замісник (проксі). Патерни проектування
Замісник (проксі). Патерни проектування